Gelöste Aufgaben/Kw56: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 9: | Zeile 9: | ||
==Aufgabenstellung== | ==Aufgabenstellung== | ||
Die Aufgabenstellung ist identisch mit Aufgabe Kw55, hier ist die Lösung mit dem Verfahren von [[Randwertprobleme/Methoden zur Lösung von Randwertproblemen/Verfahren von Rayleigh-Ritz (EBB)|Rayleigh-Ritz]] gefragt. | |||
<onlyinclude> | <onlyinclude> | ||
[[Datei:Kw55-01.png|alternativtext=|links|mini|250x250px|Lageplan]] | [[Datei:Kw55-01.png|alternativtext=|links|mini|250x250px|Lageplan]] | ||
Gesucht ist | Gesucht ist eine Näherungslösung mit dem [[Randwertprobleme/Methoden zur Lösung von Randwertproblemen/Verfahren von Rayleigh-Ritz (EBB)|Verfahren von Rayleigh-Ritz]] für ein [[Sources/Lexikon/Euler-Bernoulli-Balken|Euler-Bernoulli-Modell]] der Struktur. | ||
</onlyinclude> | </onlyinclude> | ||
Verwenden Sie zwei freie [[Sources/Lexikon/Trial-Function|Trial-Funtions]]. | |||
== Lösung mit Maxima == | == Lösung mit Maxima == | ||
==tmp== | |||
Die Herausforderung der Aufgabe liegt wieder in der kinematischen Zwangsbedingung, die der starre Stab ''abc'' dem Euler-Bernoulli-Balken auferlegt. Diese Zwangsbedingung lautet | |||
<math>w_B = \displaystyle \frac{1}{2} w_C</math>, | |||
mit den Abkürzungen | |||
* ''w<sub>B</sub> = w( ℓ),'' | |||
* ''''w<sub>C</sub>= w(2ℓ).'''' | |||
Die geometrischen Randbedingungen in A erfüllen wir, indem wir Polynome ab dem Grad 2 verwenden. | |||
Für die Lösung nach Rayleigh-Ritz können wir | |||
* zwei freie Trial-Functions wählen, die die Zwangsbedingung selbst schon erfüllen | |||
* mit [https://de.wikipedia.org/wiki/Lagrange-Multiplikator Lagrange-Multiplikator] die Zwangsbedingung einbauen. | |||
Der zweite Weg ist bei Computer-Anwendungen meist viel einfacher - den gehen wir hier. | |||
<!--------------------------------------------------------------------------------> | <!--------------------------------------------------------------------------------> | ||
{{MyCodeBlock|title=Header | {{MyCodeBlock|title=Header | ||
|text=Text | |text=Text | ||
| Zeile 30: | Zeile 48: | ||
==tmp== | ==tmp== | ||
<!--------------------------------------------------------------------------------> | Wir brauchen | ||
<math>q_0 = \displaystyle \frac{m\,g}{\ell}</math> | |||
und nutzen eine Referenzlösung (wie in Kw55) | |||
<math>\begin{array}{ccc} | |||
\hat{w} &=& \displaystyle \frac{q_0\,(2\ell)^4}{8 EI}\\ | |||
\hat{\phi}&=& \displaystyle \frac{q_0\,(2\ell)^3}{6 EI} | |||
\end{array}</math>.<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Declarations | {{MyCodeBlock|title=Declarations | ||
|text=Text | |text=Text | ||
| Zeile 40: | Zeile 68: | ||
==tmp== | ==tmp== | ||
Um zwei freie Trial-Functions zu bekommen, müssen wir drei ansetzen: ein Freiheitsgrad wird von der kinematischen Zwangsbedingung aufgehoben. | |||
Also wählen wir | |||
<math>\displaystyle w(\xi) = \hat{w} \cdot \sum_{i=2}^4 W_i \cdot \xi^i</math> | |||
mit | |||
<math>x = \xi \cdot \ell</math> | |||
und ergänzen dies um die Zwangsbedingung | |||
<math>2\cdot w(1) = \,w(2)</math>. | |||
Achtung: Der Balken ist "2"-lang. | |||
<!--------------------------------------------------------------------------------> | <!--------------------------------------------------------------------------------> | ||
{{MyCodeBlock|title=Formfunctions | {{MyCodeBlock|title=Formfunctions | ||
|text=Text | |text=Text | ||
| Zeile 50: | Zeile 95: | ||
==tmp== | ==tmp== | ||
Für die Gleichgewichtsbedingungen brauchen wir die potentielle Energie (hier die Lagrange-Funktion) | |||
<math>\begin{array}{lcl} | |||
\Lambda = & &\displaystyle \frac{1}{2\cdot \ell^3}\displaystyle EI \int_{0}^{2}\left( \displaystyle \frac{d^2}{d\,\xi^2} \cdot w(\xi) \right)^{2} d\xi\\ | |||
&-&\left(2 m\,g+\displaystyle \frac{1}{2} m\,g\right) \cdot w(1)+\left(\displaystyle \frac{1}{2} m\,g\right)\cdot w(2)\\ | |||
&+&\lambda \cdot \displaystyle \frac{m^2\,g^2 \ell^3}{EI}\cdot (2\,w(1)- w(2)) | |||
\end{array}</math> | |||
wobei der konstante Faktor bei dem [https://de.wikipedia.org/wiki/Lagrange-Multiplikator Lagrange-Multiplikator] ''λ'' nur der Ästhetik dient .... | |||
Die gesuchten Größen sind nun | |||
<math>\underline{Q} = \left( \begin{array}{c} | |||
W_2\\ | |||
W_3\\ | |||
W_4\\ | |||
\lambda | |||
\end{array}\right)</math>, | |||
und die Gleichgewichtsbedingungen kommen aus | |||
<math>\displaystyle \frac{d\Lambda}{dQ_i} \stackrel{!}{=}0</math> | |||
zu | |||
<math>\begin{array}{cc} | |||
-2 \lambda +256 {W_4}+96 {W_3}+32 {W_2}-1&=0,\\ | |||
-2 \lambda +384 {W_4}+128 {W_3}+32 {W_2}+1&=0,\\ | |||
70 \lambda -18432 {W_4}-5760 {W_3}-1280 {W_2}-55&=0,\\ | |||
-7 {W_4}-3 {W_3}-{W_2}&=0 | |||
\end{array}</math>. | |||
<!--------------------------------------------------------------------------------> | <!--------------------------------------------------------------------------------> | ||
{{MyCodeBlock|title=Equilibrium Conditions | {{MyCodeBlock|title=Equilibrium Conditions | ||
|text=Text | |text=Text | ||
| Zeile 60: | Zeile 139: | ||
==tmp== | ==tmp== | ||
Dieses lineare Gleichungssystem hat die Lösung | |||
<math>\displaystyle {{W}_{2}}=\frac{23}{56},{{W}_{3}}=-\frac{27}{112},{{W}_{4}}=\frac{5}{112},\lambda=\frac{3}{14}</math> | |||
<!--------------------------------------------------------------------------------> | <!--------------------------------------------------------------------------------> | ||
{{MyCodeBlock|title=Solving | {{MyCodeBlock|title=Solving | ||
|text=Text | |text=Text | ||
| Zeile 70: | Zeile 153: | ||
==tmp== | ==tmp== | ||
[[Datei:Kw56-21.png|mini|Verläufe der gesuchten Größen]] | [[Datei:Kw56-21.png|mini|Verläufe der gesuchten Größen|alternativtext=|ohne]] | ||
Einsetzen in die Trial-Functions liefert die (dimensionslosen) Funktionsverläufe für ''w, ϕ, M'' und ''Q'': | |||
<!--------------------------------------------------------------------------------> | <!--------------------------------------------------------------------------------> | ||
{{MyCodeBlock|title=Post-Processing | {{MyCodeBlock|title=Post-Processing | ||
Version vom 31. März 2021, 08:09 Uhr
Aufgabenstellung
Die Aufgabenstellung ist identisch mit Aufgabe Kw55, hier ist die Lösung mit dem Verfahren von Rayleigh-Ritz gefragt.
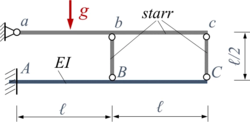
Gesucht ist eine Näherungslösung mit dem Verfahren von Rayleigh-Ritz für ein Euler-Bernoulli-Modell der Struktur.
Verwenden Sie zwei freie Trial-Funtions.
Lösung mit Maxima
tmp
Die Herausforderung der Aufgabe liegt wieder in der kinematischen Zwangsbedingung, die der starre Stab abc dem Euler-Bernoulli-Balken auferlegt. Diese Zwangsbedingung lautet
,
mit den Abkürzungen
- wB = w( ℓ),
- 'wC= w(2ℓ).'
Die geometrischen Randbedingungen in A erfüllen wir, indem wir Polynome ab dem Grad 2 verwenden.
Für die Lösung nach Rayleigh-Ritz können wir
- zwei freie Trial-Functions wählen, die die Zwangsbedingung selbst schon erfüllen
- mit Lagrange-Multiplikator die Zwangsbedingung einbauen.
Der zweite Weg ist bei Computer-Anwendungen meist viel einfacher - den gehen wir hier.
Header
Text
1+1
tmp
Wir brauchen
und nutzen eine Referenzlösung (wie in Kw55)
.
Declarations
Text
1+1
tmp
Um zwei freie Trial-Functions zu bekommen, müssen wir drei ansetzen: ein Freiheitsgrad wird von der kinematischen Zwangsbedingung aufgehoben.
Also wählen wir
mit
und ergänzen dies um die Zwangsbedingung
.
Achtung: Der Balken ist "2"-lang.
Formfunctions
Text
1+1
tmp
Für die Gleichgewichtsbedingungen brauchen wir die potentielle Energie (hier die Lagrange-Funktion)
wobei der konstante Faktor bei dem Lagrange-Multiplikator λ nur der Ästhetik dient ....
Die gesuchten Größen sind nun
,
und die Gleichgewichtsbedingungen kommen aus
zu
.
Equilibrium Conditions
Text
1+1
tmp
Dieses lineare Gleichungssystem hat die Lösung
Solving
Text
1+1
tmp
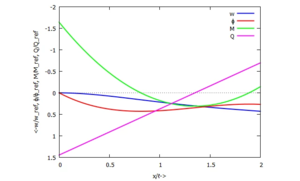
Einsetzen in die Trial-Functions liefert die (dimensionslosen) Funktionsverläufe für w, ϕ, M und Q:
Post-Processing
Text
1+1
Links
- ...
Literature
- ...