Gelöste Aufgaben/Kw55: Unterschied zwischen den Versionen
| Zeile 24: | Zeile 24: | ||
* ''w<sub>B</sub>'' = w( ℓ) | * ''w<sub>B</sub>'' = w( ℓ) | ||
* '<nowiki/>'' | *''w''<nowiki/>''<sub>C</sub>''='''<nowiki/>''' '''<nowiki/>'''w(2ℓ) | ||
Wir schneiden beide Systemteile frei: | Wir schneiden beide Systemteile frei: | ||
| Zeile 44: | Zeile 44: | ||
ein, die zunächst unbekannt sind. Wir müssen überlegen, wo wir Bedingungen für diese beiden Größen herbekommen. | ein, die zunächst unbekannt sind. Wir müssen überlegen, wo wir Bedingungen für diese beiden Größen herbekommen. | ||
Die Lösung der Teilaufgabe für den Euler-Bernoulli-Balken ist ein klassisches Randwertproblem mit | Die Lösung der Teilaufgabe für den [[Sources/Lexikon/Euler-Bernoulli-Balken|Euler-Bernoulli-Balken]] ist ein klassisches Randwertproblem mit | ||
<ol> | <ol> | ||
| Zeile 62: | Zeile 62: | ||
</td></tr> | </td></tr> | ||
</table> | </table> | ||
Zusätzlich zum "klassischen" Randwertproblem haben wir hier eine geometrische Zwangsbedingung durch die starren Stäbe. | Zusätzlich zum "klassischen" Randwertproblem haben wir hier eine geometrische Zwangsbedingung durch die starren Stäbe. | ||
==tmp== | ==tmp== | ||
In dieser Lösung arbeiten wir mit dimensionslosen Koordinaten für die unabhängige Koordinate ''x'' und die abhängige Koordinate ''w(x)''. | |||
<!--------------------------------------------------------------------------------> | <!--------------------------------------------------------------------------------> | ||
{{MyCodeBlock|title=Header | {{MyCodeBlock|title=Header | ||
|text=Text | |text=Text | ||
| Zeile 77: | Zeile 78: | ||
==tmp== | ==tmp== | ||
<!--------------------------------------------------------------------------------> | Die Streckenlast auf den Balken ist natürlich seine Gewichtskraft, also | ||
<math>\displaystyle q_0 = \frac{m\;g}{\ell}</math>. | |||
Später werden wir noch die dimensionslose Koordinate | |||
<math>\xi = \displaystyle \frac{x}{\ell}</math> | |||
gebrauchen.<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Declarations | {{MyCodeBlock|title=Declarations | ||
|text=Text | |text=Text | ||
| Zeile 87: | Zeile 97: | ||
==tmp== | ==tmp== | ||
<!--------------------------------------------------------------------------------> | In Bereich I und II gilt dieselbe Bewegungs-Differentialgleichung | ||
<math>E\,I\, w_i^{IV}(x) = q_0 ,\;\; i=\{1,2\}</math>, | |||
die wir durch Integration lösen und dann bereichsweise an Rand- und Übergangsbedingungen anpassen. Die Bedeutung der gesuchten Auslenkung ''w'' und seiner Ableitungen sind | |||
<math>\begin{array}{ll} \ldots\text{ die Auslenkung: }&\displaystyle w_i(x) \\\ldots\text{ die Verdrehung: }&\displaystyle \phi_i(x) = \frac{d\,w_i(x)}{d\,x}\\ \ldots\text{ das Biege-Moment: }&\displaystyle M_i(x) = - E I \frac{d^2\,w_i(x)}{d\,x^2}\\ \ldots\text{ die Querkraft: }&\displaystyle Q_i(x) = - EI \frac{d^3\,w_i(x)}{d\,x^3} \end{array}</math> | |||
Wir finden wir für Bereich ''i'': | |||
<math>\begin{array}{rcl} | |||
EI \cdot w_i( x) &:=&\displaystyle \frac{{q_0}\, {{x}^{4}}}{24}+\frac{{C_{2,3}}\, {{x}^{3}}}{6}+\frac{{C_{2,2}}\, {{x}^{2}}}{2}+{C_{2,1}} x+{C_{2,0}}\\ | |||
EI \cdot \phi_i( x) &:=&\displaystyle \frac{{q_0}\, {{x}^{3}}}{6}+\frac{{C_{2,3}}\, {{x}^{2}}}{2}+{C_{2,2}} x+{C_{2,1}} \\ | |||
M_i(x) &:=&\displaystyle -\frac{{q_0}\, {{x}^{2}}}{2}-{C_{2,3}} x-{C_{2,2}}\\ | |||
Q_i(x) &:=&\displaystyle -{q_0} x-{C_{2,3}}\\ | |||
\end{array}</math>.<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Integration Of Differential Equation | {{MyCodeBlock|title=Integration Of Differential Equation | ||
|text=Text | |text=Text | ||
| Zeile 97: | Zeile 123: | ||
==tmp== | ==tmp== | ||
Für die 2*4 = 8 Integrationskonstanten | |||
<math>\left[ C_{1,0},C_{1,1},C_{1,2},C_{1,3},C_{2,0},C_{2,1},C_{2,2},C_{2,3}\right]</math> | |||
suchen wir jetzt die passenden Gleichungen aus Rand- und Übergangsbedingungen. Und zusätzlich - und das ist hier besonders - brauchen wir noch je eine Gleichung für die Stabkräfte ''F<sub>B</sub>'' und ''F<sub>C</sub>''. | |||
Zur besseren Übersicht nennen wir die Schnitt-Momente und -Kräfte nach den jeweiligen Knotenpunkten ''A, B, C'' und fügen als Index ein + / - hinzu, um die Seite (+: rechts vom Knoten, -: links vom Knoten) zu kennzeichnen. | |||
Die Normalkräfte ''N'' brauchen wir dabei nicht auszuwerten. | |||
====Aus Rand "A"==== | ====Aus Rand "A"==== | ||
| Zeile 162: | Zeile 197: | ||
==tmp== | ==tmp== | ||
Das Gleichungssystem wollen wir als | |||
<math>\underline{\underline{A}}\cdot\underline{X}= \underline{b}</math> | |||
schreiben, also - hier nach Einsetzen der System-Parameter: | |||
<math>\begin{pmatrix}1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ | |||
0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ | |||
1 & \ell & \frac{{{\ell}^{2}}}{2} & \frac{{{\ell}^{3}}}{6} & -1 & -\ell & -\frac{{{\ell}^{2}}}{2} & -\frac{{{\ell}^{3}}}{6} & 0 & 0\\ | |||
0 & 1 & \ell & \frac{{{\ell}^{2}}}{2} & 0 & -1 & -\ell & -\frac{{{\ell}^{2}}}{2} & 0 & 0\\ | |||
0 & 0 & 0 & 1 & 0 & 0 & 0 & -1 & -1 & 0\\ | |||
0 & 0 & 1 & \ell & 0 & 0 & -1 & -\ell & 0 & 0\\ | |||
0 & 0 & 0 & 0 & 0 & 0 & -1 & -2 \ell & 0 & 0\\ | |||
0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & -1\\ | |||
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 2\\ | |||
1 & \ell & \frac{{{\ell}^{2}}}{2} & \frac{{{\ell}^{3}}}{6} & -\frac{1}{2} & -\ell & -{{\ell}^{2}} & -\frac{2 {{\ell}^{3}}}{3} & 0 & 0\end{pmatrix} \cdot \begin{pmatrix}{C_{1,0}}\\ | |||
{C_{1,1}}\\ | |||
{C_{1,2}}\\ | |||
{C_{1,3}}\\ | |||
{C_{2,0}}\\ | |||
{C_{2,1}}\\ | |||
{C_{2,2}}\\ | |||
{C_{2,3}}\\ | |||
{F_B}\\ | |||
{F_C}\end{pmatrix} = m g \cdot \begin{pmatrix}0\\ | |||
0\\ | |||
0\\ | |||
0\\ | |||
0\\ | |||
0\\ | |||
2 \ell\\ | |||
-2\\ | |||
\displaystyle -\frac{7}{2}\\ | |||
\displaystyle \frac{7 {{\ell}^{3}}}{24}\end{pmatrix}</math> | |||
<!--------------------------------------------------------------------------------> | <!--------------------------------------------------------------------------------> | ||
{{MyCodeBlock|title=Prepare for Solver | {{MyCodeBlock|title=Prepare for Solver | ||
|text=Text | |text=Text | ||
| Zeile 172: | Zeile 242: | ||
==tmp== | ==tmp== | ||
Das Lösen des Gleichungssystems liefert dann | |||
<math>\displaystyle \left( \begin{array}{c} C_{1,0}\\C_{1,1}\\C_{1,2}\\C_{1,3}\\C_{2,0}\\C_{2,1}\\C_{2,2}\\C_{2,3}\\F_B\\F_C \end{array}\right) = m\; g \cdot \left(\begin{array}{c} | |||
0\\ | |||
0\\ | |||
\displaystyle \frac{11 \ell}{2}\\ | |||
\displaystyle -\frac{29}{4}\\ | |||
\displaystyle -\frac{7 {{\ell}^{3}}}{6}\\ | |||
\displaystyle \frac{7 {{\ell}^{2}}}{2}\\ | |||
\displaystyle -\frac{3 \ell}{2}\\ | |||
\displaystyle -\frac{1}{4}\\ | |||
-7\\ | |||
\displaystyle \frac{7}{4} | |||
\end{array} \right)</math>. | |||
<!--------------------------------------------------------------------------------> | <!--------------------------------------------------------------------------------> | ||
{{MyCodeBlock|title=Solving | {{MyCodeBlock|title=Solving | ||
|text=Text | |text=Text | ||
| Zeile 182: | Zeile 268: | ||
==tmp== | ==tmp== | ||
<!--------------------------------------------------------------------------------> | Die Ergebnisse plotten wir und nutzen dafür als Referenzgrößen die Standard-Lösungen für den Kragbalken unter Streckenlast mit | ||
* <math>\displaystyle w_{ref} = \frac{q_0 \cdot (2 \ell)^4}{8} </math> und | |||
* <math>\displaystyle \phi_{ref} = \frac{q_0 \cdot (2 \ell)^3}{6}</math>. | |||
Damit sehen die Ergebnisse so aus ... | |||
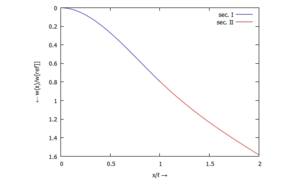
====... für w(x): ==== | |||
[[Datei:Kw50-21.png|mini|Biegelinie ''w(x)''|alternativtext=|ohne]] | |||
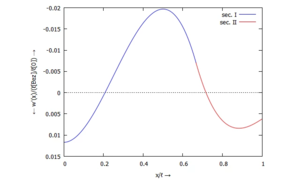
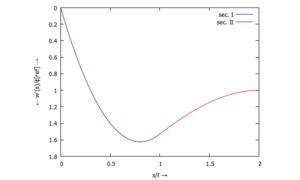
====... für ''Φ(x)'':==== | |||
[[Datei:Kw50-22.png|mini|Kippung ''w'(x)''|alternativtext=|ohne]] | |||
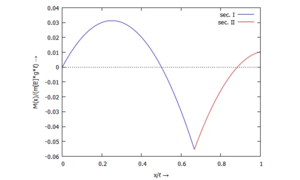
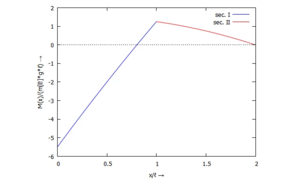
====... für M(x):==== | |||
[[Datei:Kw50-23.png|mini|Biegemoment M(x)|alternativtext=|ohne]] | |||
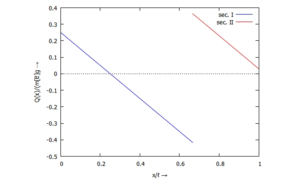
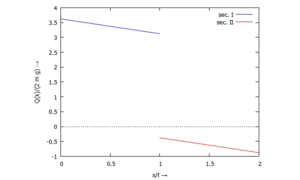
====... für Q(x):==== | |||
[[Datei:Kw50-24.png|mini|Querkraft ''Q(x)''|alternativtext=|ohne]]<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Post-Processing | {{MyCodeBlock|title=Post-Processing | ||
|text=Text | |text=Text | ||
Version vom 31. März 2021, 07:41 Uhr
Aufgabenstellung
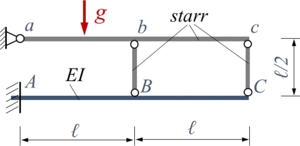
Die parallelen Stäbe ABC und abc haben je die Länge 2ℓ. Sie sind jeweils in b-B und c-C gelenkig mit einem vertikalen Stab verbunden. Die Stäbe abc, bB und cC sind starr, Stab ABC hat die Biegesteifigkeit EI. Alle Stäbe haben eine Masse m je Länge ℓ, die Erdbeschleunigung ist g.
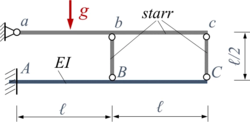
Gesucht ist die analytische Lösung für ein Euler-Bernoulli-Modell der Struktur.
Wir lösen das Gleichungssystem zur Bestimmung der Integrationskonstanten der Differentialgleichung des Euler-Bernoulli-Balkens und geben die grafischen Lösungen für w, w', M und Q an.
Gegeben: ℓ, EI, m, g
Lösung mit Maxima
Das System besteht aus den drei starren Stäben und dem elastischen Balken.
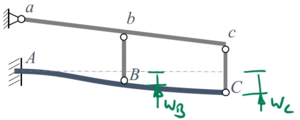
Die Verschiebungen und Verbiegungen der Stäbe verstehen wir am besten, wenn wir uns das System einmal im ausgelenkten Zustand ansehen. Gleichgewichtsbedingungen für das starre System erhalten wir einfach wie in TM-1 aus einer Momentenbilanz um A, die Gleichgewichtsbedingungen für den Euler-Bernoulli-Balken ist die Feld-Differentialgleichung, deren Integrationsbedingungen wir aus den Randbedingungen erhalten.
Die Auslenkungen des Balkens in B und C bezeichnen wir mit
- wB = w( ℓ)
- wC= w(2ℓ)
Wir schneiden beide Systemteile frei:
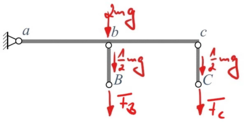
|
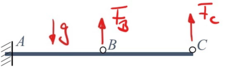
|
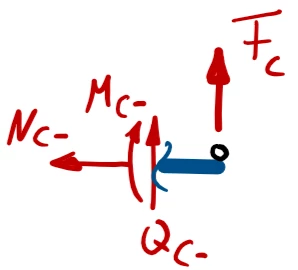
Als Schnittkräfte führen wir die beiden Stabkräfte
- FB und
- FC
ein, die zunächst unbekannt sind. Wir müssen überlegen, wo wir Bedingungen für diese beiden Größen herbekommen.
Die Lösung der Teilaufgabe für den Euler-Bernoulli-Balken ist ein klassisches Randwertproblem mit
- zwei Gebieten, in denen ein Euler-Bernoulli-Balken in AB und BC durch eine Streckenlast q0 belastet ist und somit durch die Differentialbeziehung
- beschrieben wird;
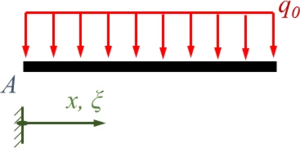
- Rand- und Übergangsbedingungen in den Punkten A, B, C.
Die Biegesteifigkeit des Balkens ist konstant (also nicht von "x" abhängig), wir können als den Index "i" beim Flächenmoment also weglassen.
Wir verwenden ein x bzw. ξ als Koordinaten in beiden Gebieten, in der Übersicht sieht das Randwertproblem mit Kraft-Randbedingungen also so aus:
| Rand A | Bereich I | Übergang B | Bereich II | Rand C |
|---|---|---|---|---|
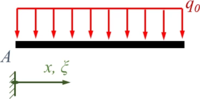 | 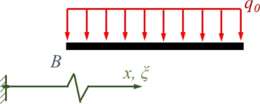 | |||
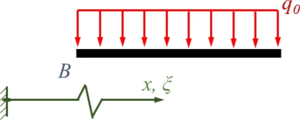
| nur "geometrische" Randbedingungen. | 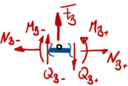 | 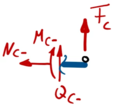
|
Zusätzlich zum "klassischen" Randwertproblem haben wir hier eine geometrische Zwangsbedingung durch die starren Stäbe.
tmp
In dieser Lösung arbeiten wir mit dimensionslosen Koordinaten für die unabhängige Koordinate x und die abhängige Koordinate w(x).
Header
Text
1+1
tmp
Die Streckenlast auf den Balken ist natürlich seine Gewichtskraft, also
.
Später werden wir noch die dimensionslose Koordinate
gebrauchen.
Declarations
Text
1+1
tmp
In Bereich I und II gilt dieselbe Bewegungs-Differentialgleichung
,
die wir durch Integration lösen und dann bereichsweise an Rand- und Übergangsbedingungen anpassen. Die Bedeutung der gesuchten Auslenkung w und seiner Ableitungen sind
Wir finden wir für Bereich i:
.
Integration Of Differential Equation
Text
1+1
tmp
Für die 2*4 = 8 Integrationskonstanten
suchen wir jetzt die passenden Gleichungen aus Rand- und Übergangsbedingungen. Und zusätzlich - und das ist hier besonders - brauchen wir noch je eine Gleichung für die Stabkräfte FB und FC.
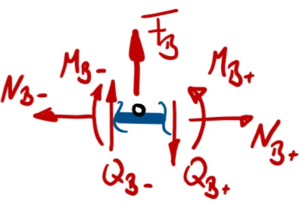
Zur besseren Übersicht nennen wir die Schnitt-Momente und -Kräfte nach den jeweiligen Knotenpunkten A, B, C und fügen als Index ein + / - hinzu, um die Seite (+: rechts vom Knoten, -: links vom Knoten) zu kennzeichnen.
Die Normalkräfte N brauchen wir dabei nicht auszuwerten.
Aus Rand "A"
| Geometrische Randbedingungen
Kraft- und Momenten-Randbedingungen
|
Aus Übergang "B"
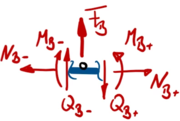
| Geometrische Randbedingungen
Kraft- und Momenten-Randbedingungen |
Aus Rand "C"
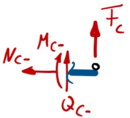
| Geometrische RandbedingungenKraft- und Momenten-Randbedingungen |
Aus Rand a (Gelenk-Lager in a)
| Momentengleichgewicht Für de starren Stäbe stellen wir die Summe aller Momente um "a" auf: Kinemtische Verträglichkeit |
Ein bisschen exotisch ist, dass wir nun zehn Unbekannte haben, nämlich
Aber mit den Randbedingungen oben steht uns nun ein vollständiges Gleichungssystem für diese zehn Unbekannten - die Integrationskonstanten und die Stabkräfte - zur Verfügung.
Boundary Conditions
Text
1+1
tmp
Das Gleichungssystem wollen wir als
schreiben, also - hier nach Einsetzen der System-Parameter:
Prepare for Solver
Text
1+1
tmp
Das Lösen des Gleichungssystems liefert dann
.
Solving
Text
1+1
tmp
Die Ergebnisse plotten wir und nutzen dafür als Referenzgrößen die Standard-Lösungen für den Kragbalken unter Streckenlast mit
- und
- .
Damit sehen die Ergebnisse so aus ...
... für w(x):
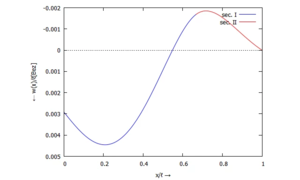
... für Φ(x):
... für M(x):
... für Q(x):
Post-Processing
Text
1+1
Links
- ...
Literature
- ...