Gelöste Aufgaben/Kw52: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
|||
| Zeile 37: | Zeile 37: | ||
==tmp== | ==tmp== | ||
Wir arbeiten mit den selben Parametern und Bezugslängen, wie in [[Gelöste Aufgaben/Kw50|Kw50]]. | |||
<!--------------------------------------------------------------------------------> | <!--------------------------------------------------------------------------------> | ||
{{MyCodeBlock|title=Declarations | {{MyCodeBlock|title=Declarations | ||
|text=Text | |text=Text | ||
| Zeile 47: | Zeile 49: | ||
==tmp== | ==tmp== | ||
<!--------------------------------------------------------------------------------> | Wir nutzen zwei Finite Elemente für die Brücke und setzen dafür die klassischen Hermite-Polynome, i.e. Polynome dritten Grades, an. | ||
An den drei Knotenpunkten ''A, B'' und ''C'' haben wir also zusammen die Koordinaten | |||
<math>\underline{Q} = \left( \begin{array}{c} W_A\\ \Phi_A \\ W_B\\ \Phi_B \\W_C\\ \Phi_C\end{array} \right)</math>.<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Formfunctions | {{MyCodeBlock|title=Formfunctions | ||
|text=Text | |text=Text | ||
| Zeile 57: | Zeile 64: | ||
==tmp== | ==tmp== | ||
<!--------------------------------------------------------------------------------> | Für die Gleichgewichtsbedingung | ||
<math>\begin{array}{lll}\delta W&=&\delta W^a - \delta\Pi\\&\stackrel{!}{=}&0\end{array}</math> | |||
konstruieren wir - ohne Berücksichtung der geometrischen Zwangsbedingungen - | |||
<math>\delta\Pi = \delta\underline{Q}^T \cdot \underline{\underline{K}}_0 \cdot \underline{Q} + K_C\; \Phi_C \; \delta\Phi_C</math> | |||
mit | |||
<math>\underline{\underline{K}}_0 = EI \cdot \begin{pmatrix}\frac{12}{{{\ell}_{1}^{3}}} & \frac{6}{{{\ell}_{1}^{2}}} & -\frac{12}{{{\ell}_{1}^{3}}} & \frac{6}{{{\ell}_{1}^{2}}} & 0 & 0\\ \frac{6}{{{\ell}_{1}^{2}}} & \frac{4}{{\ell_1}} & -\frac{6}{{{\ell}_{1}^{2}}} & \frac{2}{{\ell_1}} & 0 & 0\\ -\frac{12}{{{\ell}_{1}^{3}}} & -\frac{6}{{{\ell}_{1}^{2}}} & \frac{12 {{\ell}_{2}^{3}}+12 {{\ell}_{1}^{3}}}{{{\ell}_{1}^{3}}\, {{\ell}_{2}^{3}}} & -\frac{6 {{\ell}_{2}^{2}}-6 {{\ell}_{1}^{2}}}{{{\ell}_{1}^{2}}\, {{\ell}_{2}^{2}}} & -\frac{12}{{{\ell}_{2}^{3}}} & \frac{6}{{{\ell}_{2}^{2}}}\\ \frac{6}{{{\ell}_{1}^{2}}} & \frac{2}{{\ell_1}} & -\frac{6 {{\ell}_{2}^{2}}-6 {{\ell}_{1}^{2}}}{{{\ell}_{1}^{2}}\, {{\ell}_{2}^{2}}} & \frac{4 {\ell_2}+4 {\ell_1}}{{\ell_1}\, {\ell_2}} & -\frac{6}{{{\ell}_{2}^{2}}} & \frac{2}{{\ell_2}}\\ 0 & 0 & -\frac{12}{{{\ell}_{2}^{3}}} & -\frac{6}{{{\ell}_{2}^{2}}} & \frac{12}{{{\ell}_{2}^{3}}} & -\frac{6}{{{\ell}_{2}^{2}}}\\ 0 & 0 & \frac{6}{{{\ell}_{2}^{2}}} & \frac{2}{{\ell_2}} & -\frac{6}{{{\ell}_{2}^{2}}} & \frac{4}{{\ell_2}}\end{pmatrix}</math> | |||
und | |||
<math>\delta W^a = \delta\underline{Q}^T \cdot \underline{P}_0 + m_A\,g\; W_A \; \delta W_A</math> | |||
mit | |||
<math>\displaystyle \underline{P}_0 = \frac{{q_0}\, {\ell_1}}{2} \cdot \begin{pmatrix}\frac{2 {m_A} g+{q_0}\, {\ell_1}}{{q_0}\, {\ell_1}}\\ \frac{{\ell_1}}{6}\\ \frac{{\ell_2}+{\ell_1}}{{\ell_1}}\\ \frac{{{\ell}_{2}^{2}}-{{\ell}_{1}^{2}}}{6 {\ell_1}}\\ \frac{{\ell_2}}{{\ell_1}}\\ -\frac{{{\ell}_{2}^{2}}}{6 {\ell_1}}\end{pmatrix}</math>.<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Equilibrium Conditions | {{MyCodeBlock|title=Equilibrium Conditions | ||
|text=Text | |text=Text | ||
| Zeile 67: | Zeile 93: | ||
==tmp== | ==tmp== | ||
<!--------------------------------------------------------------------------------> | Die Bewegung unserer Brücke in durch zwei geometrische Zwangs-Bedingungen behindert: | ||
# durch das Lager in C: | |||
<math>W_C=0 \text{ bzw. } \delta W_C=0</math> sowie | |||
# durch das Seil über die Umlenkrolle in D: | |||
<math>W_A = -\sqrt{3} \; W_B \text{ bzw. } \delta W_A = -\sqrt{3} \; \delta W_B</math>. | |||
Diese Bedingungen arbeiten wir in die virtuellen Arbeiten des Systems ein und erhalten dann mit den verbleibenden gesuchten Größen | |||
<math>\underline{\tilde{Q}} = \left( \begin{array}{c} \Phi_A \\ W_B\\ \Phi_B \\ \Phi_C\end{array} \right)</math> | |||
das Gleichungssystem | |||
<math>\mathit{EI} \begin{pmatrix}-\frac{6}{{\ell_0}} & \frac{{{3}^{\frac{7}{2}}}+27}{2 {{\ell}_{0}^{2}}} & -\frac{3}{{\ell_0}} & 0\\ \frac{{{3}^{\frac{7}{2}}}+27}{2 {{\ell}_{0}^{2}}} & -\frac{{{3}^{\frac{9}{2}}}+486}{{{\ell}_{0}^{3}}} & \frac{{{3}^{\frac{7}{2}}}-81}{2 {{\ell}_{0}^{2}}} & -\frac{54}{{{\ell}_{0}^{2}}}\\ -\frac{3}{{\ell_0}} & \frac{{{3}^{\frac{7}{2}}}-81}{2 {{\ell}_{0}^{2}}} & -\frac{18}{{\ell_0}} & -\frac{6}{{\ell_0}}\\ 0 & -\frac{54}{{{\ell}_{0}^{2}}} & -\frac{6}{{\ell_0}} & -\frac{17}{{\ell_0}}\end{pmatrix} \begin{pmatrix}{{\Phi }_A}\\ {W_B}\\ {{\Phi }_B}\\ {{\Phi }_C}\end{pmatrix} = {m_B}\,g \begin{pmatrix}-\frac{{\ell_0}}{27}\\ -\frac{5 \sqrt{3}-16}{10 \sqrt{3}}\\ \frac{{\ell_0}}{36}\\ \frac{{\ell_0}}{108}\end{pmatrix} | |||
</math>.<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Geometric Constraints | {{MyCodeBlock|title=Geometric Constraints | ||
|text=Text | |text=Text | ||
| Zeile 77: | Zeile 118: | ||
==tmp== | ==tmp== | ||
Das Lösen des Gleichungssystems liefert dann | |||
<math>\displaystyle \left(\begin{array}{c} W_A\\ \Phi_A\\W_B\\\Phi_B\\W_C\\\Phi_C \end{array}\right) = \frac{m_B\, g\, \ell_0^3}{3 \; E I} \left(\begin{array}{l} +0.00291 \\ +0.01169 \frac{1}{\ell_0}\\ -0.00168 \\ -0.00704 \frac{1}{\ell_0}\\ +0\\ +0.006198 \frac{1}{\ell_0} \end{array} \right)</math>. | |||
<!--------------------------------------------------------------------------------> | <!--------------------------------------------------------------------------------> | ||
{{MyCodeBlock|title=Solving | {{MyCodeBlock|title=Solving | ||
|text=Text | |text=Text | ||
| Zeile 87: | Zeile 134: | ||
==tmp== | ==tmp== | ||
<!--------------------------------------------------------------------------------> | Und die Ergebnisse können wir uns anschauen ... | ||
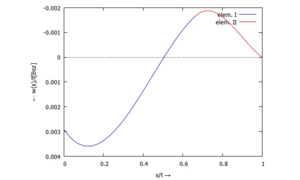
===== ... für ''w(x)'': ===== | |||
[[Datei:Kw52-11.png|mini|Auslenkung ''w(x)''|alternativtext=|ohne]] | |||
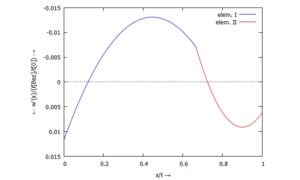
===== ... für ''Φ(x)'': ===== | |||
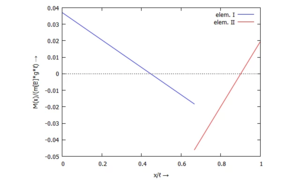
===== ... für ''M(x)'': ===== | |||
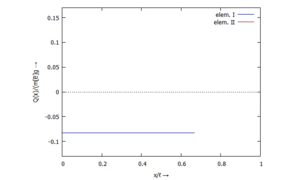
===== ... für ''Q(x)'': =====<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Post-Processing | {{MyCodeBlock|title=Post-Processing | ||
|text=Text | |text=Text | ||
| Zeile 94: | Zeile 155: | ||
1+1 | 1+1 | ||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }}[[Datei:Kw52-12.png|mini|Kippung der Querschnitte ''Φ(x)'']] | ||
[[Datei:Kw52-12.png|mini|Kippung der Querschnitte ''Φ(x)'']] | |||
[[Datei:Kw52-13.png|mini|Moment ''M(x)'']] | [[Datei:Kw52-13.png|mini|Moment ''M(x)'']] | ||
[[Datei:Kw52-14.png|mini|Querkraft ''Q(x)'']] | [[Datei:Kw52-14.png|mini|Querkraft ''Q(x)'']] | ||
Version vom 31. März 2021, 05:56 Uhr
Aufgabenstellung
Eine Brücke ABC der Masse mB und homogener Biegesteifigkeit EI ist in C gelenkig gelagert und in A sowie B mit einem Seil verbunden. Das undehnbare Seil wird dabei über eine kleine Rolle (Radius r ≪ ℓ) in D haftungsfrei geführt. In Punkt C ist die Brücke über eine Drehfeder der Steifigkeit KC mit dem Lager verbunden. In A steht eine Person der Masse mA.
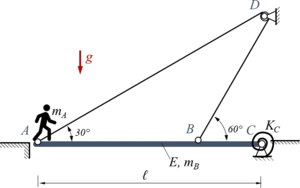
Geben Sie die Lösung für ein Euler-Bernoulli-Modell der Brücke mit dem Ansatz der Finiten Elemente an.
Dies ist eine Näherungslösung zu Kw50. Ermitteln Sie die genäherten Verläufe der Schnittgrößen und Verschiebungen im Balken für diese Parameter:
Lösung mit Maxima
Für die Lösung nutzen wir direkt die Elemente aus der FEM-Formulierung für den Euler-Bernoulli-Balken.
tmp
Header
Text
1+1
tmp
Wir arbeiten mit den selben Parametern und Bezugslängen, wie in Kw50.
Declarations
Text
1+1
tmp
Wir nutzen zwei Finite Elemente für die Brücke und setzen dafür die klassischen Hermite-Polynome, i.e. Polynome dritten Grades, an.
An den drei Knotenpunkten A, B und C haben wir also zusammen die Koordinaten
.
Formfunctions
Text
1+1
tmp
Für die Gleichgewichtsbedingung
konstruieren wir - ohne Berücksichtung der geometrischen Zwangsbedingungen -
mit
und
mit
.
Equilibrium Conditions
Text
1+1
tmp
Die Bewegung unserer Brücke in durch zwei geometrische Zwangs-Bedingungen behindert:
- durch das Lager in C:
sowie
- durch das Seil über die Umlenkrolle in D:
.
Diese Bedingungen arbeiten wir in die virtuellen Arbeiten des Systems ein und erhalten dann mit den verbleibenden gesuchten Größen
das Gleichungssystem
.
Geometric Constraints
Text
1+1
tmp
Das Lösen des Gleichungssystems liefert dann
.
Solving
Text
1+1
tmp
Und die Ergebnisse können wir uns anschauen ...
... für w(x):
... für Φ(x):
... für M(x):
... für Q(x):
Post-Processing
Text
1+1
Links
- Aufgabe Kw50 (analytische Lösung dieser Aufgabe)
- Aufgabe Kw52 (Lösung dieser Aufgabe mit dem Ansatz von Rayleigh-Ritz und Lagrange-Multiplikator)
- Aufgabe Kw53 (Lösung dieser Aufgabe mit dem Ansatz von Rayleigh-Ritz)
Literature
- ...