Gelöste Aufgaben/Kw52

Aufgabenstellung

Eine Brücke ABC der Masse m_B und homogener Biegesteifigkeit EI ist in C gelenkig gelagert und in A sowie B mit einem Seil verbunden. Das undehnbare Seil wird dabei über eine kleine Rolle (Radius r ≪ ℓ) in D haftungsfrei geführt. In Punkt C ist die Brücke über eine Drehfeder der Steifigkeit K_C mit dem Lager verbunden. In A steht eine Person der Masse m_A.

Lageplan (wie Kw50)

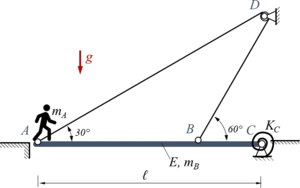
Geben Sie die Lösung für ein Euler-Bernoulli-Modell der Brücke mit dem Verfahren von Rayleigh-Ritz (EBB) an - hier mit Lagrange-Multiplikator für die geometrische Zwangsbedingung.

Dies ist eine Näherungslösung zu Kw50.

Ermitteln Sie die genäherten Verläufe der Schnittgrößen und Verschiebungen im Balken für diese Parameter:

${\begin{array}{ll}K_{C}=&\displaystyle 5{\frac {E\,I}{\ell _{0}}}\\m_{A}=&\displaystyle {\frac {m_{B}}{5}}\end{array}}$

Lösung mit Maxima

In dieser Aufgabe berechnen wir eine Näherungslösung nach dem Verfahren von Rayleigh-Ritz (EBB) zu Kw50.

Alle Überlegungen zur Geometrie des Systems übernehmen wir.

Header

Für die Lösung nutzen wir hier das Ritz-Verfahren mit einer Variante:

• die geometrische Zwangsbedingung für die Punkte A, B durch das Seil erfassen wir durch einen Lagrange-Multiplikator.

/*******************************************************/
/* MAXIMA script                                       */
/* version: wxMaxima 18.10.1                           */
/* author: Andreas Baumgart                            */
/* last updated: 2019-02-12                            */
/* ref: TM-C, Labor 1, dimensionless representation    */
/* description: finds the rayleigh-ritz with Lagragian */
/*              Multiplyers for lab problem #3         */
/*******************************************************/

Declarations

Wir arbeiten mit den selben Parametern und Bezugslängen, wie in Kw50.

Insbesondere gilt auch hier wieder

$\displaystyle W_{B}=-{\frac {W_{A}}{\sqrt {3}}}$.

/* declare variational variables - see 6.3 Identifiers */
declare("Δs", alphabetic);
declare( "ϕ", alphabetic); /* = dw/dx*/
declare( "Π", alphabetic); /* elastic potential */
declare( "ℓ", alphabetic);
declare( "λ", alphabetic);
declare( "Λ", alphabetic);

assume(ℓ[0]>0);

/* system parameters                                  */
params: [K[C]     = kappa*EI/ℓ[0],
         q[0]     = m[B]*g/ℓ[0],
         m[A]     = theta*m[B],
         theta    = 1/5,
         kappa    = 5];

geometry: [alpha[A] = 30*%pi/180,
           alpha[B] = 60*%pi/180,
           ℓ[0]     = ℓ[1]+ℓ[2],
           Δs[A]    = W[A]*sin(alpha[A]),
           Δs[B]    = W[B]*sin(alpha[B]),
           tan(alpha[B]) = H/ℓ[2],
           tan(alpha[A]) = H/ℓ[0],
           xi[1]    = ℓ[1]/ℓ[0],
           xi[2]    = ℓ[2]/ℓ[0]];
geometry: ratsimp(solve(geometry,[alpha[A],alpha[B],ℓ[1],ℓ[2],Δs[A],Δs[B],H,xi[1],xi[2]])[1]);

/* reference length selected:                         */
dimless : ℓ[Bez] = 1/3*m[B]*g*ℓ[0]^3/(EI); /*cantilevered*/

Formfunctions

Nach "Ritz" wählen wir Trial-Functions über die gesamte Stablänge und müssen uns überlegen, welchen Aufwand wir dafür treiben wollen.

Intuitiv wählen wir  für jeden Punkt A, B, C jeweils eine Koordinate, hier

${\begin{array}{l}w(0)=W_{A}\\w(\ell _{1})=W_{B}\\\displaystyle {\frac {dw}{dx}}|_{x=\ell }=\Phi _{C}\end{array}}$.

und brauchen - zusammen der geometrischen Randbedingung w(ℓ)=0 ein Polynom mit vier freien Parametern - also ein Polynom dritten Grades.

Mit dem Ansatz für die Formfunktion

$\displaystyle {\tilde {w}}(x)=\sum _{i=0}^{3}C_{i}\cdot x^{i}$

kommt aus den Bedingungen oben dann

$\displaystyle {\tilde {w}}(\xi )=\sum _{i=1}^{3}Q_{i}\cdot \phi _{i}(\xi )$

mit

${\underline {Q}}=\left({\begin{array}{c}W_{A}\\W_{B}\\\Phi _{C}\end{array}}\right)$.

Trial-Functions

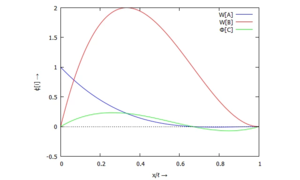
Und so sehen sie aus, unsere drei Trial-Functions:

Für die Formfunktion gilt aber immer die geometrische Zwangsbedingung:

$\displaystyle W_{B}=-{\frac {W_{A}}{\sqrt {3}}}$.

/* coordinates                                        */
Q : [W[A],W[B],Phi[C],λ];
/* raw trial function                                 */
v(x) := sum(C[i]*x^i,i,0,3);

/* formfunctions                                      */
const: [subst([x= 0  ],      v(x)  ) = W[A],
        subst([x=ℓ[1]],      v(x)  ) = W[B],
        subst([x=ℓ[0]], diff(v(x),x))= Phi[C],
        subst([x=ℓ[0]],      v(x)  ) =  0  ];
trials : expand(subst(solve(subst(geometry,const), makelist(C[i],i,0,3))[1],v(x)));
phi : makelist(ratsimp(coeff(trials,Q[i])),i,1,3);

Equilibrium Conditions

Die Potentiale aus Elastischer Energien und Arbeitsfunktion der Gewichtskräfte sind

${\begin{array}{lll}U=&&\displaystyle {\frac {1}{2}}\cdot \int _{0}^{\ell }EI\;w''^{2}\;dx+{\frac {1}{2}}\cdot K_{C}\cdot \Phi _{C}^{2}\\&-&\displaystyle \int _{0}^{\ell }q_{0}\;w\;dx-m_{A}\,g\;W_{A}\end{array}}$.

Nach dem Prinzip vom Minimum der Potentiellen Energie ist das System im Gleichgewicht, wenn das Potential U des Systems

$\displaystyle {\frac {dU}{dQ_{i}}}=0{\text{ für }}Q_{i}\in \left(W_{A},W_{B},\Phi _{C}\right)$

erfüllt. Und sich zusätzlich an die Zwangsbedingung hält!

/******************************************************/
/* Boundary Value Problem Formulation                 */
/* elastic and gravitational potential                */

PMPE : [Π[P] = 1/2*integrate(EI*'diff(w(x),x,2)^2, x,0,ℓ[0]) + 1/2*K[C]*Phi[C]^2,
        A[P] =  integrate(q[0]*w(x), x,0,ℓ[0]) + m[A]*g*W[A]];

Geometric Constraints

Das können wir mit dem Konzept der Lagrange-Multiplikatoren erfassen. Dafür schreiben wir

$\Lambda ({\underline {Q}})=U+\lambda \cdot \underbrace {\left(\Delta s_{A}+\Delta s_{B}\right)} _{\displaystyle \equiv {\sqrt {3}}\,W_{B}+W_{A}}$

mit dem Lagrange-Multiplikator λ. Die neuen Gleichgewichtsbedingungen lauten nun

$\displaystyle {\frac {d\Lambda }{dQ_{i}}}=0{\text{ für alle }}Q_{i}$

und wir erhalten die vier Gleichungen

${\begin{array}{cc}\displaystyle {\frac {\lambda }{2}}-{\frac {49{m_{B}}g}{120}}-{\frac {17{{\Phi }_{C}}\,EI}{\ell _{0}^{2}}}-{\frac {108{W_{B}}\,EI}{\ell _{0}^{3}}}+{\frac {19{W_{A}}\,EI}{\ell _{0}^{3}}}&=0\\\displaystyle {\frac {{\sqrt {3}}\lambda }{2}}-{\frac {9{m_{B}}g}{8}}+{\frac {135{{\Phi }_{C}}\,EI}{\ell _{0}^{2}}}+{\frac {729{W_{B}}\,EI}{\ell _{0}^{3}}}-{\frac {108{W_{A}}\,EI}{\ell _{0}^{3}}}&=0\\\displaystyle -{\frac {{\ell _{0}}\,{m_{B}}g}{12}}+{\frac {33{{\Phi }_{C}}\,EI}{\ell _{0}}}+{\frac {135{W_{B}}\,EI}{\ell _{0}^{2}}}-{\frac {17{W_{A}}\,EI}{\ell _{0}^{2}}}&=0\\\displaystyle {\frac {{\sqrt {3}}\,{W_{B}}}{2}}+{\frac {W_{A}}{2}}&=0\end{array}}$.

/* gemetric constraints                               */
trials: w(x) = sum(Q[i]*phi[i],i,1,3);
print('phi = expand(subst([x=ℓ[0]*xi],phi)))$

plot2d(ratsimp(subst([x = xi*ℓ[0]],phi)*[1,1,1/ℓ[0]]), [xi,0,1],
            [legend, "W[A]","W[B]","Φ[C]"], [xlabel, "x/ℓ →"], [ylabel, "ϕ[i] →"]);

PMPE: subst(trials, PMPE);
PMPE: ev(PMPE,nouns);

U: expand(subst(PMPE,Π[P] - A[P]));

/* Lagrange-Function                                  */
Λ : U + subst(geometry,λ*(Δs[A]+Δs[B]));

/* Equilibrium Conditions                             */
eom : subst(params,makelist( diff(Λ,Q[i])=0, i,1,4));

Solving

Das Lösen des Gleichungssystems liefert dann

$\displaystyle \left({\begin{array}{c}W_{A}\\W_{B}\\\Phi _{C}\\\lambda \end{array}}\right)={\frac {m_{B}\,g\,\ell _{0}^{3}}{3\;EI}}\left({\begin{array}{l}-3.7810^{-5}\\+2.1810^{-5}\\\displaystyle +0.00747{\frac {1}{\ell _{0}}}\\\displaystyle +2.71{\frac {EI}{\ell _{0}^{3}}}\end{array}}\right)$.

/* Solving                                            */
sol: float(solve(eom,Q)[1]);

Post-Processing

Und die Ergebnisse können wir uns anschauen ...

... für w(x):

Auslenkung w(x)

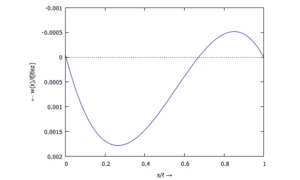
... für Φ(x):

Kippwinkel Φ(x)

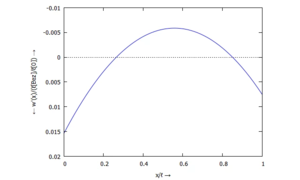
... für M(x):

Biegemoment M(x)

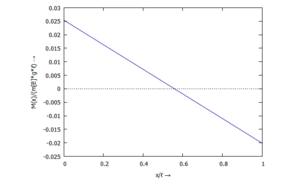
... für Q(x):

Querkraft Q(x)

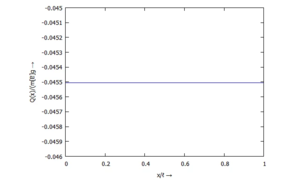
/* Post-Processing                                    */
w : subst([x=xi*ℓ[0]],subst(geometry,subst(sol, sum(Q[j]*phi[j],j,1,3))));

fcts: [         w             ,
           diff(w,xi  )/ℓ[0]  ,
       -EI*diff(w,xi,2)/ℓ[0]^2,
       -EI*diff(w,xi,3)/ℓ[0]^3];
fcts: float(subst(geometry,expand(fcts)))$ 
facts: [1/ℓ[Bez], ℓ[0]/ℓ[Bez], 1/(m[B]*g*ℓ[0]), 1/(m[B]*g)];
 
textlabels : ["← w(x)/ℓ[Bez]", "← w'(x)/(ℓ[Bez]/ℓ[0]) →", "M(x)/(m[B]*g*ℓ) →", "Q(x)/(m[B]g →"];
for i: 1 thru 4 do(
  f : expand(subst(dimless,facts[i]*fcts[i])),
  preamble: if i<=2 then "set yrange [] reverse" else "set yrange []",
  plot2d(f, [xi,0,1], [legend, false],
                      [gnuplot_preamble, preamble],
                      [xlabel, "x/ℓ →"],
                      [ylabel, textlabels[i]]))$

---

Links

• Aufgabe Kw50 (analytische Lösung dieser Aufgabe)
• Aufgabe Kw52 (Lösung dieser Aufgabe mit dem Ansatz von Rayleigh-Ritz und Lagrange-Multiplikator)
• Aufgabe Kw53 (Lösung dieser Aufgabe mit dem Ansatz von Rayleigh-Ritz)

Literature

• ...