Gelöste Aufgaben/Kw29: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 6: | Zeile 6: | ||
==Aufgabenstellung== | ==Aufgabenstellung== | ||
In einer Sporthalle wird ein Federball (Punktmasse ''m'') mit einer Anfangsgeschwindigkeit ''v<sub>0</sub>'' unter einem Winkel ''α'' gegenüber der Horizontalen abgeschlagen. Der Strömungswiderstand des Federballs wird mit | |||
<onlyinclude> | <math>W = \gamma\cdot v^2</math> | ||
[[Datei: | |||
angegeben, dabei ist ''γ'' eine gemessene Größe.<onlyinclude> | |||
[[Datei:Kw29-02.png|alternativtext=|links|mini|200x200px|Lageplan]] | |||
Schreiben Sie die Bewegungsgleichung des Federballs an. Formulieren Sie die Bewegungsgleichung des Federballs in dimensionsloser Form und berechnen Sie die Lösung numerisch als Anfangswertproblem. | |||
</onlyinclude> | </onlyinclude> | ||
Gegeben: ''g, m, γ, v<sub>0</sub>'' | |||
== Lösung mit Maxima == | == Lösung mit Maxima == | ||
==tmp== | |||
[[Datei:Kw29-02.png|mini|Lageplan|alternativtext=|200x200px]]Die Koordinaten der Bewegung des Federballs sind | |||
* u(t) in horizontale und | |||
* w(t) in vertikale Richtung. | |||
Als Parameter der Bewegung wählen wir: | |||
<math>\begin{array}{lll}h_0&=2\;\text{m} &\ldots\text{ Anfangshöhe}\\v_0&=65\;\text{km/h} &\ldots\text{ Anfangsgeschwindigkeit}\\\end{array}</math>.<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Header | {{MyCodeBlock|title=Header | ||
|text=Text | |text=Text | ||
| Zeile 27: | Zeile 36: | ||
==tmp== | ==tmp== | ||
<!--------------------------------------------------------------------------------> | Die Bewegungsgleichungen in horizontale und vertikale Richtung sind | ||
<math>\begin{array}{ll}m\;\ddot{u} + W\cdot \cos(\alpha) &= 0\\m\;\ddot{w} + W\cdot \sin(\alpha) &= -m\,g\end{array}</math>. | |||
Dabei ist | |||
<math>\begin{array}{rl}v &= \sqrt{\dot{u}^2+\dot{w}^2}\\\cos\alpha&=\displaystyle \frac{\dot{u}}{v}\\\sin\alpha&=\displaystyle \frac{\dot{w}}{v}\end{array}</math>. | |||
Als nächstes machen wir die Bewegungsgleichungen dimensionslos mit | |||
* der dimensionslosen Zeit <math>\displaystyle \tau = \frac{t}{T}</math> und | |||
* den dimensionslosen Koordinaten <math>\displaystyle U = \frac{u}{L} \text{ bzw. } W = \frac{w}{L}</math>, | |||
dabei sind ''T = h<sub>0</sub> / v<sub>0</sub>'' die Bezugszeit und ''L ''= h<sub>0</sub>'''' die Bezugslänge. | |||
Die neuen Form der nichtlinearen Bewegungsgleichung ergibt sich dann zu | |||
<math>\begin{array}{ll} \frac{{{d}^{2}}}{d{{\tau}^{2}}}\cdot U&=-\Gamma\cdot \left( \frac{d}{d\tau}\cdot U\right) \cdot \sqrt{{{\left( \frac{d}{d\tau}\cdot W\right) }^{2}}+{{\left( \frac{d}{d\tau}\cdot U\right) }^{2}}},\\ \frac{{{d}^{2}}}{d\,{{\tau}^{2}}}\cdot W&=-\Gamma\cdot \left( \frac{d}{d\tau}\cdot W\right) \cdot \sqrt{{{\left( \frac{d}{d\tau}\cdot W\right) }^{2}}+{{\left( \frac{d}{d\tau}\cdot U\right) }^{2}}}-G \end{array}</math>, | |||
die wir numerisch lösen.<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Equilibrium Conditions | {{MyCodeBlock|title=Equilibrium Conditions | ||
|text=Text | |text=Text | ||
| Zeile 37: | Zeile 66: | ||
==tmp== | ==tmp== | ||
<!--------------------------------------------------------------------------------> | Für ''Γ''=1/2 und ''α<sub>0</sub>'' = 30° lösen wir das Problem numerisch, dazu wählen wir als Anfangsbedingungen | ||
<math>\begin{array}{ll}U(0)&=0\\W(0)&=1\\\frac{d}{d\tau}\left. U\right|_{\tau=0}&=\cos\alpha_0\\\frac{d}{d\tau}\left. W\right|_{\tau=0}&=\sin\alpha_0\end{array}</math>.<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Solving | {{MyCodeBlock|title=Solving | ||
|text=Text | |text=Text | ||
| Zeile 47: | Zeile 79: | ||
==tmp== | ==tmp== | ||
Die Flugbahn des Federballs erhalten durch den Parameter-Plot mit ''W(τ)'' über ''U(τ)''.[[Datei:Kw29-11.png|mini|Flugbahn|alternativtext=|ohne]] | |||
<!--------------------------------------------------------------------------------> | <!--------------------------------------------------------------------------------> | ||
{{MyCodeBlock|title=Post-Processing | {{MyCodeBlock|title=Post-Processing | ||
| Zeile 60: | Zeile 93: | ||
<tr><td></td><td></td></tr> | <tr><td></td><td></td></tr> | ||
</table> | </table> | ||
<hr/> | <hr/> | ||
Version vom 29. März 2021, 11:19 Uhr
Aufgabenstellung
In einer Sporthalle wird ein Federball (Punktmasse m) mit einer Anfangsgeschwindigkeit v0 unter einem Winkel α gegenüber der Horizontalen abgeschlagen. Der Strömungswiderstand des Federballs wird mit
angegeben, dabei ist γ eine gemessene Größe.
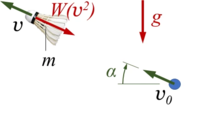
Schreiben Sie die Bewegungsgleichung des Federballs an. Formulieren Sie die Bewegungsgleichung des Federballs in dimensionsloser Form und berechnen Sie die Lösung numerisch als Anfangswertproblem.
Gegeben: g, m, γ, v0
Lösung mit Maxima
tmp

Die Koordinaten der Bewegung des Federballs sind
- u(t) in horizontale und
- w(t) in vertikale Richtung.
Als Parameter der Bewegung wählen wir:
.
Header
Text
1+1
tmp
Die Bewegungsgleichungen in horizontale und vertikale Richtung sind
.
Dabei ist
.
Als nächstes machen wir die Bewegungsgleichungen dimensionslos mit
- der dimensionslosen Zeit und
- den dimensionslosen Koordinaten ,
dabei sind T = h0 / v0 die Bezugszeit und L = h0' die Bezugslänge.
Die neuen Form der nichtlinearen Bewegungsgleichung ergibt sich dann zu
,
die wir numerisch lösen.
Equilibrium Conditions
Text
1+1
tmp
Für Γ=1/2 und α0 = 30° lösen wir das Problem numerisch, dazu wählen wir als Anfangsbedingungen
.
Solving
Text
1+1
tmp
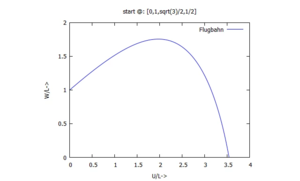
Die Flugbahn des Federballs erhalten durch den Parameter-Plot mit W(τ) über U(τ).
Post-Processing
Text
1+1
Links
- ...
Literature
- ...