Gelöste Aufgaben/Kw25: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 13: | Zeile 13: | ||
==Aufgabenstellung== | ==Aufgabenstellung== | ||
Ein Körper (Masse ''m'') liegt auf einem Band, das über eine Rolle (Radius ''r'') mit konstanter Drehgeschwindigkeit Ω angetrieben wird. Der Körper ist über eine Feder (Steifigkeit ''k'') mit der Umgebung verbunden. Zwischen Körper und Band wirkt trockene Reibung (''μ, μ<sub>0</sub>''). | |||
<onlyinclude> | <onlyinclude> | ||
[[Datei: | [[Datei:Kw25-01.png|alternativtext=|links|mini|Lageplan]] | ||
Gesucht ist | Gesucht ist die numerische Lösung für den Klotz auf dem Band als Anfangswertproblem, untersucht werden selbsterregte Schwingungen. | ||
</onlyinclude> | </onlyinclude> | ||
| Zeile 25: | Zeile 25: | ||
==tmp== | ==tmp== | ||
<!--------------------------------------------------------------------------------> | "Stick-Slip" Schwingungen sind klassische selbsterregte Schwingungen. Selbsterrung heißt: das System lenkt den Energiefluss im System so, dass Schwingungen "aus sich heraus" angeregt werden. Charakteristisch für "Stick-Slip" Schwingungen ist, dass zwei Körper zeitweise aneinander haften, dann auseinander gerissen werden und dann aneinander reiben - bis sie wieder aneinander haften.<!--------------------------------------------------------------------------------> | ||
{{MyCodeBlock|title=Title | {{MyCodeBlock|title=Title | ||
|text=Text | |text=Text | ||
| Zeile 36: | Zeile 37: | ||
==tmp== | ==tmp== | ||
<!--------------------------------------------------------------------------------> | Im Zentrum dieser Aufgabe steht die Kennlinie (engl.: Characteristic), die den Zusammenhang zwischen Tangentialkräft (Haftkraft, Reibkraft), Normalkraft und Relativgeschwindigkeit erfasst. | ||
Dafür brauchen wir hier drei Parameter. | |||
* ''a=μ / μ<sub>0;</sub>'' | |||
* ''b'' : erfasst, welchen Ausschnitt der Sinus-Funktion wir nutzen; | |||
* ''v<sub>0</sub>'': eine (kleine) Kriechgeschwindigkeit.<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Title | {{MyCodeBlock|title=Title | ||
|text=Text | |text=Text | ||
| Zeile 47: | Zeile 55: | ||
==tmp== | ==tmp== | ||
<!--------------------------------------------------------------------------------> | Trockene Reibung im Modell beschreibt man mit zwei System-Parametern: | ||
* dem Reibungskoeffizient ''μ'' und | |||
* dem Haftungskoeffizient ''μ<sub>0</sub>''. | |||
Haften Körper und Unterlage aneinander (Relativgeschwindigkeit ''v<sub>r</sub>'' ist "Null"), so ist die Haftkraft | |||
mit der Normalkraft ''N''. Bewegen sich die beiden relativ zueinander, so schreibt man | |||
. | |||
Die Beträge bedeuten hier: die Kräfte sind gegen die Bewegung orientiert. | |||
Für die numerische Lösung des Anfangswertproblems ist diese Bescheibung eine Katastrophe! | |||
# Wir haben eine Kennlinie mit Sprung zwischen ''μ'' und ''μ<sub>0</sub>''. | |||
# Das Vorzeichen des Funktionswerts für Haftung hängt davon ab, mit welcher Orientierung eine resultierende Kraft auf den Körper wirkt. | |||
Der Sprung ist eine effektive Handbremse für jeden Algorithmus zur numerischen Integration der Bewegungsgleichung, der von einer stetigen und stetig differenzierbaren "Rechten Seite" der Bewegungsgleichung ausgehen (vgl. Runge-Kutta-Verfahren 4.ter Ordnung) - also für praktisch alle Algorithmen. Und dass die Haftkraft nicht eindeutig von den Zustandsgrößen des Systems abhängt, hebelt jedes Standard-Lösungsverfahren aus. | |||
Kommerzielle Programme führen deshalb "Schaltstellen" ein, in denen der Lösungsalgorithmus an diesen Unstetigkeiten dann "etwas anderes" macht. Oft wird die Lösung des Anfangswertproblems dadurch aber sehr ineffizient. Hier schreiben wir deshalb eine Kennlinie an, bei der die Tangentialkraft (hier nennen wir sie Reibkraft) stetig von der Relativgeschwindigkeit ''v<sub>r</sub>'' zwischen Körper und Band abhängt.[[Datei:Kw25-03.png|mini|Reibkennlinie]]Wir suchen eine Kennlinie wie hier im Bild blau und rot gekennzeichnet. Die klassische Formulierung ist in grau hinterlegt. Die Kennlinie unserer Formulierung nennen wir Reibkennlinie | |||
. | |||
Das Haften ist hier nur ein Sonderfall, den die Kennlinine mit abbildet. | |||
Die gesuchte Kennlinie | |||
muss punkt-symmetrisch sein (die Reibkraft ändert ihr Vorzeichen mit der Orientierung der Relativgeschwindigkeit). Welche Funktionen wir verwenden ist egal, hier probieren wir Sinus und Exponential-Funktionen aus. Wie diese Funktioen aneinader-gestückelt werden, steht im Lexikon unter "Reibkennlinie". | |||
Wir arbeiten mit | |||
.<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Title | {{MyCodeBlock|title=Title | ||
|text=Text | |text=Text | ||
| Zeile 104: | Zeile 146: | ||
}} | }} | ||
[[Datei:Kw25-01.png|mini|Lageplan]] | [[Datei:Kw25-01.png|mini|Lageplan]] | ||
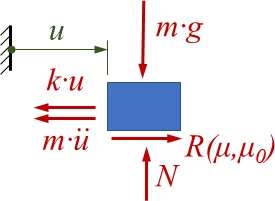
[[Datei:Kw25-02.png|mini|Freikörperbild]] | [[Datei:Kw25-02.png|mini|Freikörperbild]] | ||
Version vom 29. März 2021, 06:46 Uhr
Aufgabenstellung
Ein Körper (Masse m) liegt auf einem Band, das über eine Rolle (Radius r) mit konstanter Drehgeschwindigkeit Ω angetrieben wird. Der Körper ist über eine Feder (Steifigkeit k) mit der Umgebung verbunden. Zwischen Körper und Band wirkt trockene Reibung (μ, μ0).
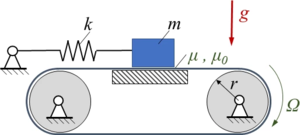
Gesucht ist die numerische Lösung für den Klotz auf dem Band als Anfangswertproblem, untersucht werden selbsterregte Schwingungen.
Lösung mit Maxima
Lorem Ipsum ....
tmp
"Stick-Slip" Schwingungen sind klassische selbsterregte Schwingungen. Selbsterrung heißt: das System lenkt den Energiefluss im System so, dass Schwingungen "aus sich heraus" angeregt werden. Charakteristisch für "Stick-Slip" Schwingungen ist, dass zwei Körper zeitweise aneinander haften, dann auseinander gerissen werden und dann aneinander reiben - bis sie wieder aneinander haften.
Title
Text
1+1
tmp
Im Zentrum dieser Aufgabe steht die Kennlinie (engl.: Characteristic), die den Zusammenhang zwischen Tangentialkräft (Haftkraft, Reibkraft), Normalkraft und Relativgeschwindigkeit erfasst.
Dafür brauchen wir hier drei Parameter.
- a=μ / μ0;
- b : erfasst, welchen Ausschnitt der Sinus-Funktion wir nutzen;
- v0: eine (kleine) Kriechgeschwindigkeit.
Title
Text
1+1
tmp
Trockene Reibung im Modell beschreibt man mit zwei System-Parametern:
- dem Reibungskoeffizient μ und
- dem Haftungskoeffizient μ0.
Haften Körper und Unterlage aneinander (Relativgeschwindigkeit vr ist "Null"), so ist die Haftkraft
mit der Normalkraft N. Bewegen sich die beiden relativ zueinander, so schreibt man
.
Die Beträge bedeuten hier: die Kräfte sind gegen die Bewegung orientiert.
Für die numerische Lösung des Anfangswertproblems ist diese Bescheibung eine Katastrophe!
- Wir haben eine Kennlinie mit Sprung zwischen μ und μ0.
- Das Vorzeichen des Funktionswerts für Haftung hängt davon ab, mit welcher Orientierung eine resultierende Kraft auf den Körper wirkt.
Der Sprung ist eine effektive Handbremse für jeden Algorithmus zur numerischen Integration der Bewegungsgleichung, der von einer stetigen und stetig differenzierbaren "Rechten Seite" der Bewegungsgleichung ausgehen (vgl. Runge-Kutta-Verfahren 4.ter Ordnung) - also für praktisch alle Algorithmen. Und dass die Haftkraft nicht eindeutig von den Zustandsgrößen des Systems abhängt, hebelt jedes Standard-Lösungsverfahren aus.
Kommerzielle Programme führen deshalb "Schaltstellen" ein, in denen der Lösungsalgorithmus an diesen Unstetigkeiten dann "etwas anderes" macht. Oft wird die Lösung des Anfangswertproblems dadurch aber sehr ineffizient. Hier schreiben wir deshalb eine Kennlinie an, bei der die Tangentialkraft (hier nennen wir sie Reibkraft) stetig von der Relativgeschwindigkeit vr zwischen Körper und Band abhängt.
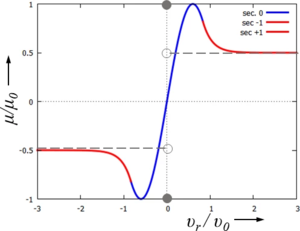
Wir suchen eine Kennlinie wie hier im Bild blau und rot gekennzeichnet. Die klassische Formulierung ist in grau hinterlegt. Die Kennlinie unserer Formulierung nennen wir Reibkennlinie
.
Das Haften ist hier nur ein Sonderfall, den die Kennlinine mit abbildet.
Die gesuchte Kennlinie
muss punkt-symmetrisch sein (die Reibkraft ändert ihr Vorzeichen mit der Orientierung der Relativgeschwindigkeit). Welche Funktionen wir verwenden ist egal, hier probieren wir Sinus und Exponential-Funktionen aus. Wie diese Funktioen aneinader-gestückelt werden, steht im Lexikon unter "Reibkennlinie".
Wir arbeiten mit
.
Title
Text
1+1
tmp
Title
Text
1+1
tmp
Title
Text
1+1
tmp
a)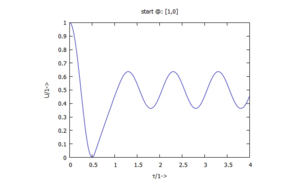
| b)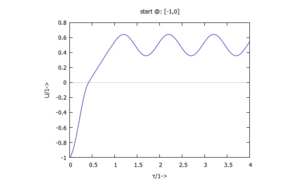
|
c)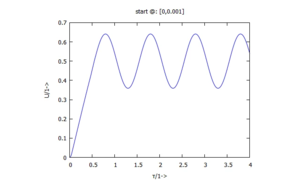 | d)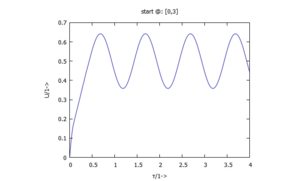 |
a)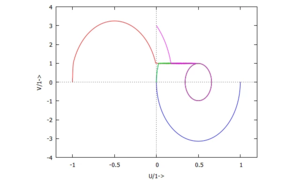 |
b)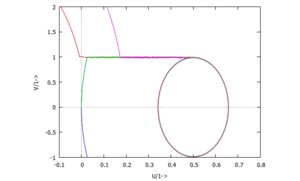 |
Post-Processing
Text
1+1

Links
- ...
Literature
- ...