Gelöste Aufgaben/Kit6: Unterschied zwischen den Versionen
Zur Navigation springen
Zur Suche springen
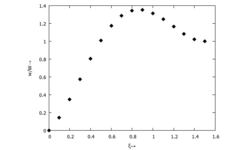
Samples von ''w(x)''. 
Caption
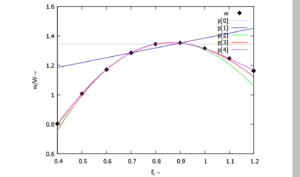
Polynom-Approximation (Detail) 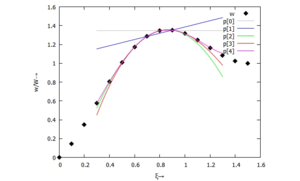
w(x) 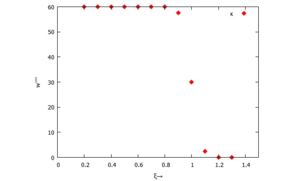
Vierte Ableitung w''''
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 8: | Zeile 8: | ||
Von einen Funktionsverlauf (hier aus [[Gelöste Aufgaben/Kit5|Kit5]]) wurden die skizzierten Samples ermittelt, aus denen bzgl. eines Referenzpunktes die Ableitungen bis zur vierten Ordnung ermittelt werden sollen. | Von einen Funktionsverlauf (hier aus [[Gelöste Aufgaben/Kit5|Kit5]]) wurden die skizzierten Samples ermittelt, aus denen bzgl. eines Referenzpunktes die Ableitungen bis zur vierten Ordnung ermittelt werden sollen. | ||
<onlyinclude> | <onlyinclude> | ||
[[Datei:Kit6-01.png|left|248px|mini|Samples von <nowiki>''w(x)''</nowiki>.]] | |||
[[Datei:Screenshot 20210111-063733~2.png|100px|left|mini|Caption]] | [[Datei:Screenshot 20210111-063733~2.png|100px|left|mini|Caption]] | ||
Gesucht ist eine numerische Approximation der Ableitungen bis zur vierten Ordnung aus Samples der Lösung eines [[Randwertprobleme/Methoden zur Lösung von Randwertproblemen/Finite Differenzen Verfahren (EBB)|Randwertproblems]]. | Gesucht ist eine numerische Approximation der Ableitungen bis zur vierten Ordnung aus Samples der Lösung eines [[Randwertprobleme/Methoden zur Lösung von Randwertproblemen/Finite Differenzen Verfahren (EBB)|Randwertproblems]]. | ||
Hier wird der Bezug zur Methode der Finiten Differenzen gezeigt. | |||
</onlyinclude> | </onlyinclude> | ||
== Lösung mit Maxima == | == Lösung mit Maxima == | ||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Header | |||
|text= | |||
Der Funktionsverlauf für dieses Beispiel kommt aus Aufgabe [[Gelöste Aufgaben/Kit4|Kit4]]. | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
1+1 | |||
</syntaxhighlight> | |||
}} | |||
==tmp== | ==tmp== | ||
Stützstellen (Samples) eines Funktionsverlaufs erhalten wir, wenn wir die Funktion | |||
::<math>w(\xi)= \left\{ \begin{array}{ll} \displaystyle \frac{5\cdot {{\xi}^{4}}}{2}-\frac{194\cdot {{\xi}^{3}}}{27}+5\cdot {{\xi}^{2}}+\xi & \text{ für } 0\le \xi \le 1 \\ \displaystyle \frac{19\cdot {{\xi}^{3}}}{54}-\frac{7\cdot {{\xi}^{2}}}{18}-\frac{5\cdot \xi}{18}+\frac{71}{54} & \text{ für } 1 < \xi \le 3/2 \end{array} \right.</math> | |||
in regelmäßigen Intervallen abtasten. | |||
Das Bild oben zeigt die N= 16 Samples zu dieser Funktion. | |||
<!--------------------------------------------------------------------------------> | <!--------------------------------------------------------------------------------> | ||
{{MyCodeBlock|title= | {{MyCodeBlock|title=Preparations | ||
|text=Text | |text=Text | ||
|code= | |code= | ||
| Zeile 24: | Zeile 45: | ||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
==tmp== | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Generic Approximation Polynoms | |||
|text=Text | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
1+1 | |||
</syntaxhighlight> | |||
}} | |||
==tmp== | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Approximation Polynoms for ξ=8∙Δξ | |||
|text=Text | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
1+1 | |||
</syntaxhighlight> | |||
}} | |||
==tmp== | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Check for fourth order derivative | |||
|text=Text | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
1+1 | |||
</syntaxhighlight> | |||
}} | |||
<table class="wikitable"> | <table class="wikitable"> | ||
| Zeile 32: | Zeile 83: | ||
[[Datei:Kig6-12.png|mini|w(x)]] | [[Datei:Kig6-12.png|mini|w(x)]] | ||
[[Datei:Kig6-14.png|mini|Vierte Ableitung w<nowiki>''''</nowiki>]] | [[Datei:Kig6-14.png|mini|Vierte Ableitung w<nowiki>''''</nowiki>]] | ||
Version vom 26. März 2021, 07:22 Uhr
Aufgabenstellung
Von einen Funktionsverlauf (hier aus Kit5) wurden die skizzierten Samples ermittelt, aus denen bzgl. eines Referenzpunktes die Ableitungen bis zur vierten Ordnung ermittelt werden sollen.


Gesucht ist eine numerische Approximation der Ableitungen bis zur vierten Ordnung aus Samples der Lösung eines Randwertproblems.
Hier wird der Bezug zur Methode der Finiten Differenzen gezeigt.
Lösung mit Maxima
Header
Der Funktionsverlauf für dieses Beispiel kommt aus Aufgabe Kit4.
1+1
tmp
Stützstellen (Samples) eines Funktionsverlaufs erhalten wir, wenn wir die Funktion
in regelmäßigen Intervallen abtasten.
Das Bild oben zeigt die N= 16 Samples zu dieser Funktion.
Preparations
Text
1+1
tmp
Generic Approximation Polynoms
Text
1+1
tmp
Approximation Polynoms for ξ=8∙Δξ
Text
1+1
tmp
Check for fourth order derivative
Text
1+1



Links
- ...
Literature
- ...