Gelöste Aufgaben/Kit5: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 11: | Zeile 11: | ||
==Aufgabenstellung== | ==Aufgabenstellung== | ||
Bei diesem Randwertproblem wird ein [[Sources/Lexikon/Euler-Bernoulli-Balken|Euler-Bernoulli-Balken]] (Elastizitätsmodul ''E'', Flächenmoment 2-ten Grades ''I'') mit einer Streckenlast ''q<sub>0</sub>'' im Bereich ''A-B'' belastet. In ''A'' ist der Balken fest eingespannt, wobei durch eine Einbau-Ungenauigkeit der Rand im Verhältnis 1:10 geneigt ist. | |||
<onlyinclude> | In ''B'' hält das verschiebliche Lager den Balken horizontal. Gegen über Punkt A hält das Lager in B den Balken in einem vertikalen Abstand von W zur Horizontalen. | ||
[[Datei:Screenshot 20210111-063733~2.png|100px|left|mini|Caption]] | |||
Gesucht ist | <onlyinclude>[[Datei:Screenshot 20210111-063733~2.png|100px|left|mini|Caption]] | ||
Gesucht ist die Biegelinie des Balkens, der durch geometrische Randbedingungen vorverformt ist. | |||
</onlyinclude> | </onlyinclude> | ||
== Lösung mit Maxima == | == Lösung mit Maxima == | ||
In [[Gelöste Aufgaben/Kit4|Kit4]] finden Sie die Transformation der Bewegungsgleichung des Euler-Bernoulli-Balkens in die dimensionslose Form mit der allgemeinen Lösung | |||
<math>\displaystyle {\tilde{w}_{i}}\left( \xi\right) :=\frac{\mu\cdot {{\xi}^{4}}}{24}+\frac{{{C}_{i,3}}\cdot {{\xi}^{3}}}{6}+\frac{{{C}_{i,2}}\cdot {{\xi}^{2}}}{2}+{{C}_{i,1}}\cdot \xi+{{C}_{i,0}}</math> | |||
für die Bereiche i=1 (''A-B'') und i=2 (''B-C''). | |||
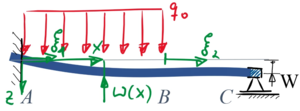
Dazu gehören die neuen dimensionslose Koordinaten ''ξ<sub>1</sub>'' und ''ξ<sub>2</sub>'': | |||
Die Rand- und Übergangsbedingungen lauten dann mit ''ℓ<sub>2</sub> = ℓ<sub>1</sub>/2'' | |||
<math>\begin{array}{ccl} \tilde{w}_1(0)&=&0\\\tilde{w}'_1(0)&=&1/10\end{array}</math>, <math>\begin{array}{ccl} \tilde{w}_1(1)&=&\tilde{w}_2(0)\\\tilde{w}'_1(1)&=&\tilde{w}'_2(0)\\\tilde{w}''_1(1)&=&\tilde{w}''_2(0)\\\tilde{w}'''_1(1)&=&\tilde{w}'''_2(0)\end{array}</math>, <math>\begin{array}{ccl} \tilde{w}_1(1/2)&=&W\\ \tilde{w}'_2(1/2)&=&0\end{array}</math> | |||
==tmp== | ==tmp== | ||
| Zeile 35: | Zeile 46: | ||
<tr><td></td><td></td></tr> | <tr><td></td><td></td></tr> | ||
</table> | </table> | ||
[[Datei:Kit5-11.png|mini|Koordinaten]] | |||
[[Datei:Kit5.png|mini|Lageplan]] | |||
[[Datei:Kit5-12.png|mini|w(x)]] | |||
Version vom 26. März 2021, 06:55 Uhr
Aufgabenstellung
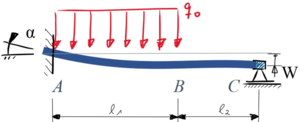
Bei diesem Randwertproblem wird ein Euler-Bernoulli-Balken (Elastizitätsmodul E, Flächenmoment 2-ten Grades I) mit einer Streckenlast q0 im Bereich A-B belastet. In A ist der Balken fest eingespannt, wobei durch eine Einbau-Ungenauigkeit der Rand im Verhältnis 1:10 geneigt ist.
In B hält das verschiebliche Lager den Balken horizontal. Gegen über Punkt A hält das Lager in B den Balken in einem vertikalen Abstand von W zur Horizontalen.
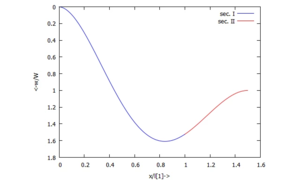
Gesucht ist die Biegelinie des Balkens, der durch geometrische Randbedingungen vorverformt ist.
Lösung mit Maxima
In Kit4 finden Sie die Transformation der Bewegungsgleichung des Euler-Bernoulli-Balkens in die dimensionslose Form mit der allgemeinen Lösung
für die Bereiche i=1 (A-B) und i=2 (B-C).
Dazu gehören die neuen dimensionslose Koordinaten ξ1 und ξ2:
Die Rand- und Übergangsbedingungen lauten dann mit ℓ2 = ℓ1/2
, ,
tmp
Title
Text
1+1
Links
- ...
Literature
- ...