Gelöste Aufgaben/Kit4

Aufgabenstellung

Lageplan

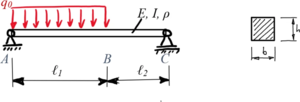
Gesucht ist für den Euler-Bernoulli-Balken die dimensionslose Form der Bewegungs-Differentialgleichung.

Die dimensionsbehaftete Form der Bewegungsgleichung lautet

$E\cdot I\frac{d^4}{d{x}^4}w(x)=q,\text{ mit }\{\begin{array}{l}q=q_0\text{ für }0\le x<{\ell }_1\\ q=0\text{ sonst }\end{array}$

Um die dimensionslose Form der Bewegungsgleichung zu bekommen, ersetzten wir

$E=\tilde{E}\cdot \frac{F_{Bez}}{{\ell }_{Bez}^2};I=\tilde{I}\cdot {\ell }_{Bez}^4;q_0={\tilde{q}}_0\cdot \frac{F_{Bez}}{{\ell }_{Bez}}$.

Dimensionsbehaftet ist jetzt noch w(x) und seine Ableitungen. Mit der Koordinaten-Transformation

$w=\tilde{w}\cdot {\ell }_{Bez}\text{ und }x=\tilde{x}\cdot {\ell }_1$

erhalten wir

$\frac{d^4}{d{x}^4}w(x)={\ell }_{Bez}\cdot \frac{d^4}{d{\tilde{x}}^4}(\tilde{w}(\tilde{x}))\cdot \underset{=\frac{1}{{\ell }_1^4}}{\underbrace{{\left(\frac{d\tilde{x}}{dx}\right)}^4}}$.

Einsetzen liefert

$\tilde{E}\frac{F_{Bez}}{{\ell }_{Bez}^2}\cdot \tilde{I}{\ell }_{Bez}^4\cdot {\ell }_{Bez}\frac{d^4}{d{\tilde{x}}^4}\tilde{w}(\tilde{x})\frac{1}{{\ell }_1^4}=\tilde{q}\frac{F_{Bez}}{{\ell }_{Bez}}$

Die Bezugsgrößen dürfen wir frei wählen - aber wie? Für ℓ_Bez = h drücken wir die Auslenkung w als Vielfaches von h aus - das ist praktisch! Denn damit die Annahmen zur Linearisierung beim Euler-Bernoulli-Balken eingehalten werden, sollte w ≤ h, also

$\tilde{w}\le 1$

Für die Bezugskaft bietet sich F_Bez = G an, wobei G die Gewichtskraft des Balkens ist. Dann ist $\tilde{q}$ das Vielfache der Gewichts-Streckenlast.

Umschreiben und Auflösen liefert mit I = h⁴/12

$\frac{d^4\tilde{w}}{d{\tilde{x}}^4}=\frac{12\cdot {\tilde{q}}_0}{\tilde{E}}{\left(\frac{{\ell }_1}{h}\right)}^4$

oder abgekürzt:

$\frac{d^4\tilde{w}}{d{\tilde{x}}^4}=\mu$

Die dimensionslose Ortskoordinate brauchen wir für den Rest der Aufgaben - man wählt deshalb oft

$\xi :=\tilde{x}\text{ und }\frac{d}{d\xi }(.)=:(.{)}^{\prime }$

und erhält als neue Bewegungsgleichung

${\tilde{w}}^{⁗}=\mu$.

Koordinaten

Mit den neuen dimensionslosen Koordinaten und Parametern vereinfacht sich die Lösung des Problems:

So ist die analytische Lösung der Bewegungsgleichung für den Bereich i:

${\tilde{w}}_i\left(\xi \right):=\frac{\mu \cdot {\xi }^4}{24}+\frac{C_{i,3}\cdot {\xi }^3}{6}+\frac{C_{i,2}\cdot {\xi }^2}{2}+C_{i,1}\cdot \xi +C_{i,0}$

wobei der Bereich i=1 zwischen A-B sowie i=2 zwischen B-C liegt.

Die Rand- und Übergangsbedingungen lauten dann mit ℓ₂ = ℓ₁/2

$\begin{array}{ccl}{\tilde{w}}_1(0)& =& 0\\ {\tilde{w}}^{\prime }{\text{'}}_1(0)& =& 0\end{array}$, $\begin{array}{ccl}{\tilde{w}}_1(1)& =& {\tilde{w}}_2(0)\\ \tilde{w}{\text{'}}_1(1)& =& \tilde{w}{\text{'}}_2(0)\\ {\tilde{w}}^{\prime }{\text{'}}_1(1)& =& {\tilde{w}}^{\prime }{\text{'}}_2(0)\\ {\tilde{w}}^{″}{\text{'}}_1(1)& =& {\tilde{w}}^{″}{\text{'}}_2(0)\end{array}$, $\begin{array}{ccl}{\tilde{w}}_1(1/2)& =& 0\\ {\tilde{w}}^{\prime }{\text{'}}_2(1/2)& =& 0\end{array}$.

---

Links

• ...

Literature

• ...