Gelöste Aufgaben/Kig1: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
|||
| Zeile 13: | Zeile 13: | ||
<onlyinclude> | <onlyinclude> | ||
[[Datei:Kig1-01.png|200x200px|left|mini|Lageplan | [[Datei:Kig1-01.png|200x200px|left|mini|Lageplan]] | ||
Damit der Schalter zuverlässig funktioniert soll die Kraft ''F'' an der Führung so gewählt werden, dass die vorgegebene Kontaktkraft ''K'' eingestellt wird.Gesucht ist die analytische Lösung für ein Euler-Bernoulli-Modell der elastischen Struktur. | Damit der Schalter zuverlässig funktioniert soll die Kraft ''F'' an der Führung so gewählt werden, dass die vorgegebene Kontaktkraft ''K'' eingestellt wird.Gesucht ist die analytische Lösung für ein Euler-Bernoulli-Modell der elastischen Struktur. | ||
</onlyinclude> | </onlyinclude> | ||
| Zeile 117: | Zeile 117: | ||
}} | }} | ||
<table class="wikitable"> | <table class="wikitable" style="float:left;"> | ||
<tr>< | <tr><td> [[Datei:Kig1-12.png|mini|Freikörperbild]]</td></tr> | ||
<tr><td> | <tr><td>[[Datei:Kig1-17.png|mini|Freikörperbild]]</td></tr> | ||
</table> | </table> | ||
[[Datei:Kig1-14.png|mini|Rand A]] | [[Datei:Kig1-14.png|mini|Rand A]] | ||
[[Datei:Kig1-15.png|mini|Übergang B]] | [[Datei:Kig1-15.png|mini|Übergang B]] | ||
Version vom 25. März 2021, 14:12 Uhr
Aufgabenstellung
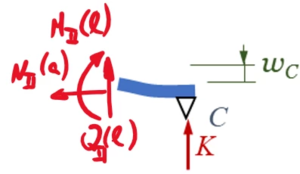
Das skizzierte System ist ein elektrischer Schalter, der in C einen Stromkreis schließen soll. Es besteht aus einem durchgehenden elastischen Stab ABC (Euler-Bernoulli-Balken: Masse m, Biegesteifigkeit EI, Länge ℓ), der in A gelenkig gelagert ist, in B mit einer Führung aus drei starren, masselosen Stäben gelenkig verbunden ist und dem Kontakt in C. Die Führung ist durch eine Feder (Steifigkeit k) mit der Umgebung verbunden.
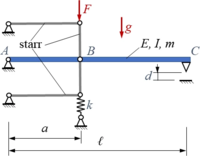
Damit der Schalter zuverlässig funktioniert soll die Kraft F an der Führung so gewählt werden, dass die vorgegebene Kontaktkraft K eingestellt wird.Gesucht ist die analytische Lösung für ein Euler-Bernoulli-Modell der elastischen Struktur.
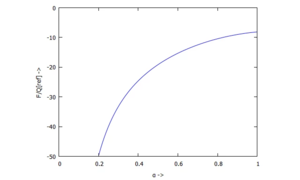
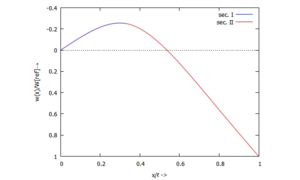
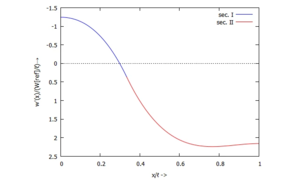
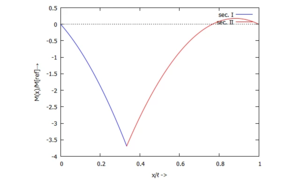
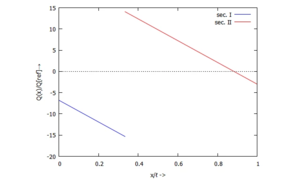
Wir lösen dazu das Gleichungssystem zur Bestimmung der Integrationskonstanten der Differentialgleichung des Euler-Bernoulli-Balkens und weiterer Unbekannten und geben die grafischen Lösungen für w, w', M und Q an.
Gegeben: K, ℓ, EI, m, g, k
Lösung mit Maxima
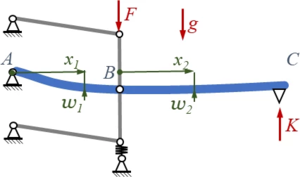
Das System besteht aus den drei starren Stäben und dem elastischen Balken.
Die Verschiebungen und Verbiegungen der Stäbe verstehen wir am besten, wenn wir uns das System einmal im ausgelenkten Zustand ansehen. Gleichgewichtsbedingungen für die Führung erhalten wir aus einfachen Kräfte- und Momentenbilanzen, die Gleichgewichtsbedingungen für den Euler-Bernoulli-Balken ist die Feld-Differentialgleichung, deren Integrationskonstanten wir an die Rand- und Übergangsbedingungen anpassen.
Aus dem Bild sehen wir
,
und wir arbeiten im folgenden mit
.
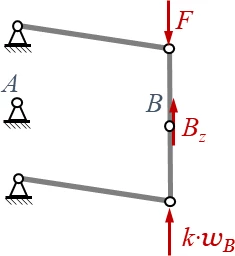
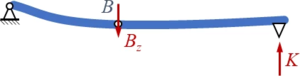
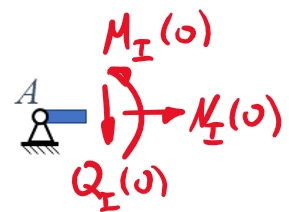
Wir beginnen, indem wir Führung und Balken von einander freischneiden:
Damit legen wir die Schnittkräfte
- Bz und
- K
frei. K ist dabei gegeben, F und Bz sind unbekannt.
Wir müssen überlegen, wo wir Bedingungen für diese beiden Größen herbekommen.
tmp
Header
Text
1+1
tmp
Integration Of Differential Equation
Text
1+1
tmp
Boundary Conditions
Text
1+1
tmp
Prepare for Solver
Text
1+1
tmp
Solving
Text
1+1
tmp
Post-Processing
Text
1+1
 |
 |
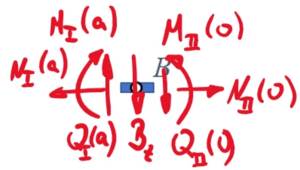
Links
- ...
Literature
- ...