Gelöste Aufgaben/JUMP/E-Motor and Drive-Train

← Back to Start

Scope

Diagram: E-Motor and Drive Train

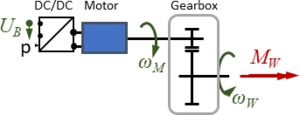
The Drive-Train consists of a DC/DC-converter, a DC Motor and a gear-box.

• DC/DC-converter: is supplied with the battery voltage U_B, the output voltage is controlled by the driver via setpoint “p“.
• motor: is a standard DC brushed motor, the manufacturer provides only few information on its characteristics - we’ll need to improvise.
• gearbox: has a gear ratio of ratio of n_G=100, its shaft rotates at speed ω_W and delivers a torque M_W to the front wheels.

The task is: provide a mathematical model for the drive train that accounts for load-alterations imposed by the driver. And we assume losses in the two converters - DC/DC and gearbox - to be negligible.

Structure

Block diagram

The drive train receives a "gas"-pedal position "p" from the driver and a battery-voltage U_B.

It delivers a torque M_W on the wheel and creates an electric current I_M through the motor.

Drive-train components.

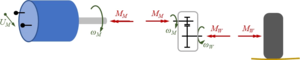
The sub-model consists of  DC/DC-converter, Motor and gear-box:

DC/DC Converter

Losses in the DC/DC converter shall be small - so for input port “1“ and output port “2“ we obtain

$U_{1}\cdot I_{1}=U_{2}\cdot I_{2}$ .

Let the “gas”-pedal-indicator “p“ control

$U_{2}=p\cdot U_{1}{\text{; }}0\leq p\leq 1.$

with

$0\leq p\leq 1{\text{ and }}U_{1}=U_{B}$

Motor

Brushed-DC motor

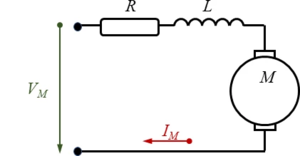
We use a common electric circuit representation for a series wound motor, the field coils are connected electrically in series with the armature coils, resistance R sums up all electrical losses in the motor.

Gearbox

Losses in the gearbox shall be small - so for input (ω_M, M_M) and output (ω_W, M_W) we obtain the fixed relation

$\omega _{M}\cdot M_{M}=\omega _{W}\cdot M_{W}$.

And we have only one differential equation for the electrical components:

${\frac {\displaystyle dI_{B}}{\displaystyle dt}}={\frac {\displaystyle U_{L}}{\displaystyle L}}$,

the remaining equations are algebraic.

Model

For the motor, we find with Kirchhoff's law that

$U_{M}=U_{R}+U_{L}+e$

with U_R, U_L being the differential voltage over resistance R and inductance L respectively. “e” is the back electromagnetic force with

$e=k_{e}\cdot \omega _{M}$

and the electromotive force constant k_e. Note the ω_M is the differential rotational velocity between rotor and stator, i.e.

$\omega _{M}={\dot {\psi }}_{W}(t)+{\dot {\phi }}(t).$

Employing

$U_{R}=R\cdot I_{M},U_{L}=L\cdot {\frac {\displaystyle dI_{M}}{\displaystyle dt}}$

and using

$M_{M}=k_{t}\cdot I_{M}$

with the armature constant k_t, we have the complete set of equations.

From the above, we find

$L\cdot {\frac {\displaystyle d}{\displaystyle dt}}{I_{M}}(t)=U_{B}(t)\cdot p(t)-R\,{I_{M}}(t)-e$

and additionally the algebraic equations

${\begin{array}{ll}{I_{B}}&={I_{M}}\cdot \operatorname {p} (t),\\{U_{R}}&=R\cdot {I_{M}}(t),\\{U_{L}}&={U_{B}}\cdot \operatorname {p} (t)-R\cdot {I_{M}}(t)-e,\\{U_{M}}&={U_{B}}\cdot \operatorname {p} (t)\end{array}}$.

tmp

Electrical Components

Text

1+1=2

tmp

Mechanical Components

Text

1+1=2

Parameter

---

>

Back to Start →

---

References

• ...