Gelöste Aufgaben/JUMP/Driver Controls

← Back to Start

Driver Controls

Since we’re in a 2D-simulation environment, the driver controls only “gas” (acceleration) and breaks - no directional control needed to be taken into account.

Scope

Block diagram

The track poses challenges that require the driver to control the driving and breaking torque on the wheel. These track-specific challenges include

• achieving maximum acceleration, thus avoiding wheel-skid and adjusting to a slip that provides optimal traction,
• achieving maximum deceleration when breaking and therefore avoiding wheels becoming locked,
• avoiding excessive battery-temperatures and thus controlling driving torque.

Structure

The driver is tasked to control wheel slip and wheel skid via the "gas"-pedal. We differentiate between

• slip as the relative micro-velocity necessary to transmit forces in rolling contact and
• skip as unwanted excessive relative velocity resulting from poor torque-control at the wheels.

The information for this task come as "info" from the car's motion.

Friction characteristic and desired skid-velocity-range.

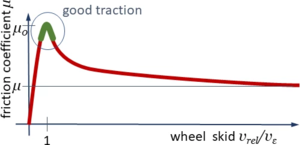
To avoid wheel skid and to control slip, the driver will aim to maintain a relative velocity at the wheel-contact point “C“ around the small velocity v_ε, thus reducing torque M_W if v_rel > v_ε and increasing M_W if v_rel < v_ε.

This is a very challenging system to be controlled because

• the velocity domain that we target is rather small and
• the characteristic for v_rel > v_ε is degressive: the friction force decreases with relative velocity.

Model

The most common controller in technical applications is a PID-controller. Our target value to control is v_rel, our set-point is

$r:=v_{\epsilon }$ .

and we define the error value e as

${\begin{array}{ll}e&=f({\tilde {v}}){\text{ with }}{\tilde {v}}={\frac {\displaystyle v_{rel}}{\displaystyle v_{\varepsilon }}};{\text{ here we choose }}\\&=1-{\tilde {v}}\end{array}}$ .

The function for e ensures that "p" increases if v_rel < v_ε and decreases otherwise.

Block-diagram controller

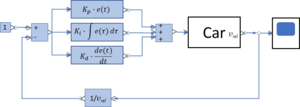
With controller parameters K_p, Ki, K_d we get this diagram for the controlled system.

The controller adds thus adds the state variable

$E_{I}:=\displaystyle \int _{0}^{t}e(\tau )d\tau$

to the system. And we need to find

${\begin{array}{ll}{\dot {e}}&={\frac {\displaystyle de(t)}{\displaystyle dt}}\\&={\frac {\displaystyle 1}{\displaystyle v_{red}}}\cdot {\frac {\displaystyle dv_{rel}(t)}{\displaystyle dt}}\\\end{array}}$

as the rate of change from the Car-Body-Model.

So the only state variable from the driver is

${\underline {q}}_{D}(t)=\left(E(t)\right)$ .

The output "p" of the submodel is not a state variable, but

$p(t)=K_{p}\cdot e(t)+K_{i}\cdot E(t)+K_{d}\cdot {\dot {e}}(t)$

Variables

name	symbol	unit
integrator part of PID controller	E(t)	1

Parameter

name	symbol	unit
coefficient of proportional contribution	Kp	1/s
coefficient of integrator contribution	Ki	1/s^2
coefficient of differential contribution	Kd	1

next workpackage: e-motor and drive-train →

---

References

1. Yuan, Lei; Chen, Hong; Ren, Bingtao; Zhao, Haiyan: Model predictive slip control for electric vehicle with four in-wheel motors, Proceedings of the 34th Chinese Control Conference July 28-30, 2015, Hangzhou, China, p 7895-7900
2. ...