Gelöste Aufgaben/JUMP/Driver Controls: Unterschied zwischen den Versionen
| Zeile 14: | Zeile 14: | ||
==Structure== | ==Structure== | ||
[[Datei:JUMP-driver- | The driver is tasked to control wheel slip and wheel skid via the "gas"-pedal. We differentiate between | ||
* '''slip''' as the relative micro-velocity necessary to transmit forces in rolling contact and | |||
* '''skip''' as unwanted excessive relative velocity resulting from poor torque-control at the wheels. | |||
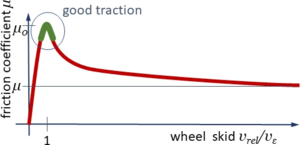
The information for this task come as "''info''" from the car's motion.[[Datei:JUMP-driver-frictioncharacteristic.png|mini|Friction characteristic and desired skid-velocity-range.]]To avoid wheel skid and to control slip, the driver will aim to maintain a relative velocity at the wheel-contact point “C“ around the small velocity ''v<sub>ε</sub>'', thus reducing torque ''M<sub>W</sub>'' if ''v<sub>rel</sub>'' > ''v<sub>ε</sub>'' and increasing ''M<sub>W</sub>'' if ''v<sub>rel</sub>'' < ''v<sub>ε</sub>''. | |||
This is a very challenging system to be controlled because | |||
* the velocity domain that we target is rather small and | |||
* the characteristic for ''v<sub>rel</sub>'' > ''v<sub>ε</sub>'' is degressive: the friction force decreases with relative velocity. | |||
==Model== | ==Model== | ||
[[Datei:JUMP-driver- | The most common controller in technical applications is a PID-controller. Our target value to control is ''v<sub>rel</sub>'', our set-point is | ||
<math>r := v_\epsilon</math> . | |||
and we define the error value e as | |||
<math>\begin{array}{ll} | |||
e &= f(\tilde{v}) \text{ with } \tilde{v} = \frac{\displaystyle v_{rel}}{\displaystyle v_{\varepsilon}}; \text{ here we choose }\\ | |||
&= 1-\tilde{v} | |||
\end{array}</math> . | |||
The function for ''e'' ensures that "''p"'' increases if ''v<sub>rel</sub>'' < ''v<sub>ε</sub>'' and decreases otherwise. [[Datei:JUMP-driver-blockdiagram-controller.png|mini|Block-diagram controller]]With controller parameters ''K<sub>p</sub>, Ki, K<sub>d</sub>'' we get this diagram for the controlled system. | |||
The controller adds thus adds the state variable | |||
<math>E_I := \displaystyle \int_0^t e(\tau) d\tau</math> | |||
to the system. And we need to find | |||
<math>\begin{array}{ll} | |||
\dot{e} &= \frac{\displaystyle d e(t)}{\displaystyle d t}\\ | |||
&=\frac{\displaystyle 1}{\displaystyle v_{red}} \cdot \frac{\displaystyle d v_{rel}(t)}{\displaystyle d t}\\ | |||
\end{array}</math> | |||
as the rate of change from the [[Gelöste Aufgaben/JUMP/Car-Body|Car-Body]]-Model. | |||
So the only state variable from the driver is | |||
<math>\underline{q}_D(t) = \left(E(t)\right)</math> . | |||
The output "p" of the submodel is not a state variable, but | |||
<math>p(t) = K_p\cdot e(t) + K_i\cdot E(t) + K_d\cdot \dot{e}(t) </math> | |||
==Variables== | ==Variables== | ||
{| class="wikitable" | |||
!name | |||
!symbol | |||
!unit | |||
|- | |||
|integrator part of PID controller | |||
|E(t) | |||
|1 | |||
|} | |||
==Parameter== | == Parameter == | ||
{| class="wikitable" | |||
--- | !name | ||
!symbol | |||
!unit | |||
|- | |||
|coefficient of proportional contribution | |||
|''K<sub>p</sub>'' | |||
|1/s | |||
|- | |||
|coefficient of integrator contribution | |||
|''K<sub>i</sub>'' | |||
|1/s^2 | |||
|- | |||
|coefficient of differential contribution | |||
|''K<sub>d</sub>'' | |||
|1 | |||
|} | |||
[[Gelöste Aufgaben/JUMP/E-Motor and Drive-Train|next workpackage: e-motor and drive-train →]] | [[Gelöste Aufgaben/JUMP/E-Motor and Drive-Train|next workpackage: e-motor and drive-train →]] | ||
| Zeile 29: | Zeile 95: | ||
<hr/> | <hr/> | ||
'''References''' | '''References''' | ||
# Yuan, Lei; Chen, Hong; Ren, Bingtao; Zhao, Haiyan: Model predictive slip control for electric vehicle with four in-wheel motors, Proceedings of the 34th Chinese Control Conference July 28-30, 2015, Hangzhou, China, p 7895-7900 | |||
# ... | |||
Version vom 10. März 2021, 14:10 Uhr

Since we’re in a 2D-simulation environment, the driver controls only “gas” (acceleration) and breaks - no directional control needed to be taken into account.
Scope

The track poses challenges that require the driver to control the driving and breaking torque on the wheel. These track-specific challenges include
- achieving maximum acceleration, thus avoiding wheel-skid and adjusting to a slip that provides optimal traction,
- achieving maximum deceleration when breaking and therefore avoiding wheels becoming locked,
- avoiding excessive battery-temperatures and thus controlling driving torque.
Structure
The driver is tasked to control wheel slip and wheel skid via the "gas"-pedal. We differentiate between
- slip as the relative micro-velocity necessary to transmit forces in rolling contact and
- skip as unwanted excessive relative velocity resulting from poor torque-control at the wheels.
The information for this task come as "info" from the car's motion.
To avoid wheel skid and to control slip, the driver will aim to maintain a relative velocity at the wheel-contact point “C“ around the small velocity vε, thus reducing torque MW if vrel > vε and increasing MW if vrel < vε.
This is a very challenging system to be controlled because
- the velocity domain that we target is rather small and
- the characteristic for vrel > vε is degressive: the friction force decreases with relative velocity.
Model
The most common controller in technical applications is a PID-controller. Our target value to control is vrel, our set-point is
.
and we define the error value e as
.
The function for e ensures that "p" increases if vrel < vε and decreases otherwise.
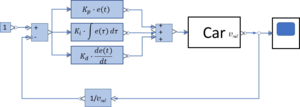
With controller parameters Kp, Ki, Kd we get this diagram for the controlled system.
The controller adds thus adds the state variable
to the system. And we need to find
as the rate of change from the Car-Body-Model.
So the only state variable from the driver is
.
The output "p" of the submodel is not a state variable, but
Variables
| name | symbol | unit |
|---|---|---|
| integrator part of PID controller | E(t) | 1 |
Parameter
| name | symbol | unit |
|---|---|---|
| coefficient of proportional contribution | Kp | 1/s |
| coefficient of integrator contribution | Ki | 1/s^2 |
| coefficient of differential contribution | Kd | 1 |
next workpackage: e-motor and drive-train →
References
- Yuan, Lei; Chen, Hong; Ren, Bingtao; Zhao, Haiyan: Model predictive slip control for electric vehicle with four in-wheel motors, Proceedings of the 34th Chinese Control Conference July 28-30, 2015, Hangzhou, China, p 7895-7900
- ...