Gelöste Aufgaben/JUMP/Car-Body: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
|||
| Zeile 89: | Zeile 89: | ||
The track-polynomials are | The track-polynomials are | ||
<math>\begin{array}{ll} | ::<math>\begin{array}{ll} | ||
t_i(x) &= y_i \cdot \tilde{x}_i + y_{i-1}\cdot \left(1- \tilde{x}_i \right) \text{ for } \tilde{x}_i = \frac{\displaystyle x - x_{i-1}}{\displaystyle x_i - x_{i-1}}\\ | t_i(x) &= y_i \cdot \tilde{x}_i + y_{i-1}\cdot \left(1- \tilde{x}_i \right) \text{ for } \tilde{x}_i = \frac{\displaystyle x - x_{i-1}}{\displaystyle x_i - x_{i-1}}\\ | ||
&=T_{i,1}\cdot x + T_{i,0} | &=T_{i,1}\cdot x + T_{i,0} | ||
| Zeile 96: | Zeile 96: | ||
During the numerical integration of the initial-value-problem - when the car runs along the track - the solver needs to cope with the transition between two straight lines - which is numerically more efficient if we convert the road in a continuously differentiable function. [[Datei:JUMP-carbody-track-rounding.png|mini|Rounding the edges.]]For this purpose, we define transition polynomials ''p<sub>i</sub>'' of second degree - parabolas - as | During the numerical integration of the initial-value-problem - when the car runs along the track - the solver needs to cope with the transition between two straight lines - which is numerically more efficient if we convert the road in a continuously differentiable function. [[Datei:JUMP-carbody-track-rounding.png|mini|Rounding the edges.]]For this purpose, we define transition polynomials ''p<sub>i</sub>'' of second degree - parabolas - as | ||
<math>p_i(x) = \displaystyle \sum_{j=0}^2 P_{i,j}\cdot x^j</math> | ::<math>p_i(x) = \displaystyle \sum_{j=0}^2 P_{i,j}\cdot x^j</math> | ||
which connect two neighboring tracks. | which connect two neighboring tracks. | ||
| Zeile 102: | Zeile 102: | ||
The boundary conditions for the parabolas (red) and the neighboring lines (blue) yield | The boundary conditions for the parabolas (red) and the neighboring lines (blue) yield | ||
<math>\begin{array}{ll} | ::<math>\begin{array}{ll} | ||
\color{blue} t_i(x_i-\Delta x_i) &= \color{red} p_{i}(x_i-\Delta x_i),\\ | \color{blue} t_i(x_i-\Delta x_i) &= \color{red} p_{i}(x_i-\Delta x_i),\\ | ||
\color{blue} | \color{blue} | ||
| Zeile 117: | Zeile 117: | ||
And though we have four boundary conditions, they allow for a solution with three unknown polynomial coefficients ''P<sub>i</sub>'' if ''Δx<sub>i</sub>'' is identical left and right from ''x<sub>i</sub>'' - which we have already implied. | And though we have four boundary conditions, they allow for a solution with three unknown polynomial coefficients ''P<sub>i</sub>'' if ''Δx<sub>i</sub>'' is identical left and right from ''x<sub>i</sub>'' - which we have already implied. | ||
<math>\begin{array}{ll} | ::<math>\begin{array}{ll} | ||
{b_3}&=0,\\ | {b_3}&=0,\\ | ||
{b_2}&=\frac{\displaystyle {a_{2,1}}-{a_{1,1}}}{\displaystyle 4 \mathit{\Delta x_i}},\\ | {b_2}&=\frac{\displaystyle {a_{2,1}}-{a_{1,1}}}{\displaystyle 4 \mathit{\Delta x_i}},\\ | ||
| Zeile 126: | Zeile 126: | ||
and | and | ||
<math>\begin{array}{ll} | ::<math>\begin{array}{ll} | ||
{a_{1,0}}&={y_i}-{x_i}\, {a_{1,1}},\\ | {a_{1,0}}&={y_i}-{x_i}\, {a_{1,1}},\\ | ||
{a_{1,1}}&=\frac{\displaystyle {y_{i-1}}-{y_i}}{\displaystyle {x_{i-1}}-{x_i}}\operatorname{,}\\ | {a_{1,1}}&=\frac{\displaystyle {y_{i-1}}-{y_i}}{\displaystyle {x_{i-1}}-{x_i}}\operatorname{,}\\ | ||
| Zeile 140: | Zeile 140: | ||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
1+1=2 | /*******************************************************/ | ||
/* MAXIMA script */ | |||
/* version: wxMaxima 16.04.2 */ | |||
/* author: Andreas Baumgart */ | |||
/* last updated: 2021-02-08 */ | |||
/* ref: Modelling and Simulation (TUAS) */ | |||
/* description: Rounding between straight line-segments*/ | |||
/*******************************************************/ | |||
/*******************************************************/ | |||
/* declarations */ | |||
/*******************************************************/ | |||
declare("Δ",alphabetic); | |||
params: [x[0] = 0, x[1] = 10, x[2]=15, | |||
y[0] = 0, y[1] = 1, y[2]=-1, | |||
eps = 0.2]; | |||
/*******************************************************/ | |||
/* polynomials */ | |||
/*******************************************************/ | |||
/* polynomial coefficiets of two consecutive straigt lines */ | |||
P : [[a[1,1],a[1,0]],[a[2,1],a[2,0]]]; | |||
/* polynomials of cubic and two consecutive linear polynomials */ | |||
p : [a[1,1]*x+a[1,0], | |||
b[3]*x^3+b[2]*x^2+b[1]*x+b[0], | |||
a[2,1]*x+a[2,0]]; | |||
/* compute polynomial coefficients from (x[i]/y[i])-points*/ | |||
linear : solve([subst([x=x[0]],p[1]) = y[0], | |||
subst([x=x[1]],p[1]) = y[1], | |||
subst([x=x[1]],p[3]) = y[1], | |||
subst([x=x[2]],p[3]) = y[2]], [a[1,0],a[1,1],a[2,0],a[2,1]])[1]; | |||
/* equations to continuously fit cubic function to lines */ | |||
equs : [subst([x=x[1]-Δx], p[1]) = subst([x=x[1]-Δx], p[2]), | |||
subst([x=x[1]+Δx], p[3]) = subst([x=x[1]+Δx], p[2]), | |||
subst([x=x[1]-Δx], diff(p[1],x)) = subst([x=x[1]-Δx], diff(p[2],x)), | |||
subst([x=x[1]+Δx], diff(p[3],x)) = subst([x=x[1]+Δx], diff(p[2],x))]; | |||
/* unknowns */ | |||
Q : [b[3],b[2],b[1],b[0]]; | |||
/* solve for unknowns */ | |||
sol : ratsimp(subst(linear,solve(equs,Q)[1])); | |||
/* solve linear system of equations for unknown coefficients */ | |||
ACM : augcoefmatrix(equs,Q); | |||
print(submatrix(ACM,5)," * ",transpose(Q)," = ",col(ACM,5))$ | |||
/* or - more simple when doing it numerically .... */ | |||
/* coefficients of straigt line polynomials */ | |||
s : makelist(a[i,1] = (y[i-1]-y[i])/(x[i-1]-x[i]),i,1,2); | |||
P : [[a[1,1],a[1,0]],[a[2,1],a[2,0]]]; | |||
p : [a[1,1]*x+a[1,0], | |||
b[3]*x^3+b[2]*x^2+b[1]*x+b[0], | |||
a[2,1]*x+a[2,0]]; | |||
linear : solve([subst([x=x[1]],p[1]) = y[1], | |||
subst([x=x[1]],p[3]) = y[1]], [a[1,0],a[2,0]])[1]; | |||
equs : [subst([x=x[1]-Δx], p[1]) = subst([x=x[1]-Δx], p[2]), | |||
subst([x=x[1]+Δx], p[3]) = subst([x=x[1]+Δx], p[2]), | |||
subst([x=x[1]-Δx], diff(p[1],x)) = subst([x=x[1]-Δx], diff(p[2],x)), | |||
subst([x=x[1]+Δx], diff(p[3],x)) = subst([x=x[1]+Δx], diff(p[2],x))]; | |||
Q : [b[3],b[2],b[1],b[0]]; | |||
sol : ratsimp(subst(linear,solve(equs,Q)))[1]; | |||
/* check with parameters */ | |||
subst(params,subst(s,subst(linear,solve(equs,Q)))); | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
| Zeile 147: | Zeile 218: | ||
<!-------------------------------------------------------------------------> | <!-------------------------------------------------------------------------> | ||
==tmp== | ==tmp== | ||
{{MyCodeBlock | {{MyCodeBlock | ||
Version vom 10. März 2021, 12:55 Uhr
Scope
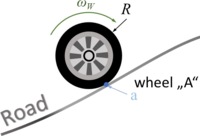
In common simulation applications - especially for full-size commercial cars - the pitch-angle of the car is assumed to be small to allow for a linearization of geometry and most parts of the equations of motion. We drop this limitation so we can do more fancy stuff with our model - like climbing steep roads or jumping across ditches.
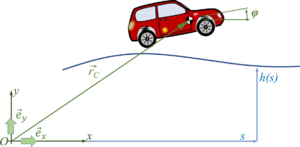
We employ a spatial x-y coordinate system, x in horizontal, y in vertical, upwards direction. And we’ll briefly employ the z-axis as rotation direction - which is towards you following the “right-hand-rule“ for coordinate systems.
Structure
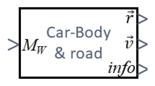
The driver controls the car's motion via the position of the "gas"-pedal, which is being translated into a torque MW at the wheel.
This toque will change velocities and thus the position of the car. These state-variables will then create - via info - a feedback to the driver.
We’ll need to invest significant efforts in describing the kinematics of the car-motion and to derive its equations of body-motion since we do not want to limit our study on small pitch-angles of the car. Key accessory will be vectors, which map locations like the center of mass:
- .
This vector has - in 2D - two coordinates , measured in the inertial x-y frame:
- with .
representing the unit vectors spanning the x-y space. If we refer to a specific frame, we may drop the vector-notation and refer to the column-matrix of coordinates only, so
- .
We’ll also employ coordinate transformations using Euler-rotations.
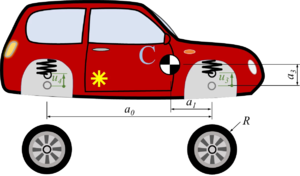
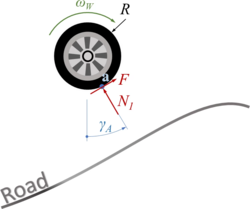
The car with front-wheel drive consists of the car-body with center of mass “C“, the front wheels “A“ and the rear wheel “B“. Masses of car-body and wheel-sets are M and m respectively.The geometry of the car is described by
- a0: the wheel base;
- a1: longitudinal distance between center of mass and front-wheel-hub;
- a2 = a0 - a1 and
- a3: vertical distance between center of mass and front-wheel-hub (relaxed springs).
tmp
Body
We use five coordinates to describe the motion of the car:
- for the location of the center of mass of the car-body and its pitch-angle
 ,
, - for the "vertical" motion of the wheel hubs relative to the car-body - which is synonym to the compression of the springs
and - as the rotation angle of the front-wheel - we'll not account for the rotation of the rear-wheel.
So the center of mass of the car-body is
- ,
the coordinate system of the car is
where
- .
So the location of the front-wheel “A“ is
or
- .
Likewise, the location of the rear-wheel “B“ is
and in the following, we’ll be using the abbreviations
and
- .
tmp
Track
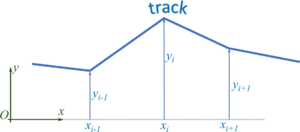
We describe the road by road-sections, which we call tracks. We start by defining each track as a line-segment, i.e. a first-order polynomial. The road is thus defined by pairs of track-endpoints, i.e. (xi, yi).
The track-polynomials are
- .
During the numerical integration of the initial-value-problem - when the car runs along the track - the solver needs to cope with the transition between two straight lines - which is numerically more efficient if we convert the road in a continuously differentiable function.
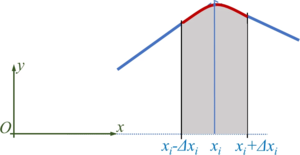
For this purpose, we define transition polynomials pi of second degree - parabolas - as
which connect two neighboring tracks.
The boundary conditions for the parabolas (red) and the neighboring lines (blue) yield
And though we have four boundary conditions, they allow for a solution with three unknown polynomial coefficients Pi if Δxi is identical left and right from xi - which we have already implied.
and
But instead of employing the above, we solve the linear systems of equations for the coefficients numerically.
Now each polynomial creates new endpoints xi - Δxi and xi + Δxi which substitute for the initial xi-point. The tracks are represented by a succession of lines and parabolas.
Next we need to find the contact point between wheel and road!
/*******************************************************/
/* MAXIMA script */
/* version: wxMaxima 16.04.2 */
/* author: Andreas Baumgart */
/* last updated: 2021-02-08 */
/* ref: Modelling and Simulation (TUAS) */
/* description: Rounding between straight line-segments*/
/*******************************************************/
/*******************************************************/
/* declarations */
/*******************************************************/
declare("Δ",alphabetic);
params: [x[0] = 0, x[1] = 10, x[2]=15,
y[0] = 0, y[1] = 1, y[2]=-1,
eps = 0.2];
/*******************************************************/
/* polynomials */
/*******************************************************/
/* polynomial coefficiets of two consecutive straigt lines */
P : [[a[1,1],a[1,0]],[a[2,1],a[2,0]]];
/* polynomials of cubic and two consecutive linear polynomials */
p : [a[1,1]*x+a[1,0],
b[3]*x^3+b[2]*x^2+b[1]*x+b[0],
a[2,1]*x+a[2,0]];
/* compute polynomial coefficients from (x[i]/y[i])-points*/
linear : solve([subst([x=x[0]],p[1]) = y[0],
subst([x=x[1]],p[1]) = y[1],
subst([x=x[1]],p[3]) = y[1],
subst([x=x[2]],p[3]) = y[2]], [a[1,0],a[1,1],a[2,0],a[2,1]])[1];
/* equations to continuously fit cubic function to lines */
equs : [subst([x=x[1]-Δx], p[1]) = subst([x=x[1]-Δx], p[2]),
subst([x=x[1]+Δx], p[3]) = subst([x=x[1]+Δx], p[2]),
subst([x=x[1]-Δx], diff(p[1],x)) = subst([x=x[1]-Δx], diff(p[2],x)),
subst([x=x[1]+Δx], diff(p[3],x)) = subst([x=x[1]+Δx], diff(p[2],x))];
/* unknowns */
Q : [b[3],b[2],b[1],b[0]];
/* solve for unknowns */
sol : ratsimp(subst(linear,solve(equs,Q)[1]));
/* solve linear system of equations for unknown coefficients */
ACM : augcoefmatrix(equs,Q);
print(submatrix(ACM,5)," * ",transpose(Q)," = ",col(ACM,5))$
/* or - more simple when doing it numerically .... */
/* coefficients of straigt line polynomials */
s : makelist(a[i,1] = (y[i-1]-y[i])/(x[i-1]-x[i]),i,1,2);
P : [[a[1,1],a[1,0]],[a[2,1],a[2,0]]];
p : [a[1,1]*x+a[1,0],
b[3]*x^3+b[2]*x^2+b[1]*x+b[0],
a[2,1]*x+a[2,0]];
linear : solve([subst([x=x[1]],p[1]) = y[1],
subst([x=x[1]],p[3]) = y[1]], [a[1,0],a[2,0]])[1];
equs : [subst([x=x[1]-Δx], p[1]) = subst([x=x[1]-Δx], p[2]),
subst([x=x[1]+Δx], p[3]) = subst([x=x[1]+Δx], p[2]),
subst([x=x[1]-Δx], diff(p[1],x)) = subst([x=x[1]-Δx], diff(p[2],x)),
subst([x=x[1]+Δx], diff(p[3],x)) = subst([x=x[1]+Δx], diff(p[2],x))];
Q : [b[3],b[2],b[1],b[0]];
sol : ratsimp(subst(linear,solve(equs,Q)))[1];
/* check with parameters */
subst(params,subst(s,subst(linear,solve(equs,Q))));
tmp
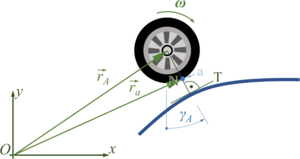
Contact-Point and -Normal
Text
1+1=2
tmp
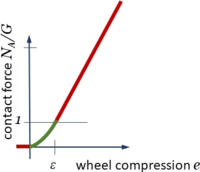
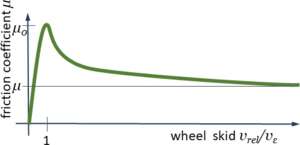
Contact Forces
Text
1+1=2
tmp
Track
Text
1+1=2
tmp
Track
Text
1+1=2
tmp
Track
Text
1+1=2
tmp
Track
Text
1+1=2
Variables
Parameter
x
y
z
a
b
c
next workpackage: driver-controls →
References
- ...