Gelöste Aufgaben/JUMP/Car-Body: Unterschied zwischen den Versionen
| Zeile 34: | Zeile 34: | ||
<ul> | <ul> | ||
<li><math>u_1(t), u_2(t), \varphi(t)</math> for the location of the center of mass of the car-body and its pitch-angle<br/> | <li><math>u_1(t), u_2(t), \varphi(t)</math> for the location of the center of mass of the car-body and its pitch-angle<br/> [[Datei:JUMP-carbody-slide3.png|alternativtext=|rahmenlos]],</li> | ||
<li><math>u_3, u_4</math> for the "vertical" motion of the wheel hubs relative to the car-body - which is synonym to the compression of the springs <br/> | <li><math>u_3, u_4</math> for the "vertical" motion of the wheel hubs relative to the car-body - which is synonym to the compression of the springs <br/> [[Datei:JUMP-carbody-slide4.png|alternativtext=|rahmenlos]]<br/> and</li> | ||
<li><math>\psi(t)</math> as the rotation angle of the front-wheel - we'll not account for the rotation of the rear-wheel.</li> | <li><math>\psi(t)</math> as the rotation angle of the front-wheel - we'll not account for the rotation of the rear-wheel.</li> | ||
</ul> | </ul> | ||
| Zeile 41: | Zeile 41: | ||
So the center of mass of the car-body is | So the center of mass of the car-body is | ||
<math>\vec{r}_M = \vec{\underline{e}}_0\cdot\left(\begin{array}{c}u_1(t)\\u_2(t)\end{array}\right)</math>, | ::<math>\vec{r}_M = \vec{\underline{e}}_0\cdot\left(\begin{array}{c}u_1(t)\\u_2(t)\end{array}\right)</math>, | ||
the coordinate system of the car is | the coordinate system of the car is | ||
<math>\vec{\underline{e}}_C = \vec{\underline{e}}_0 \cdot \underline{\underline{D}}(\varphi(t))</math> | ::<math>\vec{\underline{e}}_C = \vec{\underline{e}}_0 \cdot \underline{\underline{D}}(\varphi(t))</math> | ||
where | where | ||
<math>\underline{\underline{D}}(\varphi) = \left( \begin{array}{rr} | ::<math>\underline{\underline{D}}(\varphi) = \left( \begin{array}{rr} | ||
\cos(\varphi)&-\sin(\varphi)\\ | \cos(\varphi)&-\sin(\varphi)\\ | ||
+\sin(\varphi)&\cos(\varphi)\\ | +\sin(\varphi)&\cos(\varphi)\\ | ||
| Zeile 56: | Zeile 56: | ||
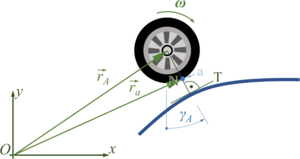
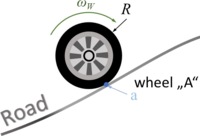
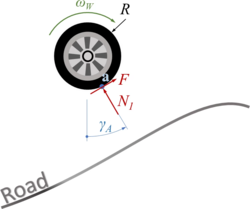
So the location of the front-wheel “''A''“ is | So the location of the front-wheel “''A''“ is | ||
<math>\vec{r}_A = \vec{r}_M + \vec{r}_{MA}</math> | ::<math>\vec{r}_A = \vec{r}_M + \vec{r}_{MA}</math> | ||
or | or | ||
<math>\underline{r}_A = \underline{r}_M + \underline{\underline{D}}(\varphi(t)) \cdot \left(\begin{array}{c}a_1\\-a_3+u_3(t)\end{array}\right)</math>. | ::<math>\underline{r}_A = \underline{r}_M + \underline{\underline{D}}(\varphi(t)) \cdot \left(\begin{array}{c}a_1\\-a_3+u_3(t)\end{array}\right)</math>. | ||
Likewise, the location of the rear-wheel “''B''“ is | Likewise, the location of the rear-wheel “''B''“ is | ||
<math>\underline{r}_B = \underline{r}_M + \underline{\underline{D}}(\varphi(t)) \cdot \left(\begin{array}{c}- a_2\\-a_3+u_4(t)\end{array}\right)</math> | ::<math>\underline{r}_B = \underline{r}_M + \underline{\underline{D}}(\varphi(t)) \cdot \left(\begin{array}{c}- a_2\\-a_3+u_4(t)\end{array}\right)</math> | ||
and in the following, we’ll be using the abbreviations | and in the following, we’ll be using the abbreviations | ||
<math>\left(\begin{array}{c}U_3\\U_4\end{array}\right) =: \underline{r}_A</math> | ::<math>\left(\begin{array}{c}U_3\\U_4\end{array}\right) =: \underline{r}_A</math> | ||
and | and | ||
<math>\left(\begin{array}{c}U_5\\U_6\end{array}\right) =: \underline{r}_B</math>. | ::<math>\left(\begin{array}{c}U_5\\U_6\end{array}\right) =: \underline{r}_B</math>. | ||
==Variables== | ==Variables== | ||
Version vom 10. März 2021, 11:04 Uhr
Scope
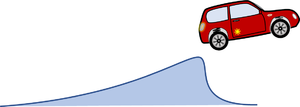
In common simulation applications - especially for full-size commercial cars - the pitch-angle of the car is assumed to be small to allow for a linearization of geometry and most parts of the equations of motion. We drop this limitation so we can do more fancy stuff with our model - like climbing steep roads or jumping across ditches.
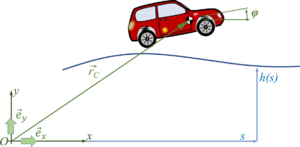
We employ a spatial x-y coordinate system, x in horizontal, y in vertical, upwards direction. And we’ll briefly employ the z-axis as rotation direction - which is towards you following the “right-hand-rule“ for coordinate systems.
Structure
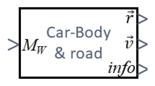
The driver controls the car's motion via the position of the "gas"-pedal, which is being translated into a torque MW at the wheel.
This toque will change velocities and thus the position of the car. These state-variables will then create - via info - a feedback to the driver.
We’ll need to invest significant efforts in describing the kinematics of the car-motion and to derive its equations of body-motion since we do not want to limit our study on small pitch-angles of the car. Key accessory will be vectors, which map locations like the center of mass:
- .
This vector has - in 2D - two coordinates , measured in the inertial x-y frame:
- with .
representing the unit vectors spanning the x-y space. If we refer to a specific frame, we may drop the vector-notation and refer to the column-matrix of coordinates only, so
- .
We’ll also employ coordinate transformations using Euler-rotations.
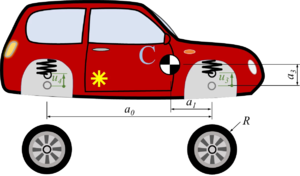
The car with front-wheel drive consists of the car-body with center of mass “C“, the front wheels “A“ and the rear wheel “B“. Masses of car-body and wheel-sets are M and m respectively.The geometry of the car is described by
- a0: the wheel base;
- a1: longitudinal distance between center of mass and front-wheel-hub;
- a2 = a0 - a1 and
- a3: vertical distance between center of mass and front-wheel-hub (relaxed springs).
Model
We use five coordinates to describe the motion of the car:
- for the location of the center of mass of the car-body and its pitch-angle
 ,
, - for the "vertical" motion of the wheel hubs relative to the car-body - which is synonym to the compression of the springs
and - as the rotation angle of the front-wheel - we'll not account for the rotation of the rear-wheel.
So the center of mass of the car-body is
- ,
the coordinate system of the car is
where
- .
So the location of the front-wheel “A“ is
or
- .
Likewise, the location of the rear-wheel “B“ is
and in the following, we’ll be using the abbreviations
and
- .
Variables
Parameter
x
y
z
a
b
c
next workpackage: driver-controls →
References
- ...