Gelöste Aufgaben/FEB1: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 23: | Zeile 23: | ||
==tmp== | ==tmp== | ||
<!-------------------------------------------------------------------------------->{{MyCodeBlock|title=Header | <!--------------------------------------------------------------------------------> | ||
Zu diesem Problem finden wir einfach eine analytische Lösung - die nutzen wir später, um unsere Ergebnisse dimensionslos zu machen. | |||
Ausgangspunkt ist die Gleichgewichtsbeziehung des [[Sources/Lexikon/Dehnstab|Dehnstabes]]. Die Streckenlast ''n'' (hier ''n(r)'') ist die Zentrifugalkraft - oder die [[Sources/Lexikon/D'Alembert'sche Trägheitskraft|D'Alembert'sche Trägheitskraft]] der Zentripetalbeschleunigung, also | |||
<math>n(x) = -\varrho\,A\,r\,\Omega^2</math> . | |||
Die Bewegungsgleichung lautet dann | |||
<math>E\,A\,u''(r) = \varrho\,A\,r\,\Omega^2</math> . | |||
Die allgemeine Lösung ist | |||
<math>\displaystyle A\,E\,u(r)=-\frac{\varrho\,A\,{{\Omega}^{2}}\,{{r}^{3}}}{6}+{{c}_{1}}r+{{c}_{0}}</math> , | |||
angepasst an die Randbedingungen | |||
<math>\begin{array}{l}u(0) = 0\\\displaystyle E\,A\,\frac{d}{dr}u|_{r=\ell_0} = 0\end{array}</math> | |||
erhalten wir | |||
<math>\displaystyle {u}(r)=\frac{3{{\ell}_{0}^{2}}\,r-r^3}{6\,A\,E}\cdot \varrho\,A\,{{\Omega}^{2}}</math> . | |||
Als Bezugslänge gewinnen wir hier | |||
<math>\begin{array}{ll}u_s &= u(\ell_0)\\&\displaystyle=\frac{{{\ell}_{0}^{3}}\,{{\Omega}^{2}}\varrho}{3E}\end{array}</math>{{MyCodeBlock|title=Header | |||
|text=Text | |text=Text | ||
|code= | |code= | ||
| Zeile 32: | Zeile 58: | ||
==tmp== | ==tmp== | ||
<!-------------------------------------------------------------------------------->{{MyCodeBlock|title=Declarations | <!-------------------------------------------------------------------------------->Für die Komposition der Bewegungsgleichungen brauchen wir die Element-Steifigkeitsmatrix und die Element-Lastmatrix. | ||
Wir gehen von gleichlangen Elementen aus, hier von | |||
<math>I =4</math> | |||
Elementen, also | |||
<math>\displaystyle \ell_i = \frac{\ell_0}{I}</math>. | |||
Wie im Abschnitt "[[Randwertprobleme/Methoden zur Lösung von Randwertproblemen/Finite Elemente Methode|Finite Elemente Methode]]" verwenden wir die linearen Ansatzfunktionen | |||
<math>\phi_1 = 1-\xi \; \text{ und }\;\phi_1 = \xi</math>, | |||
also | |||
<math>u_i(\xi_i) = U_{i-1} \cdot \phi_1(\xi_1) + U_{i} \cdot \phi_2(\xi_i)</math>. | |||
Die Element-Steifigkeitsmatrix ergibt sich für den Dehnstab zu | |||
<math>\displaystyle \underline{\underline{K}}_i = \frac{E\,A}{\ell_i}\cdot\left( \begin{array}{rr}1&-1\\-1&1\end{array}\right)</math>. | |||
Die Element-Lastmatrix ist etwas schwieriger. Für ein einzelnes Element ''i'' ist | |||
<math>\displaystyle \delta W^a = \int_{\displaystyle r_i-1}^{\displaystyle r_{i}} \varrho\,A\,r\,\Omega^2 \cdot \delta u(r)\;dr</math>. | |||
Mit | |||
<math>r = r_{i-1} + \ell_i\,\xi_i \text { und } r_{i-1} = (i-1)\cdot\ell_i</math> | |||
schreiben die Beziehung um zu | |||
<math>\displaystyle \delta W^a = \varrho\,A\,\Omega^2\,\ell_i^2 \cdot \int_{0}^{1} (i+\xi) \cdot \delta u(\xi)\;d\xi</math>, | |||
wir erhalten | |||
<math>\underline{P}_i = \varrho\,A\,\Omega^2\,\ell_i^2 \left(\begin{array}{c}\displaystyle \frac{3\,i+1}{6}\\\displaystyle \frac{3\,i+2}{6}\end{array}\right)</math>. {{MyCodeBlock|title=Declarations | |||
|text=Text | |text=Text | ||
|code= | |code= | ||
| Zeile 40: | Zeile 102: | ||
}} | }} | ||
==tmp== | ==tmp== | ||
<!-------------------------------------------------------------------------------->{{MyCodeBlock|title=Equlibrium Conditions | <!-------------------------------------------------------------------------------->Die Gleichgewichtsbeziehungen des Gesamtsystems erhalten wir durch aus der Addition aller virtuellen Arbeiten des Systems, praktisch durch das Hinzuaddieren der Anteile je Element in die System-Matrizen für ''K'' und ''P:'' | ||
<math>\underline{\underline{K}} = \begin{pmatrix}\frac{AE}{{{\ell}_{i}}} & -\frac{AE}{{{\ell}_{i}}} & 0 & 0 & 0\\ -\frac{AE}{{{\ell}_{i}}} & \frac{2AE}{{{\ell}_{i}}} & -\frac{AE}{{{\ell}_{i}}} & 0 & 0\\ 0 & -\frac{AE}{{{\ell}_{i}}} & \frac{2AE}{{{\ell}_{i}}} & -\frac{AE}{{{\ell}_{i}}} & 0\\ 0 & 0 & -\frac{AE}{{{\ell}_{i}}} & \frac{2AE}{{{\ell}_{i}}} & -\frac{AE}{{{\ell}_{i}}}\\ 0 & 0 & 0 & -\frac{AE}{{{\ell}_{i}}} & \frac{AE}{{{\ell}_{i}}}\end{pmatrix}</math> | |||
und | |||
<math>\underline{P} = \varrho\,A\,\ell_i^2\,\Omega^2 \cdot \begin{pmatrix}\frac{1}{6}\\ 1\\ 2\\ 3\\ \frac{11}{6}\end{pmatrix}</math>{{MyCodeBlock|title=Equlibrium Conditions | |||
|text=Text | |text=Text | ||
|code= | |code= | ||
| Zeile 48: | Zeile 116: | ||
}} | }} | ||
==tmp== | ==tmp== | ||
<!-------------------------------------------------------------------------------->{{MyCodeBlock|title=Boundary Conditions | <!-------------------------------------------------------------------------------->Die geometrische Randbedingung ''U<sub>0</sub> = 0'' arbeiten wir ein, indem wir die erste Zeile des Gleichungssystem streichen sowie die erste Spalte der Steifigketsmatrix.{{MyCodeBlock|title=Boundary Conditions | ||
|text=Text | |text=Text | ||
|code= | |code= | ||
| Zeile 56: | Zeile 124: | ||
}} | }} | ||
==tmp== | ==tmp== | ||
<!-------------------------------------------------------------------------------->{{MyCodeBlock|title=Solving | <!-------------------------------------------------------------------------------->Die Lösung des linearen Gleichungssystems | ||
<math>\underline{\underline{K}}\cdot \underline{U} = \underline{P}</math> | |||
ist | |||
<math>\underline{U} = \begin{pmatrix}\frac{47{{l}_{0}^{3}}\,{{\Omega}^{2}}\rho}{384E}\\ \frac{11{{l}_{0}^{3}}\,{{\Omega}^{2}}\rho}{48E}\\ \frac{39{{l}_{0}^{3}}\,{{\Omega}^{2}}\rho}{128E}\\ \frac{{{l}_{0}^{3}}\,{{\Omega}^{2}}\rho}{3E}\end{pmatrix}</math>. | |||
Oder - in dimensionsloser Form | |||
<math>\displaystyle \frac{\underline{U}}{u_s} = \begin{pmatrix}\frac{47}{128}\\ \frac{11}{16}\\ \frac{117}{128}\\ 1\end{pmatrix}</math>.{{MyCodeBlock|title=Solving | |||
|text=Text | |text=Text | ||
|code= | |code= | ||
| Zeile 65: | Zeile 143: | ||
==tmp== | ==tmp== | ||
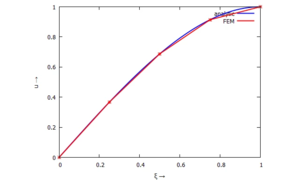
<!-------------------------------------------------------------------------------->[[Datei:FEB1-11.png|mini|Auslenkung ''u(x)''.]] | |||
Die Ergebnisse der FE-Rechnung und der analytischen Lösung können wir jetzt übereinander auftragen: | |||
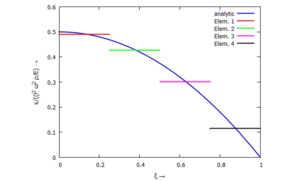
Die Dehnungen (und Spannungen) im Bauteil sind | |||
<math>\displaystyle \varepsilon_{rr} = \frac{du}{dr}</math>. | |||
Auch dieses Ergebnis können wir auftragen:[[Datei:FEB1-12.png|mini|Dehnung ε(x).|alternativtext=|links]]{{MyCodeBlock|title=Post-Processing | |||
|text= | |text= | ||
Version vom 25. Februar 2021, 13:30 Uhr
Aufgabenstellung
Auch wenn es nicht so aussieht: für das rotierende Rotorblatt suchen wir eine statische Lösung - das Problem heißt "quasistatisch".
Ein Hubschrauber-Rotor dreht mir der konstanten Winknelgeschwindigkeit Ω. Das Rotor-Blatt ist aus Aluminium. Gesucht ist die FEM-Lösung für der Verschiebung der Querschnitte und die Dehnung der Querschnitte.
Lösung mit Maxima
Lorem Ipsum ....
tmp
Zu diesem Problem finden wir einfach eine analytische Lösung - die nutzen wir später, um unsere Ergebnisse dimensionslos zu machen.
Ausgangspunkt ist die Gleichgewichtsbeziehung des Dehnstabes. Die Streckenlast n (hier n(r)) ist die Zentrifugalkraft - oder die D'Alembert'sche Trägheitskraft der Zentripetalbeschleunigung, also
.
Die Bewegungsgleichung lautet dann
.
Die allgemeine Lösung ist
,
angepasst an die Randbedingungen
erhalten wir
.
Als Bezugslänge gewinnen wir hier
===Header=== Text
1+1
tmp
Für die Komposition der Bewegungsgleichungen brauchen wir die Element-Steifigkeitsmatrix und die Element-Lastmatrix.
Wir gehen von gleichlangen Elementen aus, hier von
Elementen, also
.
Wie im Abschnitt "Finite Elemente Methode" verwenden wir die linearen Ansatzfunktionen
,
also
.
Die Element-Steifigkeitsmatrix ergibt sich für den Dehnstab zu
.
Die Element-Lastmatrix ist etwas schwieriger. Für ein einzelnes Element i ist
.
Mit
schreiben die Beziehung um zu
,
wir erhalten
. ===Declarations=== Text
1+1
tmp
Die Gleichgewichtsbeziehungen des Gesamtsystems erhalten wir durch aus der Addition aller virtuellen Arbeiten des Systems, praktisch durch das Hinzuaddieren der Anteile je Element in die System-Matrizen für K und P:
und
===Equlibrium Conditions=== Text
1+1
tmp
Die geometrische Randbedingung U0 = 0 arbeiten wir ein, indem wir die erste Zeile des Gleichungssystem streichen sowie die erste Spalte der Steifigketsmatrix.===Boundary Conditions=== Text
1+1
tmp
Die Lösung des linearen Gleichungssystems
ist
.
Oder - in dimensionsloser Form
.===Solving=== Text
1+1
tmp
Die Ergebnisse der FE-Rechnung und der analytischen Lösung können wir jetzt übereinander auftragen:
Die Dehnungen (und Spannungen) im Bauteil sind
.
Auch dieses Ergebnis können wir auftragen:
===Post-Processing===
| ✔ Konstante Dehnung je Element: |
| Was ausschaut wie ein Fehler - nämlich die "Treppenfunktion" für die Dehnung im FE-Modell - ist in Wirklichkeit die Folge unserer linearen Ansatzfunktionen. Diese abgeleitet liefern eine konstante Dehnung je Element. |
1+1
Links
- ...
Literature
- ...