Gelöste Aufgaben/FEAG: Unterschied zwischen den Versionen
| Zeile 213: | Zeile 213: | ||
===== Particular Solution ===== | ===== Particular Solution ===== | ||
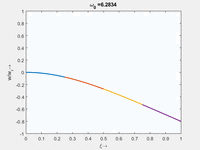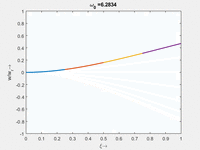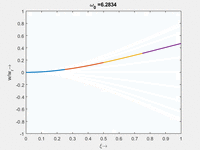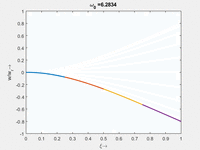
[[Datei:FEAG-12-particulareLösung.png|mini|Particulare Lösung.]] | |||
Die rechte Seite der Bewegungsgleichung ''G'' ist nicht zeitabhängig - sie ist statisch. Also ist auch die Lösung ''Q<sub>p</sub>'' statisch, wir suchen nach der Lösung des Gleichungssystems | Die rechte Seite der Bewegungsgleichung ''G'' ist nicht zeitabhängig - sie ist statisch. Also ist auch die Lösung ''Q<sub>p</sub>'' statisch, wir suchen nach der Lösung des Gleichungssystems | ||
<math>\underline{\underline{K}}\cdot\underline{Q}_p = \underline{G}</math> | :: <math>\underline{\underline{K}}\cdot\underline{Q}_p = \underline{G}</math> | ||
und die ist - mit der Normierung durch ''w<sub>s</sub>'' - | |||
<code> | <code> | ||
>> Qp | >> Qp | ||
Version vom 25. Februar 2021, 08:48 Uhr
Aufgabenstellung
Analog zu FEAF untersuchen wir hier die Schwingungen eines Kontinuums beim Loslassen aus der entspannten Rugelage. Hier nicht mit einem Dehnstab, sondern einem Euler-Bernoulli-Balken.
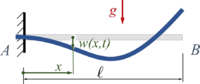
Gesucht ist die Schwingung eines Euler-Bernoulli-Balkens beim Loslassen aus der Ruhelage. Wir gehen nach dem Standardrezept der Finite Elemente Methode vor, arbeiten also mit dem Sources/Lexikon/Prinzip der virtuellen Arbeit.
Lösung mit Matlab
Interessant ist hier, dass - im Gegensatz zu Stablängsschwingungen - die Eigenfrequenz nicht ein gerades Vielfaches der untersten Eigenfrequenz ist. Falls Sie ein Saiteninstrument spielen, verstehen Sie sofort, warum das wichtig ist.
Maxima können wir hier nicht gut gebrauchen: die Gleichungen werden zu umfangreich. Wir arbeiten also mehr mit numerischen Verfahren, da ist Matlab geeigneter. Allerdings können wir Matlab-Inhalte nicht gut auf dieser Seite unterbringen - deshalb gibt es dafür die Seite FEAG-Matlab, die der gleichen Struktur folgt.
Header
Im Programm arbeiten wir mit einer dimensionslosen Formulierung - wir brauchen dafür eine Bezugszeit tBez und eine Bezugslänge lBez.
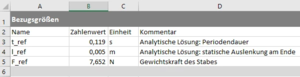
Bezugsgrößen wählen
Dazu nehmen wir eine "Anleihe" bei der analytischen Lösung des Schwingungsproblems (vgl. Aufgabe SKEB):
|
Analytische Lösung: homohener Lösungsanteil |
Analytische Lösung: partikularer Lösungsanteil |
|---|---|
|
Die homogene Bewegungsgleichung des Euler-Bernoulli-Balkens hat Lösungen vom Typ Wir bekommen zu jedem ω0 vier κ Das α ist eine praktische Abkürzung, hinter der wir ω0 verstecken. Anders als beim Dehnstab (SKER) finden wir hier keine analytische Beziehung, sondern nur die numerischen Beziehungen, für die unsere Randbedingungen erfüllt sind: Die langsamste Eigenmode gehört zu α1 mit der Periodendauer
Also wählen wir . |
Die zugeordnete inhomogene Bewegungsgleichung des Euler-Bernoulli-Balkens hat die partikulare Lösung Die statische Auslenkung am unteren Ende ist demnach
Wir wählen \ell_{Bez} := w_s. |
System-Parameter des FEM-Modells
Für die Diskretisierung wählen wir als Anzahl der Finiten Elemente (Number Of Elements):
und damit je Element
.
Wir wählen die kubische Ansatzfunktionen aus dem Abschnitt Finite Elemente Methode je Element, also
Für die numerisch Implementierung stört in dieser Darstellung das Element-spezifische ℓi - die Elementlänge. Wir behelfen uns, indem wir die Ansatzfunktionen schreiben als
,
wobei wir die Ansatz-Polynome in verpacken.
Das schaut unnötig komplex aus - allerdings stecken wir die Diagonal-Matrizen d (für jedes Element eine) in eine Matlab-Variable, so dass sie dort nicht weiter auffällt.
Die abhängigen Koordinaten des FEM-Modells sind dann zunächst - bis zum Einarbeiten der Randbedingungen - diese:
.
Equilibrium Conditions
xffsd
Die Gleichgewichtsbedingung mit dem Prinzip der virtuellen Verrückungen setzen sich additiv aus
,
zusammen - also den virtuellen Arbeiten je Element zuzüglich von virtuellen Arbeiten am Rand. In unserem Beispiel haben wir allerdings keine eingeprägten, äußeren Lasten am Rand, also ist
.
Je Element erfassen wir die virtuellen Arbeiten durch Element-Matrizen. So ist z.B. für die virtuelle Formänderungsenergie (vgl. Finite Elemente Methode)
mit der Element-Steifigkeitsmatrix .
Aus der FEM-Formulierung für den Euler-Bernoulli-Balken könnten wir die Element-Matrizen der virtuellen Arbeit der D'Alembert'schen Trägheitskraft sowie der Virtuelle Formänderungsenergie herauskopieren. Auch die "rechte Seite" mit der virtuelle Arbeit der Gewichtskraft aus
,
könnten wir als Element-Lastmatrix (Spaltenmatrix) abspeichern.
.
Dass es auch anders geht,sehen Sie in der Definition der Matlab-Klasse FEM_Element_Modell, bei der die Element direkt aus den Trial-Functions - hier den
-
hergeleitet. werden:
:
K(row,col) = diff(...
polyval(...
polyint(...
conv(polyder(self.phi(row,:)),polyder(self.phi(col,:)))),...
[0,1]));
:
|
Komponieren der System-Matrizen
Die System-Matrizen des Gesamt–Systems komponieren wir nun durch Hinzuaddieren der Anteile je Element.
Beispiel: die Gesamt-Steifigkeitsmatrix für I=2:
Die Beiträge der zwei Elemente sind hier in rot bzw. grün eingefärbt.
Dieses "Hinzuaddieren" passiert in Matlab hier:
:
e = 0;% counter for all elements of all sections
for section = 1: length(element.noe)
:
for i = 1:element.noe(section)
e = e+1;
:
j = 2*(e-1)+1;
:
K(j:j+3,j:j+3) = K(j:j+3,j:j+3)+b* d(:,:,e)*element.K*d(:,:,e);
:
end
:
|
In Matrix-Schreibweise lautet die Bewegungsgleichung des Gesamt-Systems jetzt:
.
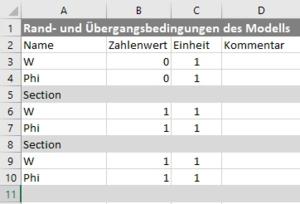
Einarbeiten der Randbedingungen
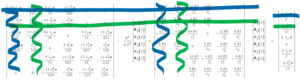
Die Randbedingungen arbeiten wir ein, indem wir zeilenweise (für δW und δΦ) und spaltenweise (für W und Φ) streichen.
Hier sind es
- die erste Zeile/Spalte für W0 (blau) und
- die zweite Zeile / Spalte für Φ0 (grün).
Die Lösung des Anfangs- und Randwertproblems ist in diesem Lösungsansatz mit Matlab um die Klasse "FEM_Container" herum aufgebaut - in ihr sind alle Parameter und Lösungsprozesse beschrieben.
Hier heißt die Instanz des Modells
- mathModel
In diesem Container sind alle Parameter und Zustandsgrößen des Modells bereits dimensionslos gemacht - und zwar mit den oben genannten Bezugsgrößen, die in der Excel-Eingabedatei im Blatt "0) Bezugsgrößen" definiert sind.
Die Lösung des Anfangswertproblems setzt sich aus zwei Teilen zusammen:
- der partikularen Lösung, die die Rechte Seite "G" erfüllt und
- der homogenen Lösung, die die Rechte Seite "0" erfüllt.
Die Gesamtlösung Qt setzt sich nun - bei diesem linearen System - additiv aus partikularer Qp und Qh homogener Lösung zusammen:
Particular Solution
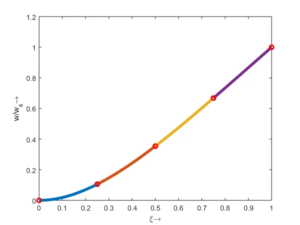
Die rechte Seite der Bewegungsgleichung G ist nicht zeitabhängig - sie ist statisch. Also ist auch die Lösung Qp statisch, wir suchen nach der Lösung des Gleichungssystems
und die ist - mit der Normierung durch ws -
>> Qp
Qp =
0
0
0.1055
0.0042
0.3542
0.0064
0.6680
0.0072
1.0000
0.0073
Diese Lösung tragen wir - elementweise - auf.
Homogene Lösung
Zur Lösung der homogenen Bewegungsgleichung
setzen wir an
und erhalten das Eigenwertproblem
mit
| den Eigenwerten | und |
| den Egenvektoren | . |
Für die Berechnung der Eigenwerte λ müssen wir die Abkürzung
einführen. Damit arbeitet die Matlab-Routine "eig()", die in "mathModel.eigensystem()" implementiert ist.
Acht Eigenwerte kommen aus der Bedingung , diese werden auf der Spur der Matrix D abgelegt:
>> D
D =
1.0e+06 *
-2.9006 0 0 0 0 0 0 0
0 -1.0774 0 0 0 0 0 0
0 0 -0.4287 0 0 0 0 0
0 0 0 -0.1662 0 0 0 0
0 0 0 0 -0.0480 0 0 0
0 0 0 0 0 -0.0123 0 0
0 0 0 0 0 0 -0.0016 0
0 0 0 0 0 0 0 -0.0000
Die zugehörigen dimensionslosen Periodendauern sind
.
Und offensichtlich fällt die längste Periodendauer T8 mit der analytisch berechneten untersten Schwingunsperiode T* zusammen.
Die zugehörigen Eigenvektoren stehen in V:
>> V
V =
-0.0579 0.2951 -0.0687 0.3043 0.4561 0.5309 -0.3197 -0.0780
-0.0129 0.0882 -0.0805 -0.0578 -0.0115 0.0064 -0.0096 -0.0032
-0.0884 -0.1020 0.4873 -0.0417 -0.4707 0.0160 -0.5469 -0.2721
-0.0364 0.1230 0.0134 0.0659 -0.0007 -0.0222 0.0019 -0.0051
-0.1652 -0.4100 -0.2420 -0.1979 0.4058 -0.4268 -0.1035 -0.5270
-0.0763 0.0330 0.0704 -0.0601 0.0098 0.0106 0.0163 -0.0059
-0.9540 -0.8313 -0.8232 0.9212 -0.6357 0.7308 0.7663 -0.8013
-0.2099 -0.1390 -0.0999 0.0809 -0.0389 0.0315 0.0200 -0.0060
Die Eigenvektoren in V spannen nun den Nullraum (nullspace) der Matrix auf, es ist
Die homogene Lösung der Bewegungsgleichung lautet damit
mit den acht Integrationskonstanten Ci . Durch die komplexen Eigenwerte sind die Integrationskonstanten nun (eigentlich) auch komplexwertig. Darum kommen in diesem Fall herum, weil die Anfangsgeschwindigkeit des Balkens beim Loslassen Null ist - wir also nur cos-Anteile berücksichtigen müssen. Und die gehören wiederum zum Realteil der Exponential-Funktion.
Die Ci sind nun die Konstanten, die wir brauchen, um die Lösung an Anfangsbedingungen anzupassen.
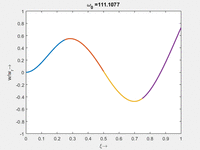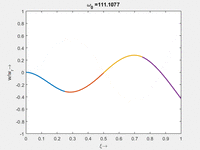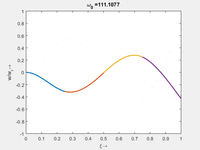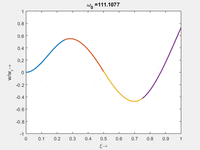
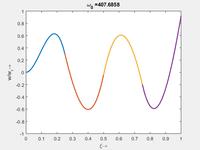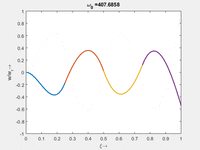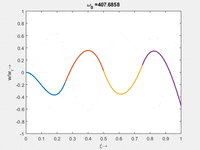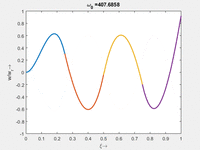
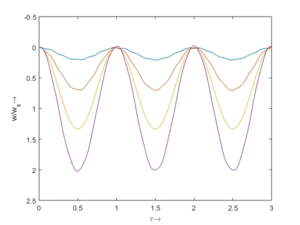
Vorher schauen wir uns die Lösung jeweils zu einer Eigenfrequenz ωi an. Diese Funktionen heißen Modalformen ϕ(x) und deren Schwingungen können wir plotten:
| Mode | Modalform ϕj(x) | Mode | Modalform ϕj(x) |
|---|---|---|---|
| #8<br/ | |||
| Mode | Modalform ϕj | Mode | Modalform ϕj |
|---|---|---|---|
| #7
|
|||
| #6
|
#5
|
||
| #4
|
#3
|
| ✔ Zur Euler-Bernoulli-Hypothese: |
| Praktisch haben die höheren Moden kaum Relevanz - meist klingen sie durch Dämpfung schnell ab. Man sieht allerdings bereits an der Schwingungs-Form, dass hier die Länge zwischen zwei Knoten nicht mehr sehr klein ist im Vergleich zur Höhe. Und das führt dazu, dass Schubverformungen eine Rolle spielen. Wir müssen zum Timoshenko-Balken wechseln .... |
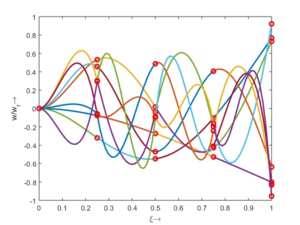
Alle acht Moden ϕj können wir auch zum Zeitpunkt τ=0 übereinander darstellen:
Solving
xffsd
Adapt to Initial Conditions
xffsd
Post-Processing
xffsd
Header
xffsd
Header
xffsd
Links
- ...
Literature
- ...
 |
 |
 |
| ||
| ||
|