Gelöste Aufgaben/FEAG: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 25: | Zeile 25: | ||
[[Werkzeuge/Software/Maxima|Maxima]] können wir hier nicht gut gebrauchen: die Gleichungen werden zu umfangreich. Wir arbeiten also mehr mit numerischen Verfahren, da ist [[Werkzeuge/Software/Matlab|Matlab]] geeigneter. Allerdings können wir Matlab-Inhalte nicht gut auf dieser Seite unterbringen - deshalb gibt es dafür die Seite [[Gelöste Aufgaben/FEAG/FEAG-Matlab|FEAG-Matlab]], die der gleichen Struktur folgt. | [[Werkzeuge/Software/Maxima|Maxima]] können wir hier nicht gut gebrauchen: die Gleichungen werden zu umfangreich. Wir arbeiten also mehr mit numerischen Verfahren, da ist [[Werkzeuge/Software/Matlab|Matlab]] geeigneter. Allerdings können wir Matlab-Inhalte nicht gut auf dieser Seite unterbringen - deshalb gibt es dafür die Seite [[Gelöste Aufgaben/FEAG/FEAG-Matlab|FEAG-Matlab]], die der gleichen Struktur folgt. | ||
<!-------------------------------------------------------------------------------->Im Programm arbeiten wir mit einer dimensionslosen Formulierung - wir brauchen dafür eine Bezugszeit ''t<sub>Bez</sub>'' und eine Bezugslänge ''l<sub>Bez</sub>''. | <!-------------------------------------------------------------------------------->{MyNoncodeBlock|title=Header | ||
|text= | |||
Im Programm arbeiten wir mit einer dimensionslosen Formulierung - wir brauchen dafür eine Bezugszeit ''t<sub>Bez</sub>'' und eine Bezugslänge ''l<sub>Bez</sub>''. | |||
Dazu nehmen wir eine "Anleihe" bei der analytischen Lösung des Schwingungsproblems (vgl. Aufgabe [[Gelöste Aufgaben/SKEB|SKEB]]): | Dazu nehmen wir eine "Anleihe" bei der analytischen Lösung des Schwingungsproblems (vgl. Aufgabe [[Gelöste Aufgaben/SKEB|SKEB]]): | ||
Version vom 25. Februar 2021, 07:22 Uhr
Aufgabenstellung
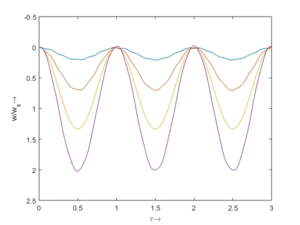
Analog zu FEAF untersuchen wir hier die Schwingungen eines Kontinuums beim Loslassen aus der entspannten Rugelage. Hier nicht mit einem Dehnstab, sondern einem Euler-Bernoulli-Balken.
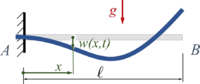
Gesucht ist die Schwingung eines Euler-Bernoulli-Balkens beim Loslassen aus der Ruhelage. Wir gehen nach dem Standardrezept der Finite Elemente Methode vor, arbeiten also mit dem Sources/Lexikon/Prinzip der virtuellen Arbeit.
Lösung mit Matlab
Interessant ist hier, dass - im Gegensatz zu Stablängsschwingungen - die Eigenfrequenz nicht ein gerades Vielfaches der untersten Eigenfrequenz ist. Falls Sie ein Saiteninstrument spielen, verstehen Sie sofort, warum das wichtig ist.
Maxima können wir hier nicht gut gebrauchen: die Gleichungen werden zu umfangreich. Wir arbeiten also mehr mit numerischen Verfahren, da ist Matlab geeigneter. Allerdings können wir Matlab-Inhalte nicht gut auf dieser Seite unterbringen - deshalb gibt es dafür die Seite FEAG-Matlab, die der gleichen Struktur folgt.
{MyNoncodeBlock|title=Header |text= Im Programm arbeiten wir mit einer dimensionslosen Formulierung - wir brauchen dafür eine Bezugszeit tBez und eine Bezugslänge lBez.
Dazu nehmen wir eine "Anleihe" bei der analytischen Lösung des Schwingungsproblems (vgl. Aufgabe SKEB):
|
Analytische Lösung: homohener Lösungsanteil |
Analytische Lösung: partikularer Lösungsanteil |
|---|---|
|
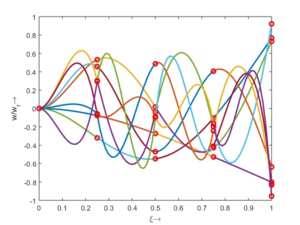
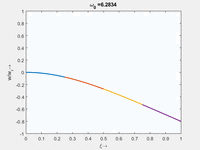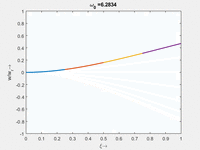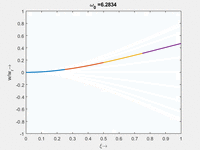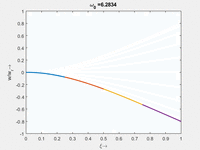
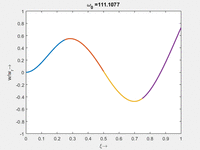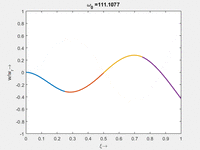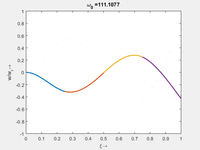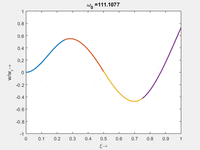
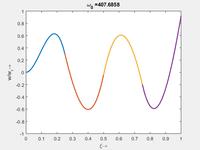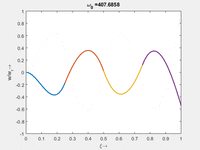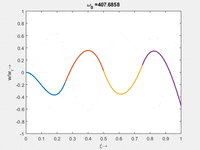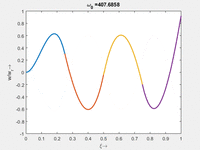
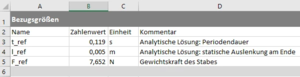
Die homogene Bewegungsgleichung des Euler-Bernoulli-Balkens hat Lösungen vom Typ Wir bekommen zu jedem ω0 vier κ Das α ist eine praktische Abkürzung, hinter der wir ω0 verstecken. Anders als beim Dehnstab (SKER) finden wir hier keine analytische Beziehung, sondern nur die numerischen Beziehungen, für die unsere Randbedingungen erfüllt sind: Die langsamste Eigenmode gehört zu α1 mit der Periodendauer
Also wählen wir . |
Die zugeordnete inhomogene Bewegungsgleichung des Euler-Bernoulli-Balkens hat die partikulare Lösung Die statische Auslenkung am unteren Ende ist demnach
Wir wählen \ell_{Bez} := w_s. |
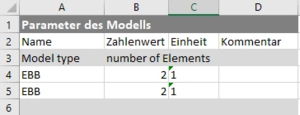
System-Parameter des FEM-Modells
Für die Diskretisierung wählen wir als Anzahl der Finiten Elemente (Number Of Elements):
und damit je Element
.
Wir wählen die kubische Ansatzfunktionen aus dem Abschnitt Finite Elemente Methode je Element, also
Für die numerisch Implementierung stört in dieser Darstellung das Element-spezifische li - die Elementlänge. Wir behelfen uns, indem wir die Ansatzfunktionen schreiben als
,
wobei wir die Ansatz-Polynome in verpacken.
Das schaut unnötig komplex aus - allerdings stecken wir die Diagonal-Matrizen d (für jedes Element eine) in eine Matlab-Variable, so dass sie dort nicht weiter auffällt.
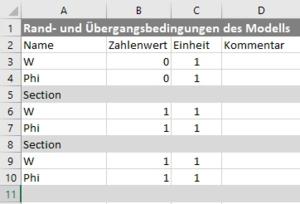
Die abhängigen Koordinaten des FEM-Modells sind dann zunächst - bis zum Einarbeiten der Randbedingungen - diese:
.
Header
xffsd
Equilibrium Conditions
xffsd
Solving
xffsd
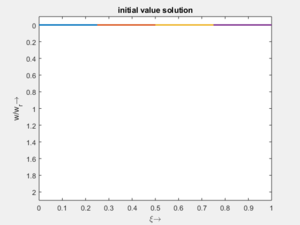
Adapt to Initial Conditions
xffsd
Post-Processing
xffsd
Header
xffsd
Header
xffsd
Links
- ...
Literature
- ...
 |
 |
 |
| ||
| ||
|