Gelöste Aufgaben/DGEC: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
|||
| Zeile 26: | Zeile 26: | ||
<!--------------------------------------------------------------------------------> | <!--------------------------------------------------------------------------------> | ||
==tmp== | ==tmp== | ||
{{MyCodeBlock|title=Header | Wir suchen Näherungslösungen für die Verschiebung des Punktes ''B'' mit dem Prinzip der virtuellen Verrückungen auf Basis der Bewegungsgleichungen aus DGEB. Dazu setzen wir einmal die Verschiebung und Verdrehung der Querschnitte jeweils nach dem Modell des | ||
* Timoshenko-Balkens und | |||
* Euler-Bernoulli-Balkens | |||
an.{{MyCodeBlock|title=Header | |||
|text=Text | |text=Text | ||
|code= | |code= | ||
| Zeile 35: | Zeile 40: | ||
<!--------------------------------------------------------------------------------> | <!--------------------------------------------------------------------------------> | ||
==tmp== | ==tmp== | ||
<math>\displaystyle G=\frac{E}{2 \left( \nu+1\right) },\nu=\frac{3}{10},A={{h}^{2}},I=\frac{{{h}^{4}}}{12}</math> | |||
{{MyCodeBlock|title=Parameter | {{MyCodeBlock|title=Parameter | ||
|text= | |text=Parameter sind | ||
<math></math> | |||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
| Zeile 44: | Zeile 52: | ||
<!--------------------------------------------------------------------------------> | <!--------------------------------------------------------------------------------> | ||
==tmp== | ==tmp== | ||
{{MyCodeBlock|title=Trial-Functions | Wir wählen als Trial-Functions für die Auslenkung ''w'' und die Verdrehung ''ϕ'' des Timoshenko-Balkens: | ||
<math>\begin{array}{ll}w(x) &= W \cdot (3\,\xi^2-2\,\xi^3),\\ \phi(x) &= \Phi\cdot 4\,\xi\,(1-\xi) \end{array}</math> . | |||
Beim Euler-Bernoulli-Balken ist | |||
<math>\phi(x) = w')(x)</math> | |||
fest "eingebaut" - wir brauchen keine Trial-Funktion für ''ϕ''. | |||
Und so sehen die beiden Trial-Funtions aus:{{MyCodeBlock|title=Trial-Functions | |||
|text=Text | |text=Text | ||
|code= | |code= | ||
| Zeile 53: | Zeile 71: | ||
<!--------------------------------------------------------------------------------> | <!--------------------------------------------------------------------------------> | ||
==tmp== | ==tmp== | ||
{{MyCodeBlock|title=Equilibrium-Conditions | Mit dem Prinzip der virtuellen Verrückungen lautet die Gleichgewichtsbedingung | ||
<math>\begin{array}{ll}\delta W &= \delta W^a - \delta \Pi\\&\stackrel{!}{=}0\end{array}</math>. | |||
Aus DGEB wissen wir für die Virtuelle Formänderungsenergie | |||
{| class="wikitable" | |||
!... für den Timoshenko-Balken | |||
!... für den Euler-Bernoulli-Balken | |||
|- | |||
|<math>\begin{array}{lcl} \delta\Pi = &\displaystyle \int_0^\ell& \displaystyle \frac{1}{4} G\,A\,(w'-\phi)\cdot (\delta w'-\delta \phi) \\&+ &E\,I\,\phi'\,\delta \phi' \; dx \end{array}</math> | |||
|<math>\displaystyle \delta\Pi = \int_0^\ell EI\,w''\,\delta w'' \; dx</math> | |||
|} | |||
Und die virtuelle Arbeit der äußeren Kraft ''F'' ist | |||
<math>\delta W^a = F\;\delta W</math>{{MyCodeBlock|title=Equilibrium-Conditions | |||
|text=Text | |text=Text | ||
|code= | |code= | ||
| Zeile 62: | Zeile 94: | ||
<!--------------------------------------------------------------------------------> | <!--------------------------------------------------------------------------------> | ||
==tmp== | ==tmp== | ||
Aus den Gleichgewichtsbedingungen erhalten wir die Gleichungen von | |||
* ''W'' und ''Φ'' für den Timoshenko-Balken und | |||
* ''W'' für den Euler-Bernoulli-Balken. | |||
{| class="wikitable" | |||
!Timoshenko | |||
!Euler-Bernoulli | |||
|- | |||
|<math>\begin{array}{ll}\displaystyle \frac{3 \, G A}{10 \, \ell} \cdot W-\frac{G A}{5} \cdot \Phi &=F,\\ | |||
\displaystyle \left(\frac{2\, G A\, \ell}{15}+\frac{16\, E I}{3 \ell}\right) \cdot \Phi -\frac{G A}{5}\cdot W&=0 | |||
\end{array}</math> | |||
|<math>\displaystyle \frac{12 \, E I}{{{\ell}^{3}}}\, W=F</math> | |||
|- | |||
| colspan="2" |mit der Lösung | |||
|- | |||
| colspan="1" |<math>\displaystyle W=\frac{G A\, {{\ell}^{3}}+40 \,E I\,\ell}{12\,E I\,G A}\,F,\;\;\Phi =\frac{{{\ell}^{2}}}{8\,E I}\,F</math> | |||
| colspan="1" |<math>\displaystyle W=\frac{{{\ell}^{3}}}{12\,E I}\,F</math> | |||
|} | |||
{{MyCodeBlock|title=Solving | {{MyCodeBlock|title=Solving | ||
|text=Text | |text=Text | ||
| Zeile 71: | Zeile 124: | ||
<!--------------------------------------------------------------------------------> | <!--------------------------------------------------------------------------------> | ||
==tmp== | ==tmp== | ||
{{MyCodeBlock|title=Post-Processing | Einsetzen der Parameter liefert die Verschiebung des Punkte | ||
<math>\displaystyle \tilde{W} = \frac{W}{\displaystyle \frac{\ell^3\,F}{E\,h^4}} \text{ für } \alpha = \frac{h}{\ell}:</math>: | |||
Wir sehen: für schlanke Balken bis α<0.2 können wir getrost mit der Euler-Bernoulli-Hypothese arbeiten - für "stäbigere" Balken brauchen wir mindestens das Timoshenko-Modell.{{MyCodeBlock|title=Post-Processing | |||
|text=Text | |text=Text | ||
|code= | |code= | ||
Version vom 23. Februar 2021, 11:56 Uhr
Aufgabenstellung
Wie sich die Balkenmodell von Euler-Bernoulli und Timoshenko in Ihrem Modellverhalten unterscheiden, untersuchen wir hier.
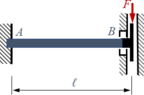
Ein Balken AB (Länge ℓ, Rechteck-Querschnitt h*b, Elastizitäts-Module E) ist in A fest eingespannt und in B durch eine Parallelführung gelagert.
In B wird er durch eine senkrechte Kraft F belastet.
Wir vergleichen die Auslenkung in B nach den Balken-Modellen von
Der Balken-Querschnitt sei rechteckig mit den Abmessungen h, b:
Hier gelte für den Querschnitt h=b.
Lösung mit Maxima
Lorem Ipsum ....
tmp
Wir suchen Näherungslösungen für die Verschiebung des Punktes B mit dem Prinzip der virtuellen Verrückungen auf Basis der Bewegungsgleichungen aus DGEB. Dazu setzen wir einmal die Verschiebung und Verdrehung der Querschnitte jeweils nach dem Modell des
- Timoshenko-Balkens und
- Euler-Bernoulli-Balkens
an.===Header=== Text
1+1
tmp
Parameter
Parameter sind
1+1
tmp
Wir wählen als Trial-Functions für die Auslenkung w und die Verdrehung ϕ des Timoshenko-Balkens:
.
Beim Euler-Bernoulli-Balken ist
fest "eingebaut" - wir brauchen keine Trial-Funktion für ϕ.
Und so sehen die beiden Trial-Funtions aus:===Trial-Functions=== Text
1+1
tmp
Mit dem Prinzip der virtuellen Verrückungen lautet die Gleichgewichtsbedingung
.
Aus DGEB wissen wir für die Virtuelle Formänderungsenergie
| ... für den Timoshenko-Balken | ... für den Euler-Bernoulli-Balken |
|---|---|
Und die virtuelle Arbeit der äußeren Kraft F ist
===Equilibrium-Conditions=== Text
1+1
tmp
Aus den Gleichgewichtsbedingungen erhalten wir die Gleichungen von
- W und Φ für den Timoshenko-Balken und
- W für den Euler-Bernoulli-Balken.
| Timoshenko | Euler-Bernoulli |
|---|---|
| mit der Lösung | |
Solving
Text
1+1
tmp
Einsetzen der Parameter liefert die Verschiebung des Punkte
:
Wir sehen: für schlanke Balken bis α<0.2 können wir getrost mit der Euler-Bernoulli-Hypothese arbeiten - für "stäbigere" Balken brauchen wir mindestens das Timoshenko-Modell.===Post-Processing=== Text
1+1
Links
- ...
Literature
- ...