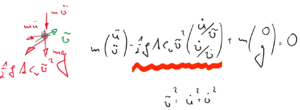Werkzeuge/Lösungsverfahren für Bewegungsgleichungen: Unterschied zwischen den Versionen
KKeine Bearbeitungszusammenfassung |
|||
| (16 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 2: | Zeile 2: | ||
Bewegungsgleichungen sind Differentialgleichungen für physikalische Systeme. Sie sind in der Technischen Mechanik meist Gleichgewichtsbeziehungen zwischen abhängigen Variablen, bei denen auch Ableitungen dieser Variablen vorkommen. | Bewegungsgleichungen sind Differentialgleichungen für physikalische Systeme. Sie sind in der Technischen Mechanik meist Gleichgewichtsbeziehungen zwischen abhängigen Variablen, bei denen auch Ableitungen dieser Variablen vorkommen. | ||
Für einen Euler-Bernoulli-Balken ist die gesuchte Variable z.B. der Verlauf des Schnittmoments ''M(x)'' in der Statik starrer Körper oder der Auslenkung ''w(x)'' in der Elastizitätstheorie. Die Bewegungsgleichungen lauten dann in ''x'' für | Für einen [[Sources/Lexikon/Euler-Bernoulli-Balken|Euler-Bernoulli-Balken]] ist die gesuchte Variable z.B. der Verlauf des [[Sources/Lexikon/Schnittmoment|Schnittmoments]] ''M(x)'' in der Statik starrer Körper oder der Auslenkung ''w(x)'' in der [[Sources/Lexikon/Elastizitätstheorie|Elastizitätstheorie]]. Die Bewegungsgleichungen lauten dann in ''x'' für | ||
* <math>M(x): M''(x) = -q(x)</math> | * <math>M(x): M''(x) = -q(x)</math> | ||
| Zeile 11: | Zeile 11: | ||
* die Lösung der "Bewegung" im Gebiet, also die Lösung einer Differentialgleichung und | * die Lösung der "Bewegung" im Gebiet, also die Lösung einer Differentialgleichung und | ||
* die algebraischen Bedingungen für die Bewegung an einem oder mehreren Rändern: | * die algebraischen Bedingungen für die Bewegung an einem oder mehreren Rändern: | ||
[[Datei:Lösungsverfahren-IVP-BVP.png|left|200px]]<br clear="all"/> | |||
So kann der Balken am linken Rand gelenkig gelagert sein - hier gilt also ''M=0''. | So kann der Balken am linken Rand gelenkig gelagert sein - hier gilt also ''M=0''. | ||
| Zeile 18: | Zeile 20: | ||
Wir unterscheiden zwischen Randwert- und Anfangswertproblemen. | Wir unterscheiden zwischen Randwert- und Anfangswertproblemen. | ||
Randwertprobleme geben Bedingungen für die gesuchten abhängigen Variablen an den Rändern des Gebiets vor. Bei Stäben heißt das: an "beiden" Seiten des Gebiets (two-point-boundary value problem). | Randwertprobleme geben Bedingungen für die gesuchten abhängigen Variablen an den Rändern des Gebiets vor. Bei [[Sources/Lexikon/Stab|Stäben]] heißt das: an "beiden" Seiten des Gebiets (two-point-boundary value problem). | ||
Anfangswertprobleme geben nur an einem Rand - am Anfang - Bedingungen für die gesuchten abhängigen Variablen vor. | Anfangswertprobleme geben nur an einem Rand - am Anfang - Bedingungen für die gesuchten abhängigen Variablen vor. | ||
| Zeile 24: | Zeile 26: | ||
Alle Probleme der Strukturmechanik sind Randwertprobleme. Viele Probleme der nichtlinearen Dynamik werden als Anfangswertprobleme gelöst. Und bei Schwingungen von Kontinua sind Randwertproblem und Anfangswertproblem gemischt. | Alle Probleme der Strukturmechanik sind Randwertprobleme. Viele Probleme der nichtlinearen Dynamik werden als Anfangswertprobleme gelöst. Und bei Schwingungen von Kontinua sind Randwertproblem und Anfangswertproblem gemischt. | ||
Alle Gleichgewichtsbedingungen der Stukturmechanik für Kontinua sind über Differentialgleichungen formuliert. Für uns Ingenieure sind sie deshalb die zentralen Bausteine für die Modellbildung und Simulation. Dabei sind praktisch alle relevanten Bewegungsgleichungen der Stukturmechanik Modelle, denen zum Teil gravierende Vereinfachungen zu Grunde liegen. So gelten die Bewegungsgleichungen für den Euler-Bernoulli-Balken oben nur, wenn | Alle Gleichgewichtsbedingungen der Stukturmechanik für Kontinua sind über Differentialgleichungen formuliert. Für uns Ingenieure sind sie deshalb die zentralen Bausteine für die Modellbildung und Simulation. Dabei sind praktisch alle relevanten Bewegungsgleichungen der Stukturmechanik Modelle, denen zum Teil gravierende Vereinfachungen zu Grunde liegen. So gelten die Bewegungsgleichungen für den [[Sources/Lexikon/Euler-Bernoulli-Balken|Euler-Bernoulli-Balken]] oben nur, wenn | ||
* der Balken in seiner unausgelenkten Lage gerade ist, | * der Balken in seiner unausgelenkten Lage gerade ist, | ||
| Zeile 33: | Zeile 35: | ||
Bei der Lösung von Differentialgleichungen lösen wir also bestimmte Modelle von Bewegungsgleichungen von Strukturen. Dabei beschreibt eine Bewegungsgleichung die Änderung der Variablen in den unabhängigen Variablen. So liest man die zwei Gleichgewichtsbedingungen | Bei der Lösung von Differentialgleichungen lösen wir also bestimmte Modelle von Bewegungsgleichungen von Strukturen. Dabei beschreibt eine Bewegungsgleichung die Änderung der Variablen in den unabhängigen Variablen. So liest man die zwei Gleichgewichtsbedingungen | ||
::<math>M'(x)=Q(x) \text{ und } Q'(x)=-q(x)</math> | |||
so: | so: | ||
* Die Änderung des Schnittmoments ''M(x)'' entlang der Koordinate ''x'' ist gleich der Querkraft im Balken. | * Die Änderung des Schnittmoments ''M(x)'' entlang der Koordinate ''x'' ist gleich der [[Sources/Lexikon/Querkraftverlauf|Querkraft]] im Balken. | ||
* Die Änderung der Querkraft ''Q(x)'' entlang der Koordinate ''x'' ist gleich der negativen äußeren Streckenlast im Balken. | * Die Änderung der Querkraft ''Q(x)'' entlang der Koordinate ''x'' ist gleich der negativen äußeren [[Sources/Lexikon/Streckenlast|Streckenlast]] im Balken. | ||
Für eine Reihe von einfachen Bewegungsgleichungen von eindimensionalen Kontinua (Euler-Bernoulli-Balken, Dehnstab, Torsionsstab) finden wir analytische Lösungen. Das sind die absoluten Ausnahmen. In der Regel muss man mit numerischen Näherungsverfahen arbeiten. | Für eine Reihe von einfachen Bewegungsgleichungen von eindimensionalen Kontinua ([[Sources/Lexikon/Euler-Bernoulli-Balken|Euler-Bernoulli-Balken]], [[Sources/Lexikon/Dehnstab|Dehnstab]], [[Sources/Lexikon/Torsionsstab|Torsionsstab]]) finden wir analytische Lösungen. Das sind die absoluten Ausnahmen. In der Regel muss man mit numerischen Näherungsverfahen arbeiten. | ||
| Zeile 46: | Zeile 50: | ||
{| class="wikitable" | {| class="wikitable" | ||
|+ | |+ | ||
!Randwertprobleme | !style="width:50%"|Randwertprobleme | ||
!Anfangswertprobleme | !Anfangswertprobleme | ||
|- | |- | ||
| | | | ||
[[Datei:Lösungsverfahren-BVP-1.png|left|mini|... im Zeitbereich: Flugbahn eines Körpers.]]<br clear="all"/> | |||
Lösungstypen: | Lösungstypen: | ||
| Zeile 57: | Zeile 61: | ||
* numerisch: mit dem Schiessverfahren | * numerisch: mit dem Schiessverfahren | ||
| | | | ||
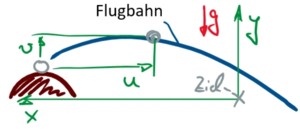
[[Datei:Lösungsverfahren-IVP-Flugbahn.png|left|mini|... im Zeitbereich: Flugbahn eines Körpers.]]<br clear="all"/> | |||
Lösungstypen: | Lösungstypen: | ||
| Zeile 65: | Zeile 69: | ||
|- | |- | ||
| | | | ||
[[Datei:Lösungsverfahren-BVP-Durchbiegung.png|left|mini|... im Raum: Durchbiegung eines Balkens]]<br clear="all"/> | |||
Lösungstypen: | Lösungstypen: | ||
* analytisch: Integration in ''x'' und Anpassung der Integrationskonstanten an die Randbedingungen | * [[Randwertprobleme/Methoden zur Lösung von Randwertproblemen/Integration der Differentialbeziehung (EBB)|analytisch: Integration in ''x'' und Anpassung der Integrationskonstanten an die Randbedingungen]] | ||
* analytisch: durch e<sup>κx</sup>-Ansatz | * analytisch: durch e<sup>κx</sup>-Ansatz | ||
* Finite Differenzen Verfahren (EBB) | * [[Randwertprobleme/Methoden zur Lösung von Randwertproblemen/Finite Differenzen Verfahren (EBB)|Finite Differenzen Verfahren]] | ||
* Finite Elemente Methode | * [[Randwertprobleme/Methoden zur Lösung von Randwertproblemen/Finite Elemente Methode|Finite Elemente Methode]] | ||
* Schießverfahren | * [https://de.wikipedia.org/wiki/Schie%C3%9Fverfahren Schießverfahren] | ||
| | | | ||
... im Raum | ... im Raum | ||
| Zeile 82: | Zeile 84: | ||
Für Strukturen kenne ich keine praxisrelevanten Anwendungen für eine Lösung als Anfangswertproblem im Raum. | Für Strukturen kenne ich keine praxisrelevanten Anwendungen für eine Lösung als Anfangswertproblem im Raum. | ||
|} | |} | ||
Für einen typische Vertreter je von Randwertproblem und Anfangswertproblem finden Sie hier ein Beispiel: | Für einen typische Vertreter je von Randwertproblem und Anfangswertproblem finden Sie hier ein Beispiel: | ||
| Zeile 88: | Zeile 89: | ||
{| class="wikitable" | {| class="wikitable" | ||
|+ | |+ | ||
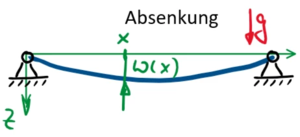
|Für den links und rechts gelenkig gelagerten Balken (Biegesteigifkeit ''EI'', Dichte ρ, Querschnittsfläche ''A'', Länge '' | |style="width:50%; vertical-align:top"|Für den links und rechts gelenkig gelagerten Balken (Biegesteigifkeit ''EI'', Dichte ρ, Querschnittsfläche ''A'', Länge ''ℓ'') ist | ||
<math>M''(x) = -q(x)</math> | ::<math>M''(x) = -q(x)</math> | ||
Die Bedingungen an den Rändern (''x=0'') und (''x= | Die Bedingungen an den Rändern (''x=0'') und (''x=ℓ'') sind | ||
::<math>M( 0 ) = 0</math> | |||
::<math>M(\ell) = 0</math> | |||
[[Datei:Lösungsverfahren-BVP.png|left]] | |||
|style="width:50%; vertical-align:top"| | |||
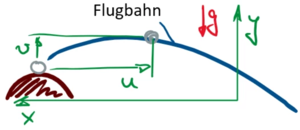
Für einen Golfball (Punktmasse) ist die Bewegungsgleichung in ''u(t)'' und ''v(t)'' | |||
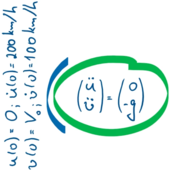
::<math>\left(\begin{array}{c}\ddot{u}(t)\\\ddot{v}(t)\end{array}\right) = \left(\begin{array}{c} 0\\ -g \end{array}\right)</math> | |||
Die Bedingungen zum Abschlagzeitpunkt(''t=0'') sind | |||
::<math>u(0) = 0 \text{ und } \dot{u}(0) = 200\text{km/h}</math> | |||
::<math>v(0) = 200\text{ cm} \text{ und } \dot{v}(0) = 180\text{ km/h}</math> | |||
[[Datei:Lösungsverfahren-IVP.png|170px|left]] | |||
|- | |- | ||
|Die Lösung mit Maxima liefert | |Die Lösung des BVP mit Maxima liefert | ||
|Die Lösung mit Maxima liefert | |Die Lösung des IVP mit Maxima liefert | ||
|- | |- | ||
|style="vertical-align:top" class="mw-collapsible mw-collapsed wikitable"| <syntaxhighlight lang=" | |style="vertical-align:top" class="mw-collapsible mw-collapsed wikitable" | <syntaxhighlight lang="lisp" line='line' style="border:1px solid blue"> | ||
/* Maxima */ | /* Maxima */ | ||
dgl: 'diff(M(x),x,2)+rho*A = 0; | dgl: 'diff(M(x),x,2)+rho*A = 0; | ||
| Zeile 113: | Zeile 128: | ||
[xlabel, "x/l →"], [ylabel, "M/(l^2*a*rho) →"]); | [xlabel, "x/l →"], [ylabel, "M/(l^2*a*rho) →"]); | ||
</syntaxhighlight> | </syntaxhighlight> | ||
|style="vertical-align:top" class="mw-collapsible mw-collapsed wikitable"| <syntaxhighlight lang=" | |style="vertical-align:top" class="mw-collapsible mw-collapsed wikitable"| <syntaxhighlight lang="lisp" line='line' style="border:1px solid blue"> | ||
/* Maxima */ | /* Maxima */ | ||
units: [cm=1/100*m, km = 1000*m, h=60*60*s]; | units: [cm=1/100*m, km = 1000*m, h=60*60*s]; | ||
| Zeile 136: | Zeile 151: | ||
</syntaxhighlight> | </syntaxhighlight> | ||
|- | |- | ||
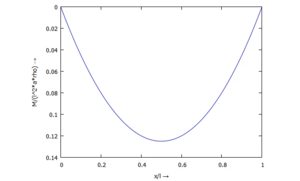
|den Schnittmomentenverlauf | |style="width:50%; vertical-align:top"|den Schnittmomentenverlauf | ||
::<math>\displaystyle M(x) =\frac{ | ::<math>\displaystyle M(x) =\frac{\ell^2 \cdot \rho\cdot A}{2} \cdot \xi \cdot \left(1 - \xi \right)</math>, | ||
mit seiner grafischen Auftragung: | mit seiner grafischen Auftragung: | ||
|den Verlauf der Koordinaten u, v | [[Datei:Lösungsverfahren-BVP-plot.png|left|mini|Schnittmomentenverlauf]]<br clear="all"/> | ||
|style="width:50%; vertical-align:top"|den Verlauf der Koordinaten u, v | |||
::<math>\begin{array}{cc} u\left( t\right) =&\displaystyle \frac{200\cdot \mathit{km}\cdot t}{h}\\\mathrm{v}\left( t\right) =&\displaystyle -\frac{g\cdot {{t}^{2}}}{2}+\frac{100\cdot \mathit{km}\cdot t}{h}+200\cdot \mathit{cm}\end{array}</math>, | ::<math>\begin{array}{cc} u\left( t\right) =&\displaystyle \frac{200\cdot \mathit{km}\cdot t}{h}\\\mathrm{v}\left( t\right) =&\displaystyle -\frac{g\cdot {{t}^{2}}}{2}+\frac{100\cdot \mathit{km}\cdot t}{h}+200\cdot \mathit{cm}\end{array}</math>, | ||
| Zeile 152: | Zeile 169: | ||
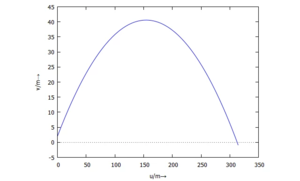
die grafische Auftragung in der Wurfparabel: | die grafische Auftragung in der Wurfparabel: | ||
[[Datei:Lösungsverfahren-IVP-plot.png|mini|Wurfparabel]]<br clear="all"/> | |||
Und das geht auch, wenn es keine analytische Lösung mehr gibt! | Und das geht auch, wenn es keine analytische Lösung mehr gibt! | ||
[[Datei:Lösungsverfahren-IVP-EOM.png|left|mini|Aufstellen der Bewegungsgleichungen]]<br clear="all"/> | |||
So kann man SEHR komplext Probleme lösen -z.B. Klimamodelle. | So kann man SEHR komplext Probleme lösen -z.B. Klimamodelle. | ||
|} | |} | ||
Aktuelle Version vom 19. Februar 2021, 14:20 Uhr
Bewegungsgleichungen sind Differentialgleichungen für physikalische Systeme. Sie sind in der Technischen Mechanik meist Gleichgewichtsbeziehungen zwischen abhängigen Variablen, bei denen auch Ableitungen dieser Variablen vorkommen.
Für einen Euler-Bernoulli-Balken ist die gesuchte Variable z.B. der Verlauf des Schnittmoments M(x) in der Statik starrer Körper oder der Auslenkung w(x) in der Elastizitätstheorie. Die Bewegungsgleichungen lauten dann in x für
Die Bewegungsgleichungen zu technischen System beschreiben die "Bewegung" (auch wenn es ein Problem der Statik ist) im Gebiet einer Struktur. Zur Lösung der Bewegungsgleichungen muss ich definieren, welchen Bedingungen die abhängigen Variablen am Rand des Gebiets unterliegen. Also gehören zu Aufgabenstellungen
- die Lösung der "Bewegung" im Gebiet, also die Lösung einer Differentialgleichung und
- die algebraischen Bedingungen für die Bewegung an einem oder mehreren Rändern:

So kann der Balken am linken Rand gelenkig gelagert sein - hier gilt also M=0.
Oder ein Golfball wird unter einer bestimmten Geschwindigkeit und Winkel vom Referenzpunkt abgeschlagen.
Wir unterscheiden zwischen Randwert- und Anfangswertproblemen.
Randwertprobleme geben Bedingungen für die gesuchten abhängigen Variablen an den Rändern des Gebiets vor. Bei Stäben heißt das: an "beiden" Seiten des Gebiets (two-point-boundary value problem).
Anfangswertprobleme geben nur an einem Rand - am Anfang - Bedingungen für die gesuchten abhängigen Variablen vor.
Alle Probleme der Strukturmechanik sind Randwertprobleme. Viele Probleme der nichtlinearen Dynamik werden als Anfangswertprobleme gelöst. Und bei Schwingungen von Kontinua sind Randwertproblem und Anfangswertproblem gemischt.
Alle Gleichgewichtsbedingungen der Stukturmechanik für Kontinua sind über Differentialgleichungen formuliert. Für uns Ingenieure sind sie deshalb die zentralen Bausteine für die Modellbildung und Simulation. Dabei sind praktisch alle relevanten Bewegungsgleichungen der Stukturmechanik Modelle, denen zum Teil gravierende Vereinfachungen zu Grunde liegen. So gelten die Bewegungsgleichungen für den Euler-Bernoulli-Balken oben nur, wenn
- der Balken in seiner unausgelenkten Lage gerade ist,
- Schubverformungen der Querschnitte klein sind,
- jeder Querschnitt eben bleibt und senkrecht zur Mittellinie,
- die Verschiebungen klein gegenüber der Balken-Länge sind und
- die Verzerrungen des Balkens im linearen Bereich bleiben.
Bei der Lösung von Differentialgleichungen lösen wir also bestimmte Modelle von Bewegungsgleichungen von Strukturen. Dabei beschreibt eine Bewegungsgleichung die Änderung der Variablen in den unabhängigen Variablen. So liest man die zwei Gleichgewichtsbedingungen
so:
- Die Änderung des Schnittmoments M(x) entlang der Koordinate x ist gleich der Querkraft im Balken.
- Die Änderung der Querkraft Q(x) entlang der Koordinate x ist gleich der negativen äußeren Streckenlast im Balken.
Für eine Reihe von einfachen Bewegungsgleichungen von eindimensionalen Kontinua (Euler-Bernoulli-Balken, Dehnstab, Torsionsstab) finden wir analytische Lösungen. Das sind die absoluten Ausnahmen. In der Regel muss man mit numerischen Näherungsverfahen arbeiten.
Randwert- und Anfangswertprobleme
Typische Randwert- und Anfangswertprobleme im Raum und in der Zeit sehen Sie hier tabelliert:
Für einen typische Vertreter je von Randwertproblem und Anfangswertproblem finden Sie hier ein Beispiel: