Werkzeuge/Gleichgewichtsbedingungen/Arbeitsprinzipe der Analytischen Mechanik/Prinzip vom Minimum der Potentiellen Energie: Unterschied zwischen den Versionen
Die Seite wurde neu angelegt: „m“ |
Keine Bearbeitungszusammenfassung |
||
| (8 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
=== Die Aussage === | |||
Die Aussage des Prinzips ist anschaulich: | |||
Von allen Zuständen, die ein System einnehmen kann, ist derjenige ein Gleichgewichtszustand, der die potentielle Energie des Systems minimiert. | |||
Also: | |||
::<math>\displaystyle U \stackrel{!}{=} \text{ Minimum,, also } \frac{d}{dq_i}U = 0 \text{ für alle abhängigen Koordinaten }q_i</math> | |||
Bei einfachen Systemen besteht ''U'' meist aus | |||
::<math>U = \Pi - A</math> | |||
mit dem [[Sources/Lexikon/Potential einer Kraft|Potential einer Kraft]] (''V=-A'') oder der [[Sources/Lexikon/Arbeitsfunktion|Arbeitsfunktion]] (''A)'' am System und der gespeicherten Energie der inneren Kräfte - der [[Sources/Lexikon/Formänderungsenergie|Formänderungsenergie]] ''Π''. | |||
Bei Aufgaben der Mechanik, bei denen Kräfte und Spannungen linear von den gesuchten Koordinaten abhängen, ist das Potential der Energie eines System immer eine quadratische Form: | |||
::<math>\displaystyle U(\underline{q}) = \frac{1}{2} \; \underline{q}^T\cdot \underline{\underline{A}}\cdot \underline{q} - \underline{q}^T \cdot \underline{b}</math> | |||
Für die Lösung nutzen wir unsere Überlegungen zu [[Sources/Lexikon/Minimum Prinzipe|Minimum Prinzipen]]. | |||
Hieraus kommt: ''U'' hat ein Minimum, wenn ''q'' | |||
::<math>\underline{\underline{A}}\cdot\underline{q} = \underline{b}</math> | |||
erfüllt. | |||
=== Beispiel: === | |||
[[Datei:ArbeitsprinzipeDerAnalytischenMechanik-Feder.png|left|150px|mini|Feder unter der Last ''F''.]] | |||
Eine Feder (Steifigkeit ''k'') wird durch die Kraft ''F'' belastet. | |||
Berechnen Sie die Federkompression ''u''. | |||
{{MyCodeBlock|title=Lösung mit Maxima|text=Die gesamte potentielle Enerfie des Systems ist die Formänderungsenergie Π minus dem Potential A der äußeren, eingeprägten Kraft F. | |||
::<math>\displaystyle U=\Pi-A \text{ mit } \Pi = \frac{1}{2} k \cdot u^2, A = F\cdot u</math> | |||
Einsetzen liefert | |||
::<math>U=\displaystyle \frac{k\cdot {{u}^{2}}}{2}-u\cdot F</math> | |||
und diese Funktion können wir plotten. | |||
[[Datei:PrinzipVomMinDerPotEn-Potential.png|mini|Potential ''U'' des Systems.]] | |||
Offensichtlich hat U ein Minimum bei u=10 mm und das muss auch aus der Gleichgewichtsbeziehung | |||
::<math>\displaystyle \frac{\partial U}{\partial u} = k\cdot u - F \stackrel{!}{=}0</math> | |||
herauskommen - und das tut es auch: | |||
::<math>u=F/k = 10 mm</math> | |||
|code=<syntaxhighlight lang="notmuch" line start=1> | |||
/* Maxima */ | |||
params: [k=10*N/mm, F=100*N]; | |||
PMPE : U = Pi-A; | |||
potEnergy : [A = F*u, Pi=1/2*k*(-u)^2]; | |||
/* potential energy */ | |||
PMPE : subst(potEnergy,PMPE); | |||
/* plot U */ | |||
plot2d(subst([u=upsilon*mm],subst(params,subst(PMPE,U/(N*mm)))), | |||
[upsilon,-5,25], | |||
[xlabel, "u/mm→"], [ylabel, "U/(N*mm)→"]); | |||
/* equilibrium condition */ | |||
equ : diff(subst(PMPE,U),u)=0; | |||
sol: solve(equ, u)[1] | |||
</syntaxhighlight>}} | |||
=== Anwendung für Kontinua === | |||
Die [[Sources/Lexikon/Formänderungsenergie|Formänderungsenergie]] für Kontinua besteht besonders bei [[Sources/Lexikon/Stab|Stab]]-Modellen aus einem charakteristischen quadratischen Term, den wir uns hier anhand des Euler-Bernoulli-Balkens anschauen. | |||
So setzten wir bei Näherungslösungen in den Ausdruck | |||
::<math>\displaystyle \Pi = \frac{1}{2} \int_\ell E\;I\; (w'')^2 \; dx</math> | |||
die Näherungslösung | |||
::<math>\tilde{w}(x) = \sum_i W_i\cdot \phi_i(x)</math> | |||
mit dem gesuchten Wichtungsfaktor Wi und den [[Sources/Lexikon/Trial-Function|Trial-Functions]] | |||
::<math>\phi_i(x)</math> | |||
Für das Näherungsverfahren, müssen diese Funktionen linear unabhängig voneinander sein und den geometrischen (oder essentiellen) [[Sources/Lexikon/Randbedingung|Randbedingungen]] genügen. | |||
Ansonsten dürfen es beliebig viele sein, wir erhalten also Gleichungssysteme für entsprechend viele Wi. | |||
Charakteristisch für das Verfahren vom Minimum der Potentiellen Energie - wie auch dem [[Werkzeuge/Gleichgewichtsbedingungen/Arbeitsprinzipe der Analytischen Mechanik/Prinzip der virtuellen Verrückungen|Prinzip der virtuellen Verrückungen]] - ist das Entstehen von Integralen mit Paaren von Integranden aus den Trial-Functions. So ist | |||
::<math>\boldsymbol{\Pi} \propto \displaystyle \frac{1}{2}\,\int_\ell (w'')^2 \; dx = \displaystyle \frac{1}{2}\, \int_\ell \left(\sum_i W_i \cdot \phi_i''(x)\right) \cdot \left(\sum_i W_i \cdot \phi_i''(x)\right) \; dx</math> | |||
Diesen Ausdruck können wir umschreiben als | |||
::<math>\boldsymbol{\Pi} \propto \displaystyle\frac{1}{2}\, \int_\ell (w'')^2 dx = \frac{1}{2}\, \underline{W}^T\cdot \underline{\underline{A}}\cdot \underline{W}</math> | |||
mit | |||
::<math>\displaystyle a_{i,j} = \int_\ell \phi_i''\cdot \phi_j'' \; dx</math>. | |||
Diesen Umstand nutzen wir beim Aufstellen der Bewegungsgleichungen mit dem Rechner (vgl. [[Werkzeuge/Software/Matlab#conv|conv→]] ) | |||
'''Links''' | |||
* [https://en.wikipedia.org/wiki/Minimum_total_potential_energy_principle Wikipedia: Prinzip vom Minimum der Potentiellen Energie] | |||
'''Gelöste Aufgaben''' | |||
{{Special:PrefixIndex/Category:}} | |||
{{#categorytree:Anfangswertproblem|mode=parents}} | |||
Aktuelle Version vom 18. Februar 2021, 07:11 Uhr
Die Aussage
Die Aussage des Prinzips ist anschaulich:
Von allen Zuständen, die ein System einnehmen kann, ist derjenige ein Gleichgewichtszustand, der die potentielle Energie des Systems minimiert.
Also:
Bei einfachen Systemen besteht U meist aus
mit dem Potential einer Kraft (V=-A) oder der Arbeitsfunktion (A) am System und der gespeicherten Energie der inneren Kräfte - der Formänderungsenergie Π.
Bei Aufgaben der Mechanik, bei denen Kräfte und Spannungen linear von den gesuchten Koordinaten abhängen, ist das Potential der Energie eines System immer eine quadratische Form:
Für die Lösung nutzen wir unsere Überlegungen zu Minimum Prinzipen.
Hieraus kommt: U hat ein Minimum, wenn q
erfüllt.
Beispiel:
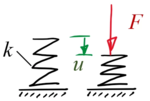
Eine Feder (Steifigkeit k) wird durch die Kraft F belastet.
Berechnen Sie die Federkompression u.
Lösung mit Maxima
Die gesamte potentielle Enerfie des Systems ist die Formänderungsenergie Π minus dem Potential A der äußeren, eingeprägten Kraft F.
Einsetzen liefert
und diese Funktion können wir plotten.
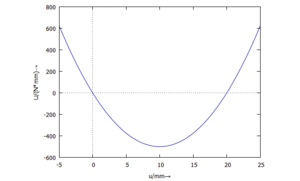
Offensichtlich hat U ein Minimum bei u=10 mm und das muss auch aus der Gleichgewichtsbeziehung
herauskommen - und das tut es auch:
/* Maxima */
params: [k=10*N/mm, F=100*N];
PMPE : U = Pi-A;
potEnergy : [A = F*u, Pi=1/2*k*(-u)^2];
/* potential energy */
PMPE : subst(potEnergy,PMPE);
/* plot U */
plot2d(subst([u=upsilon*mm],subst(params,subst(PMPE,U/(N*mm)))),
[upsilon,-5,25],
[xlabel, "u/mm→"], [ylabel, "U/(N*mm)→"]);
/* equilibrium condition */
equ : diff(subst(PMPE,U),u)=0;
sol: solve(equ, u)[1]
Anwendung für Kontinua
Die Formänderungsenergie für Kontinua besteht besonders bei Stab-Modellen aus einem charakteristischen quadratischen Term, den wir uns hier anhand des Euler-Bernoulli-Balkens anschauen.
So setzten wir bei Näherungslösungen in den Ausdruck
die Näherungslösung
mit dem gesuchten Wichtungsfaktor Wi und den Trial-Functions
Für das Näherungsverfahren, müssen diese Funktionen linear unabhängig voneinander sein und den geometrischen (oder essentiellen) Randbedingungen genügen.
Ansonsten dürfen es beliebig viele sein, wir erhalten also Gleichungssysteme für entsprechend viele Wi.
Charakteristisch für das Verfahren vom Minimum der Potentiellen Energie - wie auch dem Prinzip der virtuellen Verrückungen - ist das Entstehen von Integralen mit Paaren von Integranden aus den Trial-Functions. So ist
Diesen Ausdruck können wir umschreiben als
mit
- .
Diesen Umstand nutzen wir beim Aufstellen der Bewegungsgleichungen mit dem Rechner (vgl. conv→ )
Links
Gelöste Aufgaben
- A*x=b
- Achsensymmetrie
- Analytische Lösung
- Anfangswertproblem
- Ansys
- Arbeitsfunktion
- Axiom
- Biege-Belastung
- Computer
- Dehnstab
- Dimensionslose Schreibweise
- Draft
- Dynamik
- D’Alembertsches Prinzip
- Eigenvektor
- Eigenwert
- Eigenwertproblem
- Englisch
- Euler-Bernoulli-Balken
- Feder-Masse-System
- Fehlerquadratsumme
- Finite-Differenzen-Methode
- Finite-Elemente-Methode
- Floquet-Theorem
- Formänderungsenergie
- Freischneiden
- Fundamentalmatrix
- Gelöste Aufgaben
- Geometrische Zwangsbedingung
- Haften und Reiben
- Hauptspannung
- Innovation
- Kennlinie
- Knotenpunktverfahren
- Koordinaten
- Kreisel
- Lagrange-Multiplikator
- Lernvideo
- Lexikon
- Lineare Algebra
- Mathieusche Differentialgleichung
- Matlab
- Maxima
- Mechatronik
- Membranspannung
- Modalanalyse
- Newtonverfahren
- Nichtlineare Schwingungen
- Numerische Lösung
- Parametererregte Schwingungen
- Potential
- Prinzip der virtuellen Arbeit
- Prinzip der virtuellen Verrückungen
- Prinzip vom Minimum der Potentiellen Energie
- Randwertproblem
- Rayleigh-Ritz-Prinzip
- Rotationssymmetrie
- Runge-Kutta-Verfahren
- Schwingungen von Kontinua
- Shell-Element
- Smartphone
- Stab
- Stabilität
- Stabwerk
- Starrer Körper
- Statik
- Stick-Slip-Effekt
- Timoshenko-Balken
- Totzeit
{{#categorytree:Anfangswertproblem|mode=parents}}