Werkzeuge/Beschreibung physikalischer Systeme/Dimensionen und Einheiten: Unterschied zwischen den Versionen
Die Seite wurde neu angelegt: „M“ |
Keine Bearbeitungszusammenfassung |
||
| (Eine dazwischenliegende Version desselben Benutzers wird nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
M | [[Category:Dimensionslose Schreibweise]] | ||
=== Schreibweise === | |||
Die Dimension einer physikalischen Größe erfasst man durch | |||
::<math>\text{ dim}(.)</math> | |||
So ist | |||
::<math>\text{ dim}(F) = \text{Kraft}</math> | |||
oder, abgekürzt | |||
::<math>\begin{array}{lcl}\text{ dim}(F) &=& K(\text{Kraft})\\\text{ dim}(\ell) &=& L (\text{Länge})\\\text{ dim}(t) &=& T (\text{Zeit}) \\\text{ dim}(m) &=& M (\text{Masse} ) \end{array}</math> | |||
Basis-Einheiten nach dem SI-System sind | |||
# Meter (''m''), | |||
# Kilogramm (''kg''), | |||
# Sekunde (''s''), | |||
# Ampere (''A''), | |||
# Kelvin (K), | |||
# Mol (mol) sowie | |||
# Candela (cd) | |||
Von diesen sieben brauchen wir hier nur die ersten drei. | |||
Weitere Einheiten lassen sich auf diese drei zurückführen und umrechnen: | |||
::<math>N = \displaystyle \frac{kg \; m}{s^2}</math>, | |||
::<math>\text{ rad } = 1 \displaystyle \frac{m}{m} (\text{ radiant })</math> | |||
oder | |||
::<math>\text{bar} = \displaystyle 10^5 \frac{N}{m^2}</math>. | |||
Im Computer können wir keine Einheiten brauchen. Wir könnten alle Parameter in den SI-Basiseinheiten ausdrücken - dann müssen sich die Einheiten herauskürzen. Das geht bei realen Problemen häufig schief, weil die dann in den Systemmatrizen stehenden numerische Werte oft um mehrere Größenordnungen unterschiedliche Werte haben. | |||
Beispiel: | |||
Die numerischen Werte in der Randbedingung des [[Sources/Lexikon/Euler-Bernoulli-Balken|Euler-Bernoulli-Balkens]] | |||
* für das Moment sind von der Größenordnung 10^6; | |||
* für die Verschiebung/Verdrehung sind von der Größenordnung 1. | |||
=== Dimensionslos-Machen von Bewegungsgleichungen === | |||
Wir suchen nach Koordinaten der Bewegung, die keine Einheit mehr haben und deren Werte von der Größenordnung "1" sind. Das klappt nicht immer, aber oft. | |||
Vorgehensschema: | |||
# alle dimensionsbehafteten Parameter und Koordinaten durch dimensionslose Größen und Bezugsgrößen ersetzen; | |||
# die Bezugsgrößen aus den Bewegungsgleichungen herauskürzen → die Bewegungsgleichung sieht wieder wie ursprünglich aus; | |||
# Bezugsgrößen "passend" wählen; | |||
# die numerischen Werte aller dimensionslosen Parameter berechnen und in die Bewegungsgleichungen einsetzen; | |||
# Bewegungsgleichungen lösen. | |||
==== Beispiel: ==== | |||
===== Aufgabenstellung ===== | |||
Wir lassen eine Kugel im Erdschwerefeld aus der Höhe H und ohne Anfangsgeschwindigkeit fallen. | |||
[[Datei:DimensionenUndEiheiten-BallBounce.png|mini|188x188px|Lageplan]] | |||
Die Bewegungsgleichung des Systems mit der nichtlinearen Kontaktkraft ''K(h)'' in ''h(t)'' lautet: | |||
::<math>-m \ddot{h} - m g + K(h) = 0</math>, | |||
===== Dimensionslose Koordinate ===== | |||
Eine dimensionslose Koordinate bekommen wir, wenn wir ''h'' durch eine passende Bezugslänge ''l<sub>Bez</sub>'' teilen, also | |||
::<math>\tilde{h} = \displaystyle \frac{h(t)}{\ell_{Bez}} \text{ bzw } h = \tilde{h} \cdot \ell_{Bez}</math>, | |||
Die zweite Ableitung nach der Zeit bringt uns allerdings wieder eine Dimension - hier die Zeit - hinein. Mit der neuen, dimensionslosen Zeit τ | |||
::<math>\tau = \displaystyle \frac{t}{t_{Bez}}</math>, | |||
und den dimensionslosen Parametern | |||
::<math>\displaystyle \tilde{m} = \frac{m}{m_{Bez}}, \tilde{K} = \frac{K}{F_{Bez}} \text{ und } \tilde{g} = \frac{g}{a_{Bez}} </math>, | |||
lautet die neue Bewegungsgleichung nun | |||
::<math>\displaystyle - \tilde{m} \frac{m_{Bez} \ell_{Bez}}{t_{Bez}^2} \frac{d^2}{d \tau^2} \tilde{h} - m_{Bez} a_{Bez} \tilde{m} \tilde{g} + F_{Bez} \tilde{K} = 0</math>, | |||
Das sieht sehr kompliziert aus - löst sich aber gleich in Wohlgefallen auf. Zunächst dürfen wir nur drei Beszugsgrößen unabhängig voneinander wählen, also könnten wir | |||
::<math>\displaystyle a_{Bez} = \frac{\ell_{Bez}}{t_{Bez}^2} \text{ und } F_{Bez} = \frac{m_{Bez} \ell_{Bez}}{t_{Bez}^2}</math>, | |||
ersetzen und erhalten - nach der Division durch die Bezugskraft | |||
::<math>-\tilde{m} \tilde{h}'' - \tilde{m} \tilde{g} + \tilde{K} = 0\text{ mit } \displaystyle (.)' := \frac{d}{d\tau}(.)</math>, | |||
Das ist nun wiederum die Form der Ausgangs-Bewegungsgleichung - nur, dass hier jetzt andere Zahlenwerte stehen. | |||
===== Wahl der Bezugsgrößen ===== | |||
Es ist praktisch | |||
::<math>\displaystyle \ell_{Bez} = H \text{ , } F_{Bez} = m g \text{ und } t_{Bez} = \sqrt{\frac{2 H}{g}} (\text{ die Zeit bis zum ersten Aufprall})</math>, | |||
zu wählen - denn dann wird der Wert von der dimensionslosen Koordinate ''h(t)/H'' zwischen 0 und 1 sein, die Dauer einer Periode des Vorgangs wird fast 2 sein (wenn die Stoßdauer sehr kurz ist). | |||
Mit den Systemparametern | |||
::<math>H = 1 \text{m}, m g = 1 \text{N}</math>, | |||
ist z.B. der Zahlenwert für die dimensionslose Erdbeschleunigung nun | |||
::<math>\begin{array}{cl} \tilde{g} &=\displaystyle 9.81 \frac{\text{m}}{\text{s}^2}/\frac{\ell_{Bez}}{t_{Bez}^2}\\ &= 1.962 \end{array}</math>, | |||
===== Bewegungsgleichungen lösen ===== | |||
Die Bewegungsgleichung können wir nun als ODE 1ster Ordnung schreiben als | |||
::<math>\displaystyle \frac{d}{d\tau}\left( \begin{array}{c} \tilde{h} \\ \tilde{v} \end{array} \right) = \left( \begin{array}{c} \tilde{v} \\-\tilde{g}+\tilde{k}(\tilde{h}) \end{array} \right)</math>, | |||
und im Zeitbereich mit den Anfangsbedingungen | |||
::<math>\left( \begin{array}{c} \tilde{h}_0 \\ \tilde{v}_0 \end{array} \right) = \left( \begin{array}{c} 1\\0 \end{array} \right)</math>, | |||
lösen. Im Zeitbereich finden wir die Lösung | |||
[[Datei:DimensionenUndEinheiten-Simulationsergebnis.png|left|mini|Zeitverlauf der Ball-Höhe.]] | |||
und die entspricht - mit der Anfangs-Höhe "1" und der Periodendauer von (fast) "2" - genau unseren Vorstellungen! | |||
Aktuelle Version vom 25. März 2021, 15:22 Uhr
Schreibweise
Die Dimension einer physikalischen Größe erfasst man durch
So ist
oder, abgekürzt
Basis-Einheiten nach dem SI-System sind
- Meter (m),
- Kilogramm (kg),
- Sekunde (s),
- Ampere (A),
- Kelvin (K),
- Mol (mol) sowie
- Candela (cd)
Von diesen sieben brauchen wir hier nur die ersten drei.
Weitere Einheiten lassen sich auf diese drei zurückführen und umrechnen:
- ,
oder
- .
Im Computer können wir keine Einheiten brauchen. Wir könnten alle Parameter in den SI-Basiseinheiten ausdrücken - dann müssen sich die Einheiten herauskürzen. Das geht bei realen Problemen häufig schief, weil die dann in den Systemmatrizen stehenden numerische Werte oft um mehrere Größenordnungen unterschiedliche Werte haben.
Beispiel:
Die numerischen Werte in der Randbedingung des Euler-Bernoulli-Balkens
- für das Moment sind von der Größenordnung 10^6;
- für die Verschiebung/Verdrehung sind von der Größenordnung 1.
Dimensionslos-Machen von Bewegungsgleichungen
Wir suchen nach Koordinaten der Bewegung, die keine Einheit mehr haben und deren Werte von der Größenordnung "1" sind. Das klappt nicht immer, aber oft.
Vorgehensschema:
- alle dimensionsbehafteten Parameter und Koordinaten durch dimensionslose Größen und Bezugsgrößen ersetzen;
- die Bezugsgrößen aus den Bewegungsgleichungen herauskürzen → die Bewegungsgleichung sieht wieder wie ursprünglich aus;
- Bezugsgrößen "passend" wählen;
- die numerischen Werte aller dimensionslosen Parameter berechnen und in die Bewegungsgleichungen einsetzen;
- Bewegungsgleichungen lösen.
Beispiel:
Aufgabenstellung
Wir lassen eine Kugel im Erdschwerefeld aus der Höhe H und ohne Anfangsgeschwindigkeit fallen.
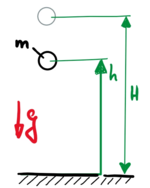
Die Bewegungsgleichung des Systems mit der nichtlinearen Kontaktkraft K(h) in h(t) lautet:
- ,
Dimensionslose Koordinate
Eine dimensionslose Koordinate bekommen wir, wenn wir h durch eine passende Bezugslänge lBez teilen, also
- ,
Die zweite Ableitung nach der Zeit bringt uns allerdings wieder eine Dimension - hier die Zeit - hinein. Mit der neuen, dimensionslosen Zeit τ
- ,
und den dimensionslosen Parametern
- ,
lautet die neue Bewegungsgleichung nun
- ,
Das sieht sehr kompliziert aus - löst sich aber gleich in Wohlgefallen auf. Zunächst dürfen wir nur drei Beszugsgrößen unabhängig voneinander wählen, also könnten wir
- ,
ersetzen und erhalten - nach der Division durch die Bezugskraft
- ,
Das ist nun wiederum die Form der Ausgangs-Bewegungsgleichung - nur, dass hier jetzt andere Zahlenwerte stehen.
Wahl der Bezugsgrößen
Es ist praktisch
- ,
zu wählen - denn dann wird der Wert von der dimensionslosen Koordinate h(t)/H zwischen 0 und 1 sein, die Dauer einer Periode des Vorgangs wird fast 2 sein (wenn die Stoßdauer sehr kurz ist).
Mit den Systemparametern
- ,
ist z.B. der Zahlenwert für die dimensionslose Erdbeschleunigung nun
- ,
Bewegungsgleichungen lösen
Die Bewegungsgleichung können wir nun als ODE 1ster Ordnung schreiben als
- ,
und im Zeitbereich mit den Anfangsbedingungen
- ,
lösen. Im Zeitbereich finden wir die Lösung
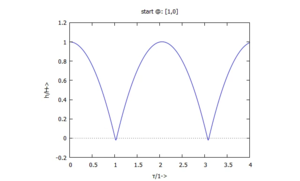
und die entspricht - mit der Anfangs-Höhe "1" und der Periodendauer von (fast) "2" - genau unseren Vorstellungen!