Gelöste Aufgaben/MaMa: Unterschied zwischen den Versionen
Die Seite wurde neu angelegt: „Category:Gelöste Aufgaben Category:Dimensionslose Schreibweise Category:A*x=b Category:Lineare Algebra Category:Analytische Lösung Category:Numerische Lösung Category:Randwertproblem Category:Euler-Bernoulli-Balken Category:Matlab Category:Maxima Category:Statik ==Aufgabenstellung== Ein Stab der Länge <math>3a</math> und Biegesteifigkeit <math>EI</math> ist links fest eingespannt und wird bei 2/3 sein…“ |
Keine Bearbeitungszusammenfassung |
||
| (20 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 13: | Zeile 13: | ||
==Aufgabenstellung== | ==Aufgabenstellung== | ||
Ein Stab der Länge <math>3a</math> und Biegesteifigkeit <math>EI</math> ist links fest eingespannt und wird bei 2/3 seiner Länger durch ein gelenkiges Lager gestützt. | Ein Stab der Länge <math>3a</math> und Biegesteifigkeit <math>EI</math> ist links fest eingespannt und wird bei 2/3 seiner Länger durch ein gelenkiges Lager gestützt. | ||
Zwischen dem freien rechten Rand und dem gelenkigen Lager wirkt eine Streckenlast <math>q_0</math>. | Zwischen dem freien rechten Rand und dem gelenkigen Lager wirkt eine konstante Streckenlast <math>q_0</math>. | ||
<onlyinclude> | <onlyinclude> | ||
[[Datei:MaMa-01.png| | [[Datei:MaMa-01.png|250px|left|mini|Lageplan]] | ||
Gesucht ist | Gesucht ist die analytische Lösung für den Euler-Bernoulli-Balken und die Verläufe der Schnittgrößen. Im Vordergrund der Ausarbeitung steht das Zusammenspiel von Maxima (Computeralgebra) und Matlab (Numerik) zum Aufstellen, Verwalten und Lösen des linearen Gleichungssystems. | ||
</onlyinclude> | </onlyinclude> | ||
Die Aufgabe ist einfach genug, um sie analytisch mit Maxima allein zu lösen. Hier geht es aber darum, die "Zusammenarbeit" zwischen den beiden Software-Paketen exemplarisch vorzustellen. Dieses Zusammenspiel wird dann interessant, wenn die Anzahl der Gleichungen groß wird - typischer weise > 50. Dann ist eine algebraische Lösung oft nicht mehr praktikabel. Maxima eignet sich dann hervorragend für das Aufstellen und Verwalten der Gleichungen. Die konsolidierten Gleichungen werden dann zur numerischen Lösung an Matlab übergeben. | |||
Wie das geht, zeigen wir hier. | |||
== | == Lösung mit Maxima und Matlab == | ||
Im folgenden finden Sie die Skripte für Maxima und Matlab, mit denen diese Aufgabe bearbeitet wurde. | |||
=== Declarations === | |||
[[Datei:MaMa-11.png|350px|right|mini|Bezeichnung für Bereiche und Knoten.]] | |||
Wir zeichnen zunächst die Bereiche, Knoten und Koordinaten aus: | |||
Für Bereich <math>I</math> (zwischen <math>A</math> und <math>B</math>) führen wir die unabhängige Koordinate <math>x_I</math> ein, für Bereich <math>II</math> (zwischen <math>B</math> und <math>C</math>) die Koordinate <math>x_{II}</math>. | |||
Die zwei Bereiche haben die Längen | |||
* <math>\ell_I</math> und | |||
* <math>\ell_{II}</math>. | |||
Um die gesuchte Lösung dimensionslos ansetzten zu können, wählen wir eine Vergleichslösung. Hier bietet sich der [[Sources/Lexikon/Euler-Bernoulli-Balken/Standard-Lösungen#Kragbalken_Streckenlast|Kragbalken unter Streckenlast]] an. Diese liefert für die maximale Auslenkung von <math>w(x)</math> und die maximlae Kippung der Querschnitte von <math>\phi(x)</math> | |||
* <math>w_{ref} = \frac{q_{0} a^4}{8 EI}</math> und | |||
* <math>\varphi_{ref} = \frac{q_0 a^3}{6 EI}</math> | |||
Unsere Lösung für <math>w(x)</math> teilen wir dann durch <math>w_{ref}</math> - und erhalten eine Aussage darüber, wie groß die Auslenkung unseres Systems im Vergleich zur Referenz-Auslenkung ist. Und dieses Verhältnis ist eine Zahl - ohne Parameter - so dass wir sie einfach interpretieren können. | |||
Zusätzlich wählen wir | |||
* <math>M_{ref} = \frac{q_{0} a^2}{2}</math> und | |||
* <math>Q_{ref} = q_0 a</math> | |||
für die Ergebnisse von <math>Q(x)</math> und <math>M(x)</math>. | |||
=== Boundary Value Problem === | |||
Das Randwertproblem wird im Feld von der Euler-Bernoulli-Differentialgleichung des Balkens und an den Rändern durch kinematische oder Kraft-Randbedingungen beschrieben. | |||
==== Differentialgleichung des Euler-Bernoulli-Balkens ==== | |||
Die Gleichgewichtsbedingung am Balken führt auf die Differentialgleichung | |||
::<math>EI w^{IV}=q_0</math> | |||
Deren allgemeine Lösung (also ohne Anpassung an Rand- und Übergangsbedingungen) ist | |||
<table class="wikitable" style="background-color:white; margin-right:14px;"><tr> | |||
<td>... für die Auslenkung des Querschnitts:</td> | |||
<td> | |||
<math> EI w(x)=\frac{1}{24} q_0 x^4 + | |||
\frac{1}{ 6} C_3 x^3 + | |||
\frac{1}{ 2} C_2 x^2 + | |||
C_1 x + | |||
C_0 | |||
</math></td></tr> | |||
</table> | |||
mit den 4 Integrationskonstanten - und damit unseren Unbekannten je Abschnitt - | |||
::<math> C_0, C_1, C_2 \text{ und } C_3 | |||
</math>. | |||
Aus Gleichgewichts- und Kinematik-Beziehungen kommen dann die weiteren Gleichungen | |||
<table class="wikitable" style="background-color:white; margin-right:14px;"> | |||
<tr><td>... für den Kippwinkel des Querschnitts:</th><td><math> | |||
EI \varphi(x) = EI \frac{dw}{dx} | |||
=+\frac{1}{ 6} q_0 x^3 | |||
+\frac{1}{ 2} C_3 x^2 | |||
+ C_2 x | |||
+ C_1</math></td></tr> | |||
<tr><td>... für das Biegemoment:</td><td><math> | |||
M(x) =- EI \frac{d^2w}{dx^2} | |||
=-\frac{1}{ 2} q_0 x^2 | |||
- C_3 x | |||
- C_2 </math> und</td></tr> | |||
<tr><td>... für die Querkraft:</td><td><math> | |||
Q(x) =\frac{dM}{dx} | |||
=- q_0 x | |||
- C_3 </math>.</td></tr> | |||
</table> | |||
In unserer Aufgabe haben wir zwei Bereiche: in B müssen wir diese allgemeinen Lösungen aneinander anstückeln. Um sie zu unterscheiden, hängen wir für jede Lösung den Index des Bereichs an, also | |||
<table class="wikitable style="background-color:white; float: left; margin-right:14px;"><tr> | |||
<th>Bereich I<br><math>0<x_I<\ell_I</math> | |||
</th> | |||
<th>Bereich II<br><math>0<x_{II}<\ell_{II}</math></th></tr> | |||
<tr><td> | |||
::<math> EI w_I(x)=\frac{1}{24} q_{I,0} x_I^4 + | |||
\frac{1}{ 6} C_{I,3} x_I^3 + | |||
\frac{1}{ 2} C_{I,2} x_I^2 + | |||
C_{I,1} x + | |||
C_{I,0} | |||
</math></td><td> | |||
::<math> EI w_{II}(x)=\frac{1}{24} q_{II,0} x_I^4 + | |||
\frac{1}{ 6} C_{II,3} x_I^3 + | |||
\frac{1}{ 2} C_{II,2} x_I^2 + | |||
C_{II,1} x + | |||
C_{II,0} | |||
</math></td></tr> | |||
</table> | |||
Und das gilt in gleicher Weise für die Gleichungen von <math>\varphi, M, Q</math>. | |||
==== Rand- und Übergangsbedingungen ==== | |||
Die Rand- und Übergangsbedingungen im Stab finden wir entweder aus kinematischen Überlegungen oder aus Gleichgewichtsbeziehungen mit den Schnittkräften des Balkens. | |||
'''Kinematische Rand- und Übergangsbedingungen''' | |||
[[Datei:MaMa-14.png|350px|right|mini|Angenommene Verformung des Stabes.]]Für die Kinematik des Systems schauen wir uns die angenommene Verformung des Systems an: | |||
Aus dem Bild entnehmen wir, dass | |||
* ... in A: | |||
** <math>w_I(0) = 0</math> | |||
** <math>\varphi_I(0) = 0</math> | |||
* ... in B:[[Datei:MaMa-13.png|120px|right|mini|Kippwinkel bei "B".]] | |||
** <math>w_I(\ell_I) = 0</math> | |||
** <math>w_{II}(0) = 0</math> und | |||
** <math>\varphi_I(\ell_I) = \varphi_{II}(0) = \Phi_B</math> | |||
gilt. | |||
'''Kraft- und Momenten Rand- und Übergangsbedingungen''' | |||
Für die Übergangsbedingungen in B brauchen wir ein Freikörperbild: [[Datei:MaMa-12.png|180px|right|mini|Schnittbild in B.]] | |||
Die Gleichgewichtsbeziehungen erhalten wir dann zu | |||
* ... in B: | |||
** <math>M_I(\ell_I) = M_{II}(\ell_{II})</math> und | |||
* ... in C (freier Rand): | |||
** <math>Q_{II}(\ell_II) = 0</math> | |||
** <math>M_{II}(\ell_II) = 0</math> | |||
Dies sind insgesamt 5+3=8 Rand- bzw. Übergangsbedingungen für die 8 Integrationskonstanten | |||
::<math> C_{I,0}, C_{I,1}, C_{I,2}, C_{I,3}, C_{II,0}, C_{II,1}, C_{II,2} \text{ und } C_{II,3} </math>. | |||
=== Konsolidierung der Gleichungen === | |||
Jetzt kommt Maxima ins Spiel. | |||
<!--------------------------------------------------------------------------------> | <!--------------------------------------------------------------------------------> | ||
{{MyCodeBlock|title= | {{MyCodeBlock|title=Maxima-Quellcode | ||
|text= | |text= | ||
Im Quellcode für Maxima werden die Elemente aus dem Lösungsprozess oben direkt umgesetzt. So finden sich in "fcts" die Funktionen für | |||
<math>w, \varphi, M, Q</math>. | |||
Diese Funktionen können wir mit Maxima direkt in den Randbedingungen ansprechen und erhalten die Gleichungen | |||
::<math> | |||
\begin{array}{lccl} | |||
1)&C_{I,0}/EI&=&0\\ | |||
2)&C_{I,1}/EI&=&0\\ | |||
3)&4 C_{I,3} a^3/(3 EI)+2 C_{I,2} a^2/EI+2 C{I,1} a/EI + C_{I,0}/EI&=&0\\ | |||
4)&2 C_{1,3} a^2/EI+2 C_{I,2} a/EI+C_{1,1}/EI &=& C_{II,1}/EI\\ | |||
5)& -2 C_{I,3} a - C_{I,2} &=& -C_{II,2}\\ | |||
6)& C_{II,0}/EI&=&0\\ | |||
7)&-q_{0} a^2/2 - C_{II,3} a - C_{II,2}&=&0\\ | |||
8)&- q_{0} a-C_{II,3} &=& 0 | |||
\end{array} | |||
</math> | |||
Diese Gleichungen kann man einzeln mit passenden Faktoren - z.B. <math>EI</math> - durchmultiplizieren und man erhält das einfacher aussehende lineare Gleichungssystem | |||
::<math> | |||
\begin{pmatrix}1 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ | |||
0 & 1 & 0 & 0 & 0 & 0 & 0 & 0\\ | |||
1 & 2 a & 2 {{a}^{2}} & \frac{4 {{a}^{3}}}{3} & 0 & 0 & 0 & 0\\ | |||
0 & 1 & 2 a & 2 {{a}^{2}} & 0 & -1 & 0 & 0\\ | |||
0 & 0 & -1 & -\left( 2 a\right) & 0 & 0 & 1 & 0\\ | |||
0 & 0 & 0 & 0 & 1 & 0 & 0 & 0\\ | |||
0 & 0 & 0 & 0 & 0 & 0 & -1 & -a\\ | |||
0 & 0 & 0 & 0 & 0 & 0 & 0 & -1\end{pmatrix} \cdot | |||
\begin{pmatrix}{C_{I,0}}\\ | |||
{C_{I,1}}\\ | |||
{C_{I,2}}\\ | |||
{C_{I,3}}\\ | |||
{C_{II,0}}\\ | |||
{C_{II,1}}\\ | |||
{C_{II,2}}\\ | |||
{C_{II,3}} | |||
\end{pmatrix} = | |||
\begin{pmatrix}0\\ | |||
0\\ | |||
0\\ | |||
0\\ | |||
0\\ | |||
0\\ | |||
\frac{{q_{0}} {{a}^{2}}}{2}\\ | |||
{q_{0}} a | |||
\end{pmatrix} | |||
</math> | |||
Maxima hilft auch dabei, die von Null verschiedenen Elemente herauszusortieren und für Matlab zu formatieren für <math>\underline{\underline{A}}</math>: | |||
<pre> | |||
A( 1 , 1 ) = 1; | |||
A( 2 , 2 ) = 1; | |||
A( 3 , 1 ) = 1; | |||
A( 3 , 2 ) = 2*a; | |||
A( 3 , 3 ) = 2*a^2; | |||
A( 3 , 4 ) = (4*a^3)/3; | |||
A( 4 , 2 ) = 1; | |||
A( 4 , 3 ) = 2*a; | |||
A( 4 , 4 ) = 2*a^2; | |||
A( 4 , 6 ) = -1; | |||
A( 5 , 3 ) = -1; | |||
A( 5 , 4 ) = -(2*a); | |||
A( 5 , 7 ) = 1; | |||
A( 6 , 5 ) = 1; | |||
A( 7 , 7 ) = -1; | |||
A( 7 , 8 ) = -a; | |||
A( 8 , 8 ) = -1; | |||
</pre> | |||
und <math>\underline{b}</math>: | |||
<pre> | |||
b(7,1) = q0*a^2/2; | |||
b(8,1) = q0*a; | |||
</pre> | |||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
1+1 | /*+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++*/ | ||
/* Modul Numerische Methoden der Mechanik */ | |||
/* Script zum Unterricht */ | |||
/* Löst: Gross e.a., Technische Mechanik, Bd 2, A 3.16 */ | |||
/* Autor: Andreas Baumgart */ | |||
/* Last Updated: 2024-11-13 */ | |||
/*+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++*/ | |||
/* parameters */ | |||
params: [ℓ[1]=2*a, ℓ[2]=a, q[1,0]=0]; | |||
/* reference-values */ | |||
refs: [w[ref]=q[2,0]*a^4/8/EI, | |||
φ[ref]=q[2,0]*a^3/6/EI, | |||
M[ref]=q[2,0]*a^2/2, | |||
Q[ref]=q[2,0]*a]; | |||
/*****************************************/ | |||
/* the differential equation for the EBB */ | |||
ebb: [EI*diff(w[i](x),x,4)=0, w[i](x) = 1/EI*(q[i,0]*x^4/24+sum(1/j!*C[i,j]*x^j,j,0,3))]; | |||
/* ... and its solution */ | |||
fcts: [w[i](x) = diff(subst(ebb,w[i](x)),x,0), | |||
φ[i](x) = diff(subst(ebb,w[i](x)),x,1), | |||
M[i](x) =-EI*diff(subst(ebb,w[i](x)),x,2), | |||
Q[i](x) =-EI*diff(subst(ebb,w[i](x)),x,3)]; | |||
/* boundary conditions */ | |||
bvp: [subst([i=1,x= 0 ], subst(fcts,w[i](x))) = 0, | |||
subst([i=1,x= 0 ], subst(fcts,φ[i](x))) = 0, | |||
subst([i=1,x=ℓ[1]], subst(fcts,w[i](x))) = 0, | |||
subst([i=1,x=ℓ[1]], subst(fcts,φ[i](x))) = subst([i=2,x= 0 ], subst(fcts,φ[i](x))), | |||
subst([i=1,x=ℓ[1]], subst(fcts,M[i](x))) = subst([i=2,x= 0 ], subst(fcts,M[i](x))), | |||
subst([i=2,x= 0 ], subst(fcts,w[i](x))) = 0, | |||
subst([i=2,x=ℓ[2]], subst(fcts,M[i](x))) = 0, | |||
subst([i=2,x=ℓ[2]], subst(fcts,Q[i](x))) = 0]; | |||
X: flatten(makelist(makelist(C[i,j],j,0,3),i,1,2)); | |||
/* scale equations - so they look nicer ... */ | |||
scale: [EI,EI,EI,EI,1,EI,1,1]; | |||
for i:1 thru length(bvp) do | |||
bvp[i]: subst(params,bvp[i])*scale[i]; | |||
/* preprocess */ | |||
bvp: expand(subst(refs,subst(params,bvp))); | |||
ACM: augcoefmatrix(bvp,X); | |||
A: submatrix(ACM,9); | |||
b:-col(ACM,9); | |||
print(A,"*",transpose(X),"=",b)$ | |||
/* you'll need to transfere these coefficients to Matlab: */ | |||
for row:1 thru 8 do | |||
for col:1 thru 8 do | |||
if notequal(subst(a=1,A[row][col]), 0) then | |||
print("A(",row,",",col,") = ", A[row][col])$ | |||
/* Output for Matlab ..... | |||
A( 1 , 1 ) = 1; | |||
A( 2 , 2 ) = 1; | |||
A( 3 , 1 ) = 1; | |||
A( 3 , 2 ) = 2*obj.a; | |||
A( 3 , 3 ) = 2*obj.a^2; | |||
A( 3 , 4 ) = (4*obj.a^3)/3; | |||
A( 4 , 2 ) = 1; | |||
A( 4 , 3 ) = 2*obj.a; | |||
A( 4 , 4 ) = 2*obj.a^2; | |||
A( 4 , 6 ) = -1; | |||
A( 5 , 3 ) = -1; | |||
A( 5 , 4 ) = -(2*obj.a); | |||
A( 5 , 7 ) = 1; | |||
A( 6 , 5 ) = 1; | |||
A( 7 , 7 ) = -1; | |||
A( 7 , 8 ) = -obj.a; | |||
A( 8 , 8 ) = -1; | |||
*/ | |||
/* solve */ | |||
/* we could also solve in Maxima : */ | |||
sol: solve(bvp,X)[1]; | |||
/* postprocess - an example: */ | |||
toPlot: expand(subst([x=ξ*a],subst(refs,subst(params,subst(sol,makelist(subst([i=j],subst(fcts, w[i](x)/w[ref])),j,1,2)))))); | |||
/* plot dimensionless displacements of beams in secsions I und II */ | |||
print("reference displacement w[ref] = ", subst(refs,w[ref]))$ | |||
plot2d([[parametric,ξ,toPlot[1],[ξ,0,2]],[parametric,2+ξ,toPlot[2],[ξ,0,1]]],[xlabel,"x/a->"],[ylabel,"w/w[ref]->"], [legend, "w_1", "w_2"]); | |||
/* these are the functions needed in postprocessing in Matlab : */ | |||
for k:1 thru 4 do | |||
(print(" for ", lhs(fcts[k])/lhs(refs[k]),":"), | |||
print(expand(subst([x=ξ*a],subst(params,makelist(subst([i=j],subst(refs,subst(fcts, lhs(fcts[k])/lhs(refs[k])))),j,1,2))))))$ | |||
/* note that x=xi*a has been introduced as the dimensionless coordinate */ | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
< | <!--------------------------------------------------------------------------------> | ||
< | |||
< | {{MyZipfileBlock | ||
</ | |title=Matlab<sup>©</sup>-Quellcode | ||
|text = | |||
Genau so wird der Code dann in Matlab eingefügt - hier mit der Änderung, dass <math>a</math> und <math>q_0</math> Properties der EBB-Class sind und entsprechend innerhalb der Klasse als obj.a bzw obj.q angesprochen werden müssen, also | |||
<syntaxhighlight lang="matlab" line start=1> | |||
: | |||
: | |||
function A = sysmat(obj) | |||
%populate | |||
% system matrix A | |||
% create matrix | |||
A = zeros(8,8); | |||
% populate matrix (only non-zero elements) | |||
A( 1 , 1 ) = 1; | |||
A( 2 , 2 ) = 1; | |||
A( 3 , 1 ) = 1; | |||
A( 3 , 2 ) = 2*obj.a; | |||
A( 3 , 3 ) = 2*obj.a^2; | |||
A( 3 , 4 ) = (4*obj.a^3)/3; | |||
A( 4 , 2 ) = 1; | |||
A( 4 , 3 ) = 2*obj.a; | |||
A( 4 , 4 ) = 2*obj.a^2; | |||
A( 4 , 6 ) = -1; | |||
A( 5 , 3 ) = -1; | |||
A( 5 , 4 ) = -(2*obj.a); | |||
A( 5 , 7 ) = 1; | |||
A( 6 , 5 ) = 1; | |||
A( 7 , 7 ) = -1; | |||
A( 7 , 8 ) = -obj.a; | |||
A( 8 , 8 ) = -1; | |||
end | |||
function b = rhs(obj) | |||
%populate | |||
% right-hand side | |||
% cretae matrix | |||
b = zeros(8,1); | |||
% populate matrix | |||
b(7,1) = obj.q*obj.a^2/2; | |||
b(8,1) = obj.q*obj.a; | |||
end | |||
: | |||
: | |||
</syntaxhighlight> | |||
[[Datei:MaMa-folder-structure.png|links|mini|Folder Structure]]Die Datei-Struktur links zeigt das Skript <nowiki>MaMa.m</nowiki> sowie Classes und Functions in den jeweiligen Ordnern. Die Excel-Datei enthält alle System-Parameter. | |||
Den komplette Quellcode zu diesem Programm können Sie über dieses ZIP-File rechts herunterladen. | |||
|file=MaMa.zip}} | |||
=== Solving === | |||
Die Gleichungen lösen wir in Maxima mit dem Befehl | |||
<pre> | |||
solve(bvp,X)[1] | |||
</pre> | |||
lösen - das Ergebnis ist dann | |||
::<math> | |||
C_{I,0}=0, C_{I,1}=0, C_{I,2}=-q_0 a^2/4, C_{I,3}=3q_0 a/8, C_{II,0}=0, C_{II,1}=q_0 a^3/4, C_{II,2}=q_0 a^2/2, C_{II,3} =-q_0 a | |||
</math> | |||
Das gleiche passiert in der Matlab-Funktion linsolve in der solveAB.m: | |||
<pre> | |||
function x = solveAb(sys) | |||
% solve | |||
% linear system of equations A*x = b | |||
A = sys.sysmat(); | |||
b = sys.rhs(); | |||
x = linsolve(A,b); | |||
end | |||
</pre> | |||
Wir erhalten die Lösung | |||
<pre> | |||
X = | |||
1.0e+03 * | |||
0 | |||
0 | |||
-0.5000 | |||
0.7500 | |||
0 | |||
0.5000 | |||
1.0000 | |||
-2.0000 | |||
</pre> | |||
<math></math> | |||
<math></math> | |||
=== Post-Processing === | |||
Mit der algebraischen Lösung tragen wir <math>w(x)/w_{ref}</math> auf und finden | |||
[[Datei:MaMa-22.png|250px|left|mini|Dimensionslose Auslenkung aus der algebraischen Lösung mit Maxima.]] | |||
Die gleiche Lösung- und zusätzliche Graphen - kommen aus der numerischen Lösung mit Matlab: | |||
[[Datei:MaMa-21.png|300px|left|mini|Dimensionslose Auslenkung aus der numerischen Lösung mit Maxima.]] | |||
Die Lösungen stimmen - natürlich - überein. | |||
In Fällen, bei denen das lineare Gleichungssystem so wenige Unbekannte wie hier hat, würde man also die Lösung direkt in Maxima ermitteln. Wenn es komplizierter wird, muss man oft in die Numerik gehen, um in endlicher Zeit eine Lösung zu bekommen. | |||
<hr/> | <hr/> | ||
'''Links''' | '''Links''' | ||
* ... | * ... | ||
Aktuelle Version vom 15. Oktober 2024, 09:43 Uhr
Aufgabenstellung
Ein Stab der Länge und Biegesteifigkeit ist links fest eingespannt und wird bei 2/3 seiner Länger durch ein gelenkiges Lager gestützt. Zwischen dem freien rechten Rand und dem gelenkigen Lager wirkt eine konstante Streckenlast .
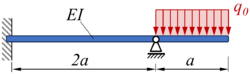
Gesucht ist die analytische Lösung für den Euler-Bernoulli-Balken und die Verläufe der Schnittgrößen. Im Vordergrund der Ausarbeitung steht das Zusammenspiel von Maxima (Computeralgebra) und Matlab (Numerik) zum Aufstellen, Verwalten und Lösen des linearen Gleichungssystems.
Die Aufgabe ist einfach genug, um sie analytisch mit Maxima allein zu lösen. Hier geht es aber darum, die "Zusammenarbeit" zwischen den beiden Software-Paketen exemplarisch vorzustellen. Dieses Zusammenspiel wird dann interessant, wenn die Anzahl der Gleichungen groß wird - typischer weise > 50. Dann ist eine algebraische Lösung oft nicht mehr praktikabel. Maxima eignet sich dann hervorragend für das Aufstellen und Verwalten der Gleichungen. Die konsolidierten Gleichungen werden dann zur numerischen Lösung an Matlab übergeben.
Wie das geht, zeigen wir hier.
Lösung mit Maxima und Matlab
Im folgenden finden Sie die Skripte für Maxima und Matlab, mit denen diese Aufgabe bearbeitet wurde.
Declarations
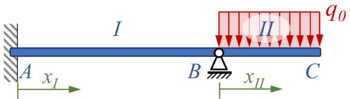
Wir zeichnen zunächst die Bereiche, Knoten und Koordinaten aus:
Für Bereich (zwischen und ) führen wir die unabhängige Koordinate ein, für Bereich (zwischen und ) die Koordinate .
Die zwei Bereiche haben die Längen
- und
- .
Um die gesuchte Lösung dimensionslos ansetzten zu können, wählen wir eine Vergleichslösung. Hier bietet sich der Kragbalken unter Streckenlast an. Diese liefert für die maximale Auslenkung von und die maximlae Kippung der Querschnitte von
- und
Unsere Lösung für teilen wir dann durch - und erhalten eine Aussage darüber, wie groß die Auslenkung unseres Systems im Vergleich zur Referenz-Auslenkung ist. Und dieses Verhältnis ist eine Zahl - ohne Parameter - so dass wir sie einfach interpretieren können.
Zusätzlich wählen wir
- und
für die Ergebnisse von und .
Boundary Value Problem
Das Randwertproblem wird im Feld von der Euler-Bernoulli-Differentialgleichung des Balkens und an den Rändern durch kinematische oder Kraft-Randbedingungen beschrieben.
Differentialgleichung des Euler-Bernoulli-Balkens
Die Gleichgewichtsbedingung am Balken führt auf die Differentialgleichung
Deren allgemeine Lösung (also ohne Anpassung an Rand- und Übergangsbedingungen) ist
| ... für die Auslenkung des Querschnitts: |
mit den 4 Integrationskonstanten - und damit unseren Unbekannten je Abschnitt -
- .
Aus Gleichgewichts- und Kinematik-Beziehungen kommen dann die weiteren Gleichungen
| ... für den Kippwinkel des Querschnitts: | |
| ... für das Biegemoment: | und |
| ... für die Querkraft: | . |
In unserer Aufgabe haben wir zwei Bereiche: in B müssen wir diese allgemeinen Lösungen aneinander anstückeln. Um sie zu unterscheiden, hängen wir für jede Lösung den Index des Bereichs an, also
| Bereich I |
Bereich II |
|---|---|
|
|
Und das gilt in gleicher Weise für die Gleichungen von .
Rand- und Übergangsbedingungen
Die Rand- und Übergangsbedingungen im Stab finden wir entweder aus kinematischen Überlegungen oder aus Gleichgewichtsbeziehungen mit den Schnittkräften des Balkens.
Kinematische Rand- und Übergangsbedingungen
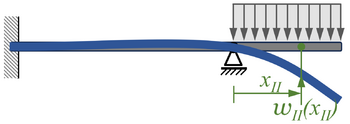
Für die Kinematik des Systems schauen wir uns die angenommene Verformung des Systems an:
Aus dem Bild entnehmen wir, dass
gilt.
Kraft- und Momenten Rand- und Übergangsbedingungen
Für die Übergangsbedingungen in B brauchen wir ein Freikörperbild:
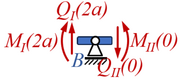
Die Gleichgewichtsbeziehungen erhalten wir dann zu
- ... in B:
- und
- ... in C (freier Rand):
Dies sind insgesamt 5+3=8 Rand- bzw. Übergangsbedingungen für die 8 Integrationskonstanten
- .
Konsolidierung der Gleichungen
Jetzt kommt Maxima ins Spiel.
Maxima-Quellcode
Im Quellcode für Maxima werden die Elemente aus dem Lösungsprozess oben direkt umgesetzt. So finden sich in "fcts" die Funktionen für .
Diese Funktionen können wir mit Maxima direkt in den Randbedingungen ansprechen und erhalten die Gleichungen
Diese Gleichungen kann man einzeln mit passenden Faktoren - z.B. - durchmultiplizieren und man erhält das einfacher aussehende lineare Gleichungssystem
Maxima hilft auch dabei, die von Null verschiedenen Elemente herauszusortieren und für Matlab zu formatieren für :
A( 1 , 1 ) = 1; A( 2 , 2 ) = 1; A( 3 , 1 ) = 1; A( 3 , 2 ) = 2*a; A( 3 , 3 ) = 2*a^2; A( 3 , 4 ) = (4*a^3)/3; A( 4 , 2 ) = 1; A( 4 , 3 ) = 2*a; A( 4 , 4 ) = 2*a^2; A( 4 , 6 ) = -1; A( 5 , 3 ) = -1; A( 5 , 4 ) = -(2*a); A( 5 , 7 ) = 1; A( 6 , 5 ) = 1; A( 7 , 7 ) = -1; A( 7 , 8 ) = -a; A( 8 , 8 ) = -1;
und :
b(7,1) = q0*a^2/2; b(8,1) = q0*a;
/*+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++*/
/* Modul Numerische Methoden der Mechanik */
/* Script zum Unterricht */
/* Löst: Gross e.a., Technische Mechanik, Bd 2, A 3.16 */
/* Autor: Andreas Baumgart */
/* Last Updated: 2024-11-13 */
/*+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++*/
/* parameters */
params: [ℓ[1]=2*a, ℓ[2]=a, q[1,0]=0];
/* reference-values */
refs: [w[ref]=q[2,0]*a^4/8/EI,
φ[ref]=q[2,0]*a^3/6/EI,
M[ref]=q[2,0]*a^2/2,
Q[ref]=q[2,0]*a];
/*****************************************/
/* the differential equation for the EBB */
ebb: [EI*diff(w[i](x),x,4)=0, w[i](x) = 1/EI*(q[i,0]*x^4/24+sum(1/j!*C[i,j]*x^j,j,0,3))];
/* ... and its solution */
fcts: [w[i](x) = diff(subst(ebb,w[i](x)),x,0),
φ[i](x) = diff(subst(ebb,w[i](x)),x,1),
M[i](x) =-EI*diff(subst(ebb,w[i](x)),x,2),
Q[i](x) =-EI*diff(subst(ebb,w[i](x)),x,3)];
/* boundary conditions */
bvp: [subst([i=1,x= 0 ], subst(fcts,w[i](x))) = 0,
subst([i=1,x= 0 ], subst(fcts,φ[i](x))) = 0,
subst([i=1,x=ℓ[1]], subst(fcts,w[i](x))) = 0,
subst([i=1,x=ℓ[1]], subst(fcts,φ[i](x))) = subst([i=2,x= 0 ], subst(fcts,φ[i](x))),
subst([i=1,x=ℓ[1]], subst(fcts,M[i](x))) = subst([i=2,x= 0 ], subst(fcts,M[i](x))),
subst([i=2,x= 0 ], subst(fcts,w[i](x))) = 0,
subst([i=2,x=ℓ[2]], subst(fcts,M[i](x))) = 0,
subst([i=2,x=ℓ[2]], subst(fcts,Q[i](x))) = 0];
X: flatten(makelist(makelist(C[i,j],j,0,3),i,1,2));
/* scale equations - so they look nicer ... */
scale: [EI,EI,EI,EI,1,EI,1,1];
for i:1 thru length(bvp) do
bvp[i]: subst(params,bvp[i])*scale[i];
/* preprocess */
bvp: expand(subst(refs,subst(params,bvp)));
ACM: augcoefmatrix(bvp,X);
A: submatrix(ACM,9);
b:-col(ACM,9);
print(A,"*",transpose(X),"=",b)$
/* you'll need to transfere these coefficients to Matlab: */
for row:1 thru 8 do
for col:1 thru 8 do
if notequal(subst(a=1,A[row][col]), 0) then
print("A(",row,",",col,") = ", A[row][col])$
/* Output for Matlab .....
A( 1 , 1 ) = 1;
A( 2 , 2 ) = 1;
A( 3 , 1 ) = 1;
A( 3 , 2 ) = 2*obj.a;
A( 3 , 3 ) = 2*obj.a^2;
A( 3 , 4 ) = (4*obj.a^3)/3;
A( 4 , 2 ) = 1;
A( 4 , 3 ) = 2*obj.a;
A( 4 , 4 ) = 2*obj.a^2;
A( 4 , 6 ) = -1;
A( 5 , 3 ) = -1;
A( 5 , 4 ) = -(2*obj.a);
A( 5 , 7 ) = 1;
A( 6 , 5 ) = 1;
A( 7 , 7 ) = -1;
A( 7 , 8 ) = -obj.a;
A( 8 , 8 ) = -1;
*/
/* solve */
/* we could also solve in Maxima : */
sol: solve(bvp,X)[1];
/* postprocess - an example: */
toPlot: expand(subst([x=ξ*a],subst(refs,subst(params,subst(sol,makelist(subst([i=j],subst(fcts, w[i](x)/w[ref])),j,1,2))))));
/* plot dimensionless displacements of beams in secsions I und II */
print("reference displacement w[ref] = ", subst(refs,w[ref]))$
plot2d([[parametric,ξ,toPlot[1],[ξ,0,2]],[parametric,2+ξ,toPlot[2],[ξ,0,1]]],[xlabel,"x/a->"],[ylabel,"w/w[ref]->"], [legend, "w_1", "w_2"]);
/* these are the functions needed in postprocessing in Matlab : */
for k:1 thru 4 do
(print(" for ", lhs(fcts[k])/lhs(refs[k]),":"),
print(expand(subst([x=ξ*a],subst(params,makelist(subst([i=j],subst(refs,subst(fcts, lhs(fcts[k])/lhs(refs[k])))),j,1,2))))))$
/* note that x=xi*a has been introduced as the dimensionless coordinate */
Matlab©-Quellcode
Genau so wird der Code dann in Matlab eingefügt - hier mit der Änderung, dass und Properties der EBB-Class sind und entsprechend innerhalb der Klasse als obj.a bzw obj.q angesprochen werden müssen, also
:
:
function A = sysmat(obj)
%populate
% system matrix A
% create matrix
A = zeros(8,8);
% populate matrix (only non-zero elements)
A( 1 , 1 ) = 1;
A( 2 , 2 ) = 1;
A( 3 , 1 ) = 1;
A( 3 , 2 ) = 2*obj.a;
A( 3 , 3 ) = 2*obj.a^2;
A( 3 , 4 ) = (4*obj.a^3)/3;
A( 4 , 2 ) = 1;
A( 4 , 3 ) = 2*obj.a;
A( 4 , 4 ) = 2*obj.a^2;
A( 4 , 6 ) = -1;
A( 5 , 3 ) = -1;
A( 5 , 4 ) = -(2*obj.a);
A( 5 , 7 ) = 1;
A( 6 , 5 ) = 1;
A( 7 , 7 ) = -1;
A( 7 , 8 ) = -obj.a;
A( 8 , 8 ) = -1;
end
function b = rhs(obj)
%populate
% right-hand side
% cretae matrix
b = zeros(8,1);
% populate matrix
b(7,1) = obj.q*obj.a^2/2;
b(8,1) = obj.q*obj.a;
end
:
:
Die Datei-Struktur links zeigt das Skript MaMa.m sowie Classes und Functions in den jeweiligen Ordnern. Die Excel-Datei enthält alle System-Parameter.
Den komplette Quellcode zu diesem Programm können Sie über dieses ZIP-File rechts herunterladen.

download compressed archive →
Solving
Die Gleichungen lösen wir in Maxima mit dem Befehl
solve(bvp,X)[1]
lösen - das Ergebnis ist dann
Das gleiche passiert in der Matlab-Funktion linsolve in der solveAB.m:
function x = solveAb(sys) % solve % linear system of equations A*x = b A = sys.sysmat(); b = sys.rhs(); x = linsolve(A,b); end
Wir erhalten die Lösung
X =
1.0e+03 *
0
0
-0.5000
0.7500
0
0.5000
1.0000
-2.0000
Post-Processing
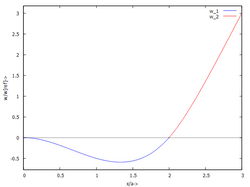
Mit der algebraischen Lösung tragen wir auf und finden
Die gleiche Lösung- und zusätzliche Graphen - kommen aus der numerischen Lösung mit Matlab:
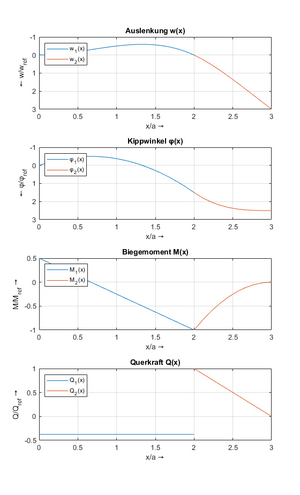
Die Lösungen stimmen - natürlich - überein. In Fällen, bei denen das lineare Gleichungssystem so wenige Unbekannte wie hier hat, würde man also die Lösung direkt in Maxima ermitteln. Wenn es komplizierter wird, muss man oft in die Numerik gehen, um in endlicher Zeit eine Lösung zu bekommen.
Links
- ...
