Werkzeuge/Gleichgewichtsbedingungen/Arbeitsprinzipe der Analytischen Mechanik/Prinzip der virtuellen Verrückungen: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
KKeine Bearbeitungszusammenfassung |
||
| (10 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
Das Prinzip der virtuellen Verrückungen und das Prinzip der virtuellen Kräfte gehören zum Prinzip der virtuellen Arbeit. Wie alle Gleichgewichtsprinzipe der Analytische Mechanik ist der Ausgangspunkt auch hier die Überlegung, dass Energie in einem abgeschlossenen System erhalten bleibt - und sich daraus mathematische Formulierungen zu Gleichgewichtsbedingungen ableiten lassen.Das Prinzip der virtuellen Verrückungen spielt dabei in kommerziellen Anwendungen die wichtigere Rolle der beiden. Der sperrige Begriff "Verrückung" sollte Sie dabei nicht abschrecken: er steht für Verschiebung und Verdrehung, also für translatorische und rotatorische Bewegung.Ausgangspunkt dieses Prinzips ist der | Das Prinzip der virtuellen Verrückungen und das [[Sources/Lexikon/Prinzip der virtuellen Kräfte|Prinzip der virtuellen Kräfte]] gehören zum [[Sources/Lexikon/Prinzip der virtuellen Arbeit|Prinzip der virtuellen Arbeit]]. Wie alle Gleichgewichtsprinzipe der [[Sources/Lexikon/Analytische Mechanik|Analytische Mechanik]] ist der Ausgangspunkt auch hier die Überlegung, dass Energie in einem abgeschlossenen System erhalten bleibt - und sich daraus mathematische Formulierungen zu Gleichgewichtsbedingungen ableiten lassen.Das Prinzip der virtuellen Verrückungen spielt dabei in kommerziellen Anwendungen die wichtigere Rolle der beiden. Der sperrige Begriff "Verrückung" sollte Sie dabei nicht abschrecken: er steht für Verschiebung und Verdrehung, also für translatorische und rotatorische Bewegung.Ausgangspunkt dieses Prinzips ist der [[Sources/Lexikon/Arbeit|Arbeit]]sbegriff, hier setzen wir die kleine Verschiebung ''Δr'' zur virtuellen Verschiebung ''δr:'' | ||
::<math>\Delta W := \Delta \vec{r} \cdot \vec{F} \longrightarrow \delta W := \delta \vec{r} \cdot \vec{F}</math> | |||
::<math>\Delta W := \Delta \vec{r} \cdot \vec{F} \longrightarrow \delta W := \delta \vec{r} \cdot \vec{F}</math> | |||
[[Datei:PrinzipDerVirtuellenVerrückungen-Definition.png|left|mini|150px|Virtuelle Arbeit einer Kraft.]] | |||
Für '''starre''' Systeme fordert das Prinzip, dass die Summe aller virtuellen Arbeiten ''δW<sup>a</sup>'' äußerer, eingeprägter Lasten - also die Arbeit der Kräfte am System im Gleichgewicht auf den virtuellen Verrückungen - verschwinden: | Für '''starre''' Systeme fordert das Prinzip, dass die Summe aller virtuellen Arbeiten ''δW<sup>a</sup>'' äußerer, eingeprägter Lasten - also die Arbeit der Kräfte am System im Gleichgewicht auf den virtuellen Verrückungen - verschwinden: | ||
| Zeile 11: | Zeile 12: | ||
::<math>\begin{array}{ll}\delta W & = \delta W^a - \delta \Pi\\&\stackrel{!}{=}0\end{array}</math>(vgl. PvV2) | ::<math>\begin{array}{ll}\delta W & = \delta W^a - \delta \Pi\\&\stackrel{!}{=}0\end{array}</math>(vgl. PvV2) | ||
Das beste an Arbeitsprinzipen: die Gleichgewichtsbeziehung leiten wir aus skalaren Größen ab. Die Anteile von beliebig komplexen Systemen ergeben sich einfach aus der '''Summe''' der ''i'' Teilsysteme | |||
::<math>\displaystyle \delta W^a = \sum_i W^a_i, \;\;\;\delta \Pi = \sum_i \Pi_i</math>. | |||
Dabei ist | Dabei ist | ||
| Zeile 16: | Zeile 21: | ||
::<math>\delta\Pi = \displaystyle \int_{V} \underline{\sigma} \cdot \delta\underline{\varepsilon}\; dx</math>. | ::<math>\delta\Pi = \displaystyle \int_{V} \underline{\sigma} \cdot \delta\underline{\varepsilon}\; dx</math>. | ||
Meist bieten die Struktur-Modelle - wie Dehnstab, Euler-Bernoulli-Balken oder Schale - die Möglichkeit, das Integrale über | Meist bieten die Struktur-Modelle - wie [[Sources/Lexikon/Dehnstab|Dehnstab]], [[Sources/Lexikon/Euler-Bernoulli-Balken|Euler-Bernoulli-Balken]] oder [[Sources/Lexikon/Schale|Schale]] - die Möglichkeit, das Integrale über | ||
* Skalarprodukt von Spannungen im Bauteil und | * Skalarprodukt von Spannungen im Bauteil und | ||
| Zeile 34: | Zeile 39: | ||
'''Video:''' | '''Video:''' | ||
* ABR0 (Prinzip der virtuellen Verrückungen) | * [[Sources/Lernvideos/ABR0|ABR0]] (Prinzip der virtuellen Verrückungen) | ||
'''Links:''' | '''Links:''' | ||
{{Category:Prinzip_der_virtuellen_Verrückungen}} | #{{Category:Prinzip_der_virtuellen_Verrückungen}} | ||
#[[Sources/Lexikon/Virtuelle_Verrückung|Virtuelle_Verrückung]] | |||
Aktuelle Version vom 30. März 2022, 05:12 Uhr
Das Prinzip der virtuellen Verrückungen und das Prinzip der virtuellen Kräfte gehören zum Prinzip der virtuellen Arbeit. Wie alle Gleichgewichtsprinzipe der Analytische Mechanik ist der Ausgangspunkt auch hier die Überlegung, dass Energie in einem abgeschlossenen System erhalten bleibt - und sich daraus mathematische Formulierungen zu Gleichgewichtsbedingungen ableiten lassen.Das Prinzip der virtuellen Verrückungen spielt dabei in kommerziellen Anwendungen die wichtigere Rolle der beiden. Der sperrige Begriff "Verrückung" sollte Sie dabei nicht abschrecken: er steht für Verschiebung und Verdrehung, also für translatorische und rotatorische Bewegung.Ausgangspunkt dieses Prinzips ist der Arbeitsbegriff, hier setzen wir die kleine Verschiebung Δr zur virtuellen Verschiebung δr:
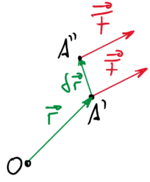
Für starre Systeme fordert das Prinzip, dass die Summe aller virtuellen Arbeiten δWa äußerer, eingeprägter Lasten - also die Arbeit der Kräfte am System im Gleichgewicht auf den virtuellen Verrückungen - verschwinden:
- (vgl. PvV1).
Für elastische Systeme dagegen muss die Differenz aus δWa und der virtuellen Formänderungsenergie δΠ verschwinden.
- (vgl. PvV2)
Das beste an Arbeitsprinzipen: die Gleichgewichtsbeziehung leiten wir aus skalaren Größen ab. Die Anteile von beliebig komplexen Systemen ergeben sich einfach aus der Summe der i Teilsysteme
- .
Dabei ist
- .
Meist bieten die Struktur-Modelle - wie Dehnstab, Euler-Bernoulli-Balken oder Schale - die Möglichkeit, das Integrale über
- Skalarprodukt von Spannungen im Bauteil und
- den Verzerrungen durch dem virtuellen Verschiebungszustand
teilweise über das Volumen auszuwerten. Zum Beispiel finden wir für den Euler-Bernoulli-Balken
Das Prinzip fordert, dass die virtuellen Verrückungen diese Eigenschaften erfüllen:
- sie sind gedachte, voneinander unabhängige Verschiebungen (also in Wirklichkeit nicht unbedingt eintretende Verschiebungen), aber
- sie sind mit der geometrischen Konfiguration des Systems verträglich (an einem festen Gelenklager verschwinden die virtuellen Verschiebungen) und
- sie sind differentiell klein.
Alle drei geforderten Eigenschaften erscheinen nicht unmittelbar sinnvoll - bitte haben Sie etwas Geduld.
Video:
- ABR0 (Prinzip der virtuellen Verrückungen)
Links: