Sources/Lexikon/Axiome der Statik: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| (4 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{| class="wikitable" | {| class="wikitable" | ||
| Zeile 7: | Zeile 6: | ||
| | | | ||
=== Axiom 1: === | === Axiom 1: === | ||
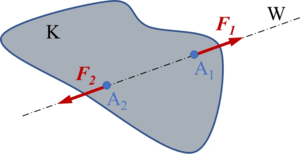
Ein freier, starrer Körper Κ ist unter der Wirkung von zwei Kräften | Ein freier, starrer Körper Κ ist unter der Wirkung von zwei Kräften <math display="inline">\vec{F}_1</math>, <math display="inline">\vec{F}_2</math> dann und nur dann im Gleichgewicht, wenn sie in die Verbindungslinie ihrer beiden Angriffspunkte ''A<sub>1</sub>'', ''A<sub>2</sub>'' fallen, entgegengesetzt orientiert und gleich groß sind. | ||
{| class="wikitable" | {| class="wikitable" | ||
|[[Datei:AxiomeDerStatik-A1.png|mini|Bild A1-1: Körper im Gleichgewicht]] | |[[Datei:AxiomeDerStatik-A1.png|mini|Bild A1-1: Körper im Gleichgewicht]] | ||
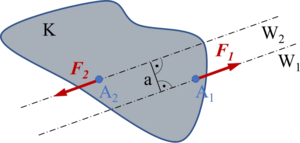
|[[Datei:AxiomeDerStatik-1-b.png|mini|Bild A1-2: Körper nicht im Gleichgewicht]] | |[[Datei:AxiomeDerStatik-1-b.png|mini|Bild A1-2: Körper nicht im Gleichgewicht]] | ||
|} | |} | ||
Formal bedeutet dies zweierlei (vgl. Bilder A1-1 und -2): Die Vektorsumme aus | Formal bedeutet dies zweierlei (vgl. Bilder A1-1 und -2): Die Vektorsumme aus <math display="inline">\vec{F}_1</math>, <math display="inline">\vec{F}_2</math> und der Abstand ''a'' müssen verschwinden. | ||
Durch die erste Gleichung wird der Teil des Axioms „entgegengesetzt orientiert und gleich groß" erfasst, erst mit ''a'' = 0 werden die Kräfte auch in die Verbindungslinie der beiden Angriffspunkte gezwungen. | Durch die erste Gleichung wird der Teil des Axioms „entgegengesetzt orientiert und gleich groß" erfasst, erst mit ''a'' = 0 werden die Kräfte auch in die Verbindungslinie der beiden Angriffspunkte gezwungen. | ||
| Zeile 26: | Zeile 25: | ||
| | | | ||
===Axiom 2:=== | ===Axiom 2:=== | ||
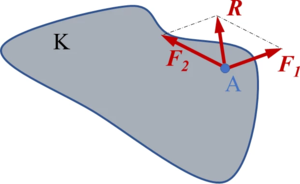
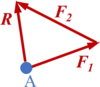
Greifen zwei | Greifen zwei Kräfte <math display="inline">\vec{F}_1</math> und <math display="inline">\vec{F}_2</math> an einem gemeinsamen Angriffspunkt A an, so können sie durch eine Kraft <math display="inline">\vec{R}</math> ersetzt werden, die sich als die Diagonale des durch die beiden Kräfte aufgespannten Parallelogramms ergibt, Bild 3. | ||
Gemäß Bild 3, ist die Diagonale R die (geometrische) Summe der beiden | Gemäß Bild 3, ist die Diagonale <math display="inline">\vec{R}</math> die (geometrische) Summe der beiden Vektoren <math display="inline">\vec{F}_1</math> und <math display="inline">\vec{F}_2</math> : | ||
::<math>\vec{R} = \vec{F}_1+\vec{F}_2</math>. | ::<math>\vec{R} = \vec{F}_1+\vec{F}_2</math>. | ||
| Zeile 43: | Zeile 42: | ||
'''Definition:''' Gemäß dem Kräfteparallelogramm in Bild führt man <math display="inline">\vec{R}</math> als resultierende Kraft - kurz Resultierende - der beiden (Einzel-)Kräfte <math display="inline">\vec{F}_1</math> und <math display="inline">\vec{F}_2</math> ein. Die Resultierende ersetzt die (Wirkung der) Einzelkräfte! | '''Definition:''' Gemäß dem Kräfteparallelogramm in Bild führt man <math display="inline">\vec{R}</math> als resultierende Kraft - kurz Resultierende - der beiden (Einzel-)Kräfte <math display="inline">\vec{F}_1</math> und <math display="inline">\vec{F}_2</math> ein. Die Resultierende ersetzt die (Wirkung der) Einzelkräfte! | ||
{{MyNote|title= | {{MyNote|title=Hinweis 1|text=Bildet man die Resultierende für zwei Kräfte in einem Lageplan oder Schnittbild, so muß man mit dem Kräfteparallelogramm und darf nicht mit dem Krafteck arbeiten.}} | ||
{{MyNote|title= | {{MyNote|title=Hinweis 2|text=Man kann auch die Wirkung einer (resultierenden) Kraft <math display="inline">\vec{R}</math> gemäß Kräfteparallelogramm (Bild) durch die Wirkung der beiden Kräfte <math display="inline">\vec{F}_1</math> und <math display="inline">\vec{F}_2</math> ersetzen. dann heißen <math display="inline">\vec{F}_1</math> und <math display="inline">\vec{F}_2</math> Komponenten von <math display="inline">\vec{R}</math>.}} | ||
{{MyNote|title= | {{MyNote|title=Hinweis 3|text=Die erste Gleichung von Axiom 1 kann man nun als <math display="inline">\vec{F}_1</math> und <math display="inline">\vec{F}_2</math> = <math display="inline">\vec{R}</math> und <math display="inline">\vec{R}</math> = <math display="inline">\vec{0}</math> interpretieren. Notwendig für das Gleichgewicht des in Bild A2-1 gezeigten Körpers ist es, daß die Resultierende der beiden Kräfte <math display="inline">\vec{F}_1</math> und <math display="inline">\vec{F}_2</math> verschwindet.}} | ||
|} | |} | ||
Aktuelle Version vom 17. Februar 2021, 14:35 Uhr
| Kräfte-Parallelogramm | |||||||||
|---|---|---|---|---|---|---|---|---|---|
Axiom 2:Greifen zwei Kräfte und an einem gemeinsamen Angriffspunkt A an, so können sie durch eine Kraft ersetzt werden, die sich als die Diagonale des durch die beiden Kräfte aufgespannten Parallelogramms ergibt, Bild 3. Gemäß Bild 3, ist die Diagonale die (geometrische) Summe der beiden Vektoren und :
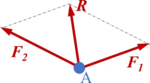
Das Kräfteparallelogramm (Bild 3) enthält den Angriffspunkt A, im Kräftedreieck (Krafteck, Kräfteplan) bleibt der Angriffspunkt unberücksichtigt (vgl. Bild).
Definition: Gemäß dem Kräfteparallelogramm in Bild führt man als resultierende Kraft - kurz Resultierende - der beiden (Einzel-)Kräfte und ein. Die Resultierende ersetzt die (Wirkung der) Einzelkräfte!
|
| Hinzufügen oder Wegnehmen einer Gleichgewichtsgruppe | ||
|---|---|---|
| Definition: Eine Gruppe von zwei oder mehr Kräften, die sich - allein auf einen freien, starren Körper Κ wirkend - im Gleichgewicht hält, heißt Gleichgewichtsgruppe.
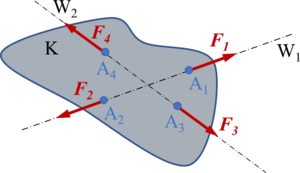
Beispiel: Die beiden Kräfte aus Axiom 1. Axiom 3:Befindet sich ein freier, starrer Körper Κ (unter der Wirkung von irgendwelchen Kräften) im Gleichgewicht, so bleibt er im Gleichgewicht, wenn eine Gleichgewichtsgruppe hinzugefügt oder weggenommen wird. In dem als Beispiel skizzierten System von Bild A3-1 sei der Körper Κ unter der Wirkung der Kräfte , im Gleichgewicht (vgl. Axiom 1). Die hinzugefügte Gleichgewichtsgruppe , die ihrerseits Axiom 1 genügt, ändert den Gleichgewichtszustand des Körpers Κ nicht!
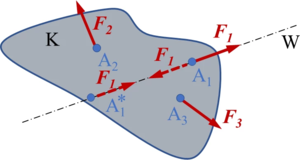
So sei der in Bild A3-2 gezeigte Körper unter der Wirkung der Kräfte , , im Gleichgewicht. Wir legen die Gleichgewichtsgruppe , (in Bild A3-2 gestrichelt) so auf den Körper, dass , bei A1 und im Punkt A* angreift. Dann heben sich die bei A1 angreifenden Kräfte auf (ihre Resultierende verschwindet), wir erhalten die „längs der Wirkungslinie W nach A1 verschobene Kraft ." |
| Übertragen einer Gleichgewichtsgruppe auf einen anderen Körper |
|---|
Axiom 4:Ist ein freier, starrer Körper K1 unter einer gegebenen Gruppe von Kräften im Gleichgewicht, so ist auch der freie, starre Körper K2 unter der Wirkung dieser Kräfte (allein) im Gleichgewicht. Nutzen: Man kann den Gleichgewichtszustand an dem der Anschauung am besten zugänglichen Körper überprüfen. |
| Befreiungsprinzip von Lagrange |
|---|
Axiom 5:Das Gleichgewicht eines nicht freien, starren Körpers ändert sich nicht, wenn man ihn von den (Ver-)Bindungen mit seiner Umgebung befreit - ihn freischneidet falls man nur die Bindungen durch die von ihnen ausgeübten Kräfte (= Kraftpfeile) ersetzt. (Dies ist eine Erweiterung des Eulerschen Schnittprinzips). Die Frage nach den Bindungstypen und den von ihnen übertragenen Kräften wird an einfachsten Beispielen in den folgenden Überlegungen zum Reaktionsprinzip und zu den Kräften auf glatte Körper behandelt. |
| Reaktionsprinzip | ||
|---|---|---|
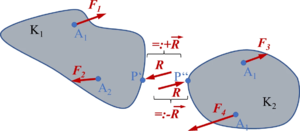
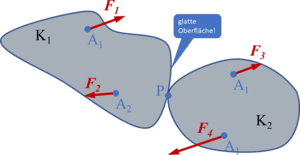
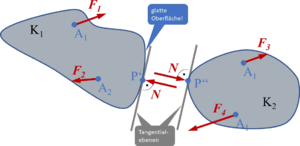
Axiom 6:Seien in Bild A6-1 die beiden Körper K1 und K2 zunächst miteinander (am Punkt P) verbunden. Durch einen Schnitt (Axiom 5) werden sie voneinander befreit (Bild A6-2). Der Körper K2 übe auf den Körper K1 die Kraft aus; dann übt der Körper K1 auf den Körper K2 die Kraft aus. Die Kräfte haben gleiche Größe und Richtung, doch entgegengesetzte Orientierung; in Skizzen werden sie durch gleiche Maßzahlen F und entgegengesetzt orientierte Pfeile gekennzeichnet. Man spricht kurz von der Reaktionskraft ; die Bedeutung - welche Kraft man mit und welche mit meint - entnimmt man den Skizzen.
|
| Kräfte auf glatte Körper | ||
|---|---|---|
Axiom 7:Definition: Greift eine Kraft an einem Punkt Ρ eines Körpers „von außen" an und steht sie senkrecht auf der Tangentialebene an den Körper in diesem Punkt (s. Bild A7-2), so kennzeichnen wir dies durch die Benennung Normalkraft und die Bezeichnung Definition: Greift eine Kraft an einem Punkt Ρ eines Körpers „von außen" an und steht sie senkrecht auf der Tangentialebene an den Körper in diesem Punkt (s. Bild A7-2), so kennzeichnen wir dies durch die Benennung Normalkraft und die Bezeichnung . Berühren sich zwei glatte Körper (s. Bild A7-1), so steht eine Reaktionskraft senkrecht auf der gemeinsamen Tangentialebene und ist ins Innere der Körper gerichtet (s. Bild A7-2). Es gilt > 0 (bei < 0 würden die Körper voneinander abheben).
|
| Das Erstarrungsprinzip |
|---|
Axiom 8:Ein freier, nicht starrer Körper ist genau dann im Gleichgewicht,wenn er als starrer Körper im Gleichgewicht wäre. Anschauliche Deutung: Wenn man sich einen Körper momentan „eingefroren" vorstellt, ändert sich das Gleichgewicht nicht. |
| Systeme von Körpern |
|---|
Axiom 9:Ein System von Körpern ist genau dann im Gleichgewicht, wenn alle Einzelkörper im Gleichgewicht sind. (Man beachte die Verbindung zum Befreiungsprinzip, Axiom 5.) |
| Bewegte Körper |
|---|
|
Definition: Man sagt, ein Körper sei masselos, wenn man die aus seiner (beschleunigten) Bewegung herrührenden (Massen-Trägheits-)Kräfte gegenüber den anderen auftretenden Kräften vernachlässigen kann Axiom 10:Ein bewegter, freier, starrer, masseloser Körper ist genau dann im Gleichgewicht, wenn er von einem mit ihm mitgeführten Bezugssystem aus gesehen in jedem Augenblick im „statischen Gleichgewicht" ist. |