Gelöste Aufgaben/T3BP: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| (20 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 8: | Zeile 8: | ||
==Aufgabenstellung== | ==Aufgabenstellung== | ||
<onlyinclude> | <onlyinclude> | ||
Wir untersuchen das „Three-Body-Problem“(vgl. [https://en.wikipedia.org/wiki/Three-body_problem Wikipedia]) numerisch. Dabei sollen die Bahnen von drei Körper mit den Punktmassen <i>m<sub>1</sub>, m<sub>2</sub>, m<sub>3</sub></i> in Wechselwirkung miteinander berechnet werden. | |||
[[Datei:T3BP-01.png|150px|left|mini|"Die Drei Sonnen"]] | [[Datei:T3BP-01.png|150px|left|mini|"Die Drei Sonnen"]] | ||
Gesucht ist die Lösung des Anfangswertproblems für verschiedene Anfangswerte (Orte und Geschwindigkeiten) und Massen <i> | Gesucht ist die Lösung des Anfangswertproblems für verschiedene Anfangswerte (Orte und Geschwindigkeiten) und Massen <i>m<sub>i</sub></i> der Körper. | ||
</onlyinclude> | </onlyinclude> | ||
== Lösung mit Matlab® == | == Lösung mit Matlab® == | ||
Die Lösung mit Matlab erfordert keine großen algebraischen Vorbereitungen - für die wir sonst Maxima einsetzten würden. | |||
Als äußere Kräfte treten nur die Feldkräfte der Gravitation zwischen den Körpern auf - die wir einfach hinschreiben und in Matlab implementieren können. | |||
<!-------------------------------------------------------------------------------->{{MyCodeBlock|title=Declarations | <!-------------------------------------------------------------------------------->{{MyCodeBlock|title=Declarations | ||
|text= | |text=Dafür verwenden wir das script <code>T3BP.m</code>, das die Funktionen | ||
* <code>preprocess.m</code>, | |||
* <code>ode45.m</code> (solve) und | |||
* <code>postprocess.m</code> | |||
aufruft. Die Klasse | |||
* <code>planets.m</code> | |||
verwenden wir nur, um die Systemparameter "<code>sys</code>" bequem ansprechen zu können. | |||
Zur Lösung des Anfangswertproblems rufen wir eine der ODE-Funktionen aus Matlab auf, die wir mit den Gleichgewichtsbedingungen unserer Funktion <code>t3bpdydt.m</code> füttern. | |||
|code= | |code= | ||
<syntaxhighlight lang=" | <syntaxhighlight lang="notmuch" line start=1> | ||
T3BP | |||
|- preprocess | |||
|- class sys=planets(data) | |||
|- ode45 | |||
|- t3bpdydt | |||
|- postprocess | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
<!-------------------------------------------------------------------------------->{{MyCodeBlock|title=Equilibrium Conditions | <!-------------------------------------------------------------------------------->{{MyCodeBlock|title=Equilibrium Conditions | ||
|text= | |text=Die Gravitationskräfte zwischen den zwei Körpern <i>i</i> und <i>j</i> erfasst | ||
::<math>F_{i,j} = G \cdot \frac{\displaystyle m_i\cdot m_j}{\displaystyle r_{i,j}^2}</math> | |||
mit der [https://en.wikipedia.org/wiki/Gravitational_constant Gravitationskonstanten] | |||
::<math>G = 6.674\cdot 10^{-11} \frac{\displaystyle m^3}{\displaystyle kg \cdot s^2}.</math> | |||
Dabei gehen die Wirkungslinien der Kräfte durch die Massenmittelpunkte der Körper, die Körper ziehen sich gegenseitig an. | |||
Damit ist | |||
::<math>\vec{F}_{i,j} = F_{i,j} \cdot \vec{e}_{i,j}</math>, | |||
wobei <math>\vec{e}_{i,j}</math> der Einheitsvektor der Anziehungskraft - in diesem Fall von <i>i</i> nach <i>j</i> - ist. | |||
Die Bewegungsgleichungen schreiben wir mit <math>F</math> in Vektorschreibweise für Körper <i>i</i> als | |||
::<math> m_i \dot \ddot{\vec{u}}_i = \sum_{\ell=j,k} G\cdot \underbrace{\frac{\displaystyle m_i\cdot m_\ell}{\displaystyle r_{i,\ell}^2}}_{=F_{i,j}} \cdot \vec{e}_{i,\ell} \text{ mit } | |||
\vec{u}_i = \left(\vec{e}_x,\vec{e}_y,\vec{e}_z\right)\cdot \underbrace{\left(\begin{array}{l}u_x\\u_y\\u_z\end{array}\right)}_{\displaystyle = \underline{u}_i}</math>. | |||
Dabei ist z.B. <i>i=1</i> und <i><math>\ell</math>=2,3</i>. | |||
Die drei Bewegungsgleichungen in den drei räumlichen Koordinaten <i><u>u</u><sub>i</sub></i> formulieren wir in dimensionslosen Koordinaten. Dafür brauchen wir drei unabhängige Referenzgrößen, hier wählen wir | |||
::<math> | |||
\begin{array}{lcll} | |||
M&=&m_1&\text{ Referenz-Masse}\\ | |||
L&=&1.6 10^{11} \text{km}&\text{ Referenz-Länge: der Durchmesser unseres Sonnensystems und}\\ | |||
F&=& G\cdot \frac{\displaystyle m_1\cdot m_1}{\displaystyle L^2}& \text{ Referenz-Kraft} | |||
\end{array}. | |||
</math> | |||
Uns fehlt noch die Referent-Zeit <i>T</i>, die wir aus | |||
::<math> | |||
F = \frac{\displaystyle m_1\cdot L}{\displaystyle T^2} \text{ zu } T = \sqrt{\frac{\displaystyle m_1\cdot L}{\displaystyle F}} | |||
</math> | |||
erhalten. Damit ist <math>T \approx 175 Jahre</math>. | |||
Damit können wir schreiben: | |||
::<math> | |||
\begin{array}{lcll} | |||
t&=&\tau \cdot T&\text{ mit der dimensionslosen Zeit } \tau\\ | |||
m_i&=&\theta_i \cdot m_1&\text{ mit der dimensionslosen Masse } \theta_i\\ | |||
\underline{u}_i(t)&=&L\cdot \underline{U}_i(\tau)&\text{ mit den dimensionslose Koordinaten } U_i \text{ und}\\ | |||
r_{i,j}&=& L \cdot \varrho_{i,j}&\text{ mit dem dimensionslosen Abstand zweier Körper } \varrho_{i,j} | |||
\end{array}. | |||
</math> | |||
Einsetzen und Kürzen liefert uns dann die dimensionslosen Bewegungsgleichungen | |||
::<math> \ddot{\underline{U}}_i = \sum_{\ell=j,k} \frac{\displaystyle \theta_\ell}{\displaystyle \varrho_{i,\ell}^2} \cdot \underline{e}_{i,\ell} </math>. | |||
Diese Gleichgewichtsbeziehungen implementieren wir in der Funktion <code>t3bpdydt.m</code>, die vom Löser <code>ODE45</code> aufgerufen wird. | |||
|code= | |code= | ||
<syntaxhighlight lang=" | <syntaxhighlight lang="matlab" line start=1> | ||
1+1 | function dydt = t3bpdydt(t,y,sys) | ||
% implementation of ode | |||
% sys holds system parameters | |||
% get coordinates | |||
for body = 1:3 | |||
u(body,1:3) = transpose(y(3*(body-1)+1:3*body,1)); | |||
end | |||
r = zeros(3,3,3); | |||
e = zeros(3,3,3); | |||
% compose vectors, unit vectors and distances | |||
r(1,2,:) = u(2,:)-u(1,:); % this from m[1] to m[2] | |||
: | |||
: | |||
: | |||
% mass 3 | |||
dydt(9+7:9+9,1)=sys.theta(1)/R(3,1)*e(3,1,:)+sys.theta(2)/R(3,2)*e(3,2,:); | |||
%% velocities | |||
dydt(1:9,1) = y(10:18,1); | |||
%% | |||
waitbar(t / sys.tEnd); | |||
end | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
<!-------------------------------------------------------------------------------->{{MyCodeBlock|title=Solving | <!-------------------------------------------------------------------------------->{{MyCodeBlock|title=Solving | ||
|text= | |text=Die Lösung des Anfangswertproblems übertragen wir der Matlab-Routine ODE45. | ||
Dabei organisieren wir die Zustandsgrößen so, dass in <code>y0</code> zunächst die 9 Anfangsverschiebungen und dann die 9 Anfangsgeschwindigkeiten stehen. | |||
Wir lösen dann | |||
::<math>\dot{\underline{q}}(\tau) = \underline{f}(\underline{q}(\tau))</math> | |||
mit | |||
::<math>\underbrace{\underline{q}(0)}_{= \text{y0}} = \left(\begin{array}{c} | |||
U_{1,x}(0)\\ | |||
U_{1,y}(0)\\ | |||
U_{1,z}(0)\\ | |||
U_{2,x}(0)\\ | |||
\vdots\\ | |||
V_{3,y}(0)\\ | |||
V_{3,z}(0) | |||
\end{array}\right).</math> | |||
Die <math>V_{i,\xi}</math> sind Komponentenweise die Geschwindigkeiten, also z.B. | |||
::<math>V_{3,y}(\tau) = \frac{\displaystyle d}{\displaystyle d\tau} U_{3,y}(\tau)</math>. | |||
|code= | |code= | ||
<syntaxhighlight lang=" | <syntaxhighlight lang="matlab" line start=1> | ||
1 | %% solve IVP | ||
% set-up numerical paramters | |||
tspan = 0:sys.tEnd/1000:sys.tEnd; | |||
u0 = [transpose(sys.u0(1,:));transpose(sys.u0(2,:));transpose(sys.u0(3,:))]/sys.L; | |||
v0 = [transpose(sys.v0(1,:));transpose(sys.v0(2,:));transpose(sys.v0(3,:))]*sys.T/sys.L; | |||
% initial values from sys structured for ODE45 | |||
y0 = [u0;v0]; | |||
h = waitbar(0,'solving ODE - please wait...'); | |||
% | |||
[t,y] = ode45(@(t,y)t3bpdydt(t,y,sys),tspan,y0); | |||
close(h); | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
{{MyZipfileBlock | |||
|text= | |title=Matlab<sup>©</sup>-files | ||
|text =[[Datei:matlab-folder-structure.png|links|mini|Folder Structure]]Die Datei-Struktur des Projekts zeigt das Bild links mit dem Skript <nowiki>T3BP.m</nowiki>. Classes und Functions sind in den jeweiligen Ordnern. Die Excel-Datei hält alle System-Parameter. | |||
Den komplette Quellcode zu diesem Programm können Sie über dieses ZIP-File rechts herunterladen. | |||
|file =T3BP.zip}} | |||
[[Datei:T3BP- | <!-------------------------------------------------------------------------------->{{MyCodeBlock|title=Post-Processing | ||
|text=[[Datei:T3BP-21.png|550px|right|mini|Trajektoren der Körper]] | |||
Uns interessieren natürlich die Trajektorien der Körper im Raum - dabei zeichnen wir die Körper-Durchmesser entsprechend Ihrer Masse. Die Darstellung ist nicht maßstäblich. | |||
[[Datei:T3BP- | Zur Kontrolle können wir prüfen, ob die ODE-Routine im Rahmen der numerischen Genauigkeit die Erhaltungssätze der Mechanik erfüllt. Das machen wir hier am Beispiel des Impulssatzes: die Summe der Bewegungsgrößen jeweils in die drei Raumrichtungen muss gleich bleiben: | ||
[[Datei:T3BP-22.png|150px|left|mini|Bewegungsgrößen <math>\sum_{i=1}^3 \theta_i \cdot I_{i,x0}</math>]]. | |||
Und das tut sie offensichtlich auch - im Rahmen der numerischen Genauigkeit. | |||
Und schließlich schauen wir uns die Bewegung der drei Körper in einer Animation über der Zeit an - hier über einen Zeitraum 4375 Jahren. | |||
[[Datei:T3BP-23.mp4|100%|left|mini|Animation der Bewegung]] | |||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
nothing here | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
<hr/> | <hr/> | ||
'''Literature''' | '''Literature''' | ||
* .. | * [https://en.wikipedia.org/wiki/The_Three-Body_Problem_(novel) The Three-Body-Problem] | ||
Aktuelle Version vom 3. Oktober 2022, 20:43 Uhr
Aufgabenstellung
Wir untersuchen das „Three-Body-Problem“(vgl. Wikipedia) numerisch. Dabei sollen die Bahnen von drei Körper mit den Punktmassen m1, m2, m3 in Wechselwirkung miteinander berechnet werden.
Gesucht ist die Lösung des Anfangswertproblems für verschiedene Anfangswerte (Orte und Geschwindigkeiten) und Massen mi der Körper.
Lösung mit Matlab®
Die Lösung mit Matlab erfordert keine großen algebraischen Vorbereitungen - für die wir sonst Maxima einsetzten würden. Als äußere Kräfte treten nur die Feldkräfte der Gravitation zwischen den Körpern auf - die wir einfach hinschreiben und in Matlab implementieren können.
Declarations
Dafür verwenden wir das script T3BP.m, das die Funktionen
preprocess.m,ode45.m(solve) undpostprocess.m
aufruft. Die Klasse
planets.m
verwenden wir nur, um die Systemparameter "sys" bequem ansprechen zu können.
Zur Lösung des Anfangswertproblems rufen wir eine der ODE-Funktionen aus Matlab auf, die wir mit den Gleichgewichtsbedingungen unserer Funktion t3bpdydt.m füttern.
T3BP
|- preprocess
|- class sys=planets(data)
|- ode45
|- t3bpdydt
|- postprocess
Equilibrium Conditions
Die Gravitationskräfte zwischen den zwei Körpern i und j erfasst
mit der Gravitationskonstanten
Dabei gehen die Wirkungslinien der Kräfte durch die Massenmittelpunkte der Körper, die Körper ziehen sich gegenseitig an. Damit ist
- ,
wobei der Einheitsvektor der Anziehungskraft - in diesem Fall von i nach j - ist.
Die Bewegungsgleichungen schreiben wir mit in Vektorschreibweise für Körper i als
- .
Dabei ist z.B. i=1 und =2,3.
Die drei Bewegungsgleichungen in den drei räumlichen Koordinaten ui formulieren wir in dimensionslosen Koordinaten. Dafür brauchen wir drei unabhängige Referenzgrößen, hier wählen wir
Uns fehlt noch die Referent-Zeit T, die wir aus
erhalten. Damit ist .
Damit können wir schreiben:
Einsetzen und Kürzen liefert uns dann die dimensionslosen Bewegungsgleichungen
- .
Diese Gleichgewichtsbeziehungen implementieren wir in der Funktion t3bpdydt.m, die vom Löser ODE45 aufgerufen wird.
function dydt = t3bpdydt(t,y,sys)
% implementation of ode
% sys holds system parameters
% get coordinates
for body = 1:3
u(body,1:3) = transpose(y(3*(body-1)+1:3*body,1));
end
r = zeros(3,3,3);
e = zeros(3,3,3);
% compose vectors, unit vectors and distances
r(1,2,:) = u(2,:)-u(1,:); % this from m[1] to m[2]
:
:
:
% mass 3
dydt(9+7:9+9,1)=sys.theta(1)/R(3,1)*e(3,1,:)+sys.theta(2)/R(3,2)*e(3,2,:);
%% velocities
dydt(1:9,1) = y(10:18,1);
%%
waitbar(t / sys.tEnd);
end
Solving
Die Lösung des Anfangswertproblems übertragen wir der Matlab-Routine ODE45.
Dabei organisieren wir die Zustandsgrößen so, dass in y0 zunächst die 9 Anfangsverschiebungen und dann die 9 Anfangsgeschwindigkeiten stehen.
Wir lösen dann
mit
Die sind Komponentenweise die Geschwindigkeiten, also z.B.
- .
%% solve IVP
% set-up numerical paramters
tspan = 0:sys.tEnd/1000:sys.tEnd;
u0 = [transpose(sys.u0(1,:));transpose(sys.u0(2,:));transpose(sys.u0(3,:))]/sys.L;
v0 = [transpose(sys.v0(1,:));transpose(sys.v0(2,:));transpose(sys.v0(3,:))]*sys.T/sys.L;
% initial values from sys structured for ODE45
y0 = [u0;v0];
h = waitbar(0,'solving ODE - please wait...');
%
[t,y] = ode45(@(t,y)t3bpdydt(t,y,sys),tspan,y0);
close(h);
Matlab©-files
Die Datei-Struktur des Projekts zeigt das Bild links mit dem Skript T3BP.m. Classes und Functions sind in den jeweiligen Ordnern. Die Excel-Datei hält alle System-Parameter.
Den komplette Quellcode zu diesem Programm können Sie über dieses ZIP-File rechts herunterladen.

download compressed archive →
Post-Processing
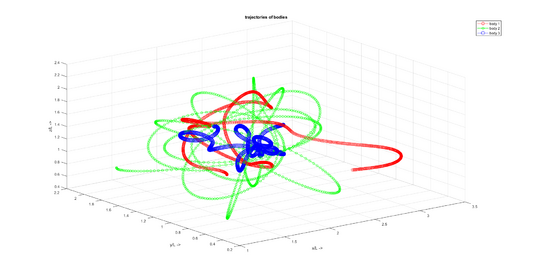
Uns interessieren natürlich die Trajektorien der Körper im Raum - dabei zeichnen wir die Körper-Durchmesser entsprechend Ihrer Masse. Die Darstellung ist nicht maßstäblich.
Zur Kontrolle können wir prüfen, ob die ODE-Routine im Rahmen der numerischen Genauigkeit die Erhaltungssätze der Mechanik erfüllt. Das machen wir hier am Beispiel des Impulssatzes: die Summe der Bewegungsgrößen jeweils in die drei Raumrichtungen muss gleich bleiben:

.
Und das tut sie offensichtlich auch - im Rahmen der numerischen Genauigkeit.
Und schließlich schauen wir uns die Bewegung der drei Körper in einer Animation über der Zeit an - hier über einen Zeitraum 4375 Jahren.
nothing here
Literature