Gelöste Aufgaben/Kita: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| (32 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 11: | Zeile 11: | ||
==Aufgabenstellung== | ==Aufgabenstellung== | ||
<onlyinclude> | <onlyinclude> | ||
[[Datei:Kita-01.png| | [[Datei:Kita-01.png|150px|left|mini|Lageplan]] | ||
Das skizzierte System ist ein Mast unter einer linear veränderlichen Windlast, der durch drei gleichmäßig über den Umfang verteilten Stäbe abgestützt wird. | Das skizzierte System ist ein Mast unter einer linear veränderlichen Windlast, der durch drei gleichmäßig über den Umfang verteilten Stäbe abgestützt wird. | ||
Gesucht ist die analytische Lösung für ein Euler-Bernoulli-Modell des elastischen Mastes und der drei Dehnstäbe. | Gesucht ist die analytische Lösung für ein Euler-Bernoulli-Modell des elastischen Mastes und der drei Dehnstäbe. | ||
</onlyinclude> | </onlyinclude> | ||
[[Datei:Kita-02.png| | [[Datei:Kita-02.png|190px|right|mini|Sicht auf den Mast]] | ||
Der Mast steht senkrecht dabei auf einer ebenen Unterlage mit dem festen Gelenklager „''O''“ und ist durch drei Stäbe abgestützt. Alle Stäbe sind in Punkt „''H''“ mit dem Mast verbunden und in den Punkten „''A''“, „''B''“ und „''C''“ gelenkig gelagert. | Der Mast steht senkrecht dabei auf einer ebenen Unterlage mit dem festen Gelenklager „''O''“ und ist durch drei Stäbe abgestützt. Alle Stäbe sind in Punkt „''H''“ mit dem Mast verbunden und in den Punkten „''A''“, „''B''“ und „''C''“ gelenkig gelagert. | ||
Die Lager A, B und C sind gleichmäßig in einem Radius von R um O herum auf der Unterlage verteilt. Die Windlast hat den Maximalwert ''q<sub>T</sub>'' und wirkt in der Ebene, die durch die Punkte A, O und H aufgespannt werden. Für die Geometrie des Masts gilt <i>h<sub>1</sub> = 2 h<sub>2</sub>, h<sub>2</sub> = √2 R</i>, außerdem sei die Dehnsteifigkeiten der Stäbe <i>E A<sub>2</sub>=2 E A<sub>1</sub>,E A<sub>3</sub>=E A<sub>1</sub></i>. | Die Lager A, B und C sind gleichmäßig in einem Radius von ''R'' um ''O'' herum auf der Unterlage verteilt. Die Windlast hat den Maximalwert ''q<sub>T</sub>'' und wirkt in der Ebene, die durch die Punkte ''A, O'' und ''H'' aufgespannt werden. Für die Geometrie des Masts gilt <i>h<sub>1</sub> = 2 h<sub>2</sub>, h<sub>2</sub> = √2 R</i>, außerdem sei die Dehnsteifigkeiten der Stäbe <i>E A<sub>2</sub>=2 E A<sub>1</sub>,E A<sub>3</sub>=E A<sub>1</sub></i>. | ||
Der Mast hat ein zylindrisches Profil mit Innen- und Außendurchmesser <i>d<sub>i</sub>, d<sub>a</sub></i>. | Der Mast hat ein zylindrisches Profil mit Innen- und Außendurchmesser <i>d<sub>i</sub>, d<sub>a</sub></i>. | ||
[[Datei:Kita-03.png|65px|mini|Mastprofil]] | |||
Ein Knicken der drei Stäbe sei ausgeschlossen. | Ein Knicken der drei Stäbe sei ausgeschlossen. | ||
| Zeile 31: | Zeile 31: | ||
<!--------------------------------------------------------------------------------> | <!--------------------------------------------------------------------------------> | ||
{{MyCodeBlock|title=Header | {{MyCodeBlock|title=Header | ||
|text=Kern der Lösung ist die Berechnung der Integrationskonstanten des Euler-Bernoulli-Balkens. In diesem Beispiel führen wir zusätzliche | |text=Kern der Lösung ist die Berechnung der Integrationskonstanten des Euler-Bernoulli-Balkens. In diesem Beispiel führen wir zusätzliche Abkürzungen als Variablen ein, um die Rand- und Übergangsbedingungen einfacher formulieren zu können. | ||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
| Zeile 53: | Zeile 53: | ||
EA_2& = &2 EA_1,\\ | EA_2& = &2 EA_1,\\ | ||
EA_3& = &EA_1,\\ | EA_3& = &EA_1,\\ | ||
h_1 & = &2 h_2, \\ | h_1 & = &2\;h_2, \\ | ||
h_2 & = &\sqrt{2 | h_2 & = &\sqrt{2}\;R \text{ und }\\ | ||
EA_1& = &\alpha EI/R^2 | EA_1& = &\alpha\;EI/R^2 | ||
\end{array}</math> | \end{array}</math> | ||
[[Datei:Kita-14.png|150px|right|mini|''x-y-z''-Koordinaten]] | |||
und definieren für die Berechnung der Stabkräfte die Referenzorte von <i>A, B, C</i> und <i>H</i> wie skizziert im <i>x, y, z</i> Koordinatensystem zu | und definieren für die Berechnung der Stabkräfte die Referenzorte von <i>A, B, C</i> und <i>H</i> wie rechts skizziert im <i>x, y, z</i> Koordinatensystem zu | ||
::<math> | ::<math> | ||
\underline{r}_H = \begin{pmatrix}h_1\\0\\ 0\end{pmatrix}, | \underline{r}_H = \begin{pmatrix}h_1\\0\\ 0\end{pmatrix}, | ||
| Zeile 68: | Zeile 68: | ||
::<math> | ::<math> | ||
\underline{r}_1 = \underline{r}_A-\underline{r}_H, | \underline{r}_1 = \underline{r}_A-\underline{r}_H, | ||
\underline{r}_2 = \underline{r}_B-\underline{r}_H und | \underline{r}_2 = \underline{r}_B-\underline{r}_H \text{ und } | ||
\underline{r}_3 = \underline{r}_C-\underline{r}_H, | \underline{r}_3 = \underline{r}_C-\underline{r}_H, | ||
</math> | </math> | ||
| Zeile 113: | Zeile 113: | ||
Wir nutzen die Standard-Nomenklatur für den Euler-Bernoulli-Balken und schrieben jeweils die Gleichgewichtsbedingungen | Wir nutzen die Standard-Nomenklatur für den Euler-Bernoulli-Balken und schrieben jeweils die Gleichgewichtsbedingungen | ||
<table style="background-color:white; margin-right:14px;"> | <table style="background-color:white; margin-right:14px;"> | ||
<tr><th></th><th> ... in z-Richtung als</th><th> ... in y-Richtung als</th></tr> | <tr><th></th><th> ... in ''z''-Richtung als</th><th> ... in ''y''-Richtung als</th></tr> | ||
<tr><td></td> | <tr><td></td> | ||
<td><math>{\displaystyle E\,I\,w_{i}^{IV}(x)=q_{z},\;\;i=\{1,2\}}</math>.</td> | <td><math>{\displaystyle E\,I\,w_{i}^{IV}(x)=q_{z},\;\;i=\{1,2\}}</math>.</td> | ||
| Zeile 122: | Zeile 122: | ||
<tr><td>... die Querschnitts-Auslenkung: </td><td><math>w_{i}(x)</math></td> | <tr><td>... die Querschnitts-Auslenkung: </td><td><math>w_{i}(x)</math></td> | ||
<td><math>v_{i}(x)</math></td></tr> | <td><math>v_{i}(x)</math></td></tr> | ||
<tr><td>... die Querschnitts-Verdrehung: </td><td><math>\ | <tr><td>... die Querschnitts-Verdrehung: </td><td><math>\varphi _{i}(x)= \frac{\displaystyle d \,w_{i}(x)}{\displaystyle d\,x }</math></td> | ||
<td><math>\psi _{i}(x)= \frac{\displaystyle d \,v_{i}(x)}{\displaystyle d\,x }</math></td></tr> | <td><math>\psi _{i}(x)= \frac{\displaystyle d \,v_{i}(x)}{\displaystyle d\,x }</math></td></tr> | ||
<tr><td>... das Biege-Moment: </td><td><math> M_{y,i}(x)=-EI \frac{\displaystyle d^{2}\,w_{i}(x)}{\displaystyle d\,x^{2}}</math></td> | <tr><td>... das Biege-Moment: </td><td><math> M_{y,i}(x)=-EI \frac{\displaystyle d^{2}\,w_{i}(x)}{\displaystyle d\,x^{2}}</math></td> | ||
| Zeile 130: | Zeile 130: | ||
</table> | </table> | ||
Für die Streckenlasten auf den Mast gilt je Bereich "i": | Für die Streckenlasten auf den Mast gilt je Bereich "i" die lineare Funktion: | ||
* ... in z-Richtung: <math>q_{z,i}(x) = q_{z,i-1}\cdot(1-\frac{\displaystyle x_i}{\displaystyle h_i})+q_{z,i}\cdot \frac{\displaystyle x_i}{\displaystyle h_i}</math> und | * ... in ''z''-Richtung: <math>q_{z,i}(x) = q_{z,i-1}\cdot(1-\frac{\displaystyle x_i}{\displaystyle h_i})+q_{z,i}\cdot \frac{\displaystyle x_i}{\displaystyle h_i}</math> und | ||
* ... in y-Richtung: <math>q_{y,i}(x) = 0 </math> | * ... in ''y''-Richtung: <math>q_{y,i}(x) = 0 </math> | ||
wobei | wobei an den Knotenpunkten dies gilt: | ||
::<math> | ::<math> | ||
\begin{array}{ccl} | \begin{array}{ccl} | ||
q_{z, | q_{z,2} &=& {\color{red}-}q_T\\ | ||
q_{z,1} &=& {\color{red}-}q_T\cdot\frac{\displaystyle h_1}{\displaystyle h_1+h_2}\\ | q_{z,1} &=& {\color{red}-}q_T\cdot\frac{\displaystyle h_1}{\displaystyle h_1+h_2}\\ | ||
q_{z, | q_{z,0} &=& 0. | ||
\end{array} | \end{array} | ||
</math> | </math> | ||
Mit diesen Ansätzen erhalten wir aus der Integration der Differentialbeziehung für den Euler-Bernoulli-Balken diese generischen (weil mit Integrationskonstanten) Lösungen: | Mit diesen Ansätzen erhalten wir aus der Integration der Differentialbeziehung für den Euler-Bernoulli-Balken diese generischen (weil mit Integrationskonstanten behaftete) Lösungen: | ||
<table style="background-color:white; margin-right:14px;"> | <table style="background-color:white; margin-right:14px;"> | ||
<tr><th>Richung ...</th><th>z</th><th>y</th></tr> | <tr><th>Richung ...</th><th>''z''</th><th>''y''</th></tr> | ||
<tr><th>Bereich I:</th><td><math>w_{ I}(x)=-\frac{q_T x^5}{120 \left( {h_2}+{h_1}\right) EI}+{c_1} \frac{{{x}^{3}}}{6}+{c_2} \frac{{{x}^{2}}}{2}+{c_3}\; x+{c_4}</math></td> | <tr><th>Bereich I:</th><td><math>w_{ I}(x)=-\frac{q_T x^5}{120 \left( {h_2}+{h_1}\right) EI}+{c_1} \frac{{{x}^{3}}}{6}+{c_2} \frac{{{x}^{2}}}{2}+{c_3}\; x+{c_4}</math></td> | ||
<td><math>v_{ I}(x)={c_5} \frac{{{x}^{3}}}{6}+{c_6} \frac{{{x}^{2}}}{2}+{c_7}\;x+{c_8}</math></td></tr> | <td><math>v_{ I}(x)={c_5} \frac{{{x}^{3}}}{6}+{c_6} \frac{{{x}^{2}}}{2}+{c_7}\;x+{c_8}</math></td></tr> | ||
| Zeile 149: | Zeile 149: | ||
<td><math>v_{II}(x)={c_{13}} \frac{{{x}^{3}}}{6}+{c_{14}} \frac{{{x}^{2}}}{2}+{c_{15}}\;x+{c_{16}}</math></td></tr> | <td><math>v_{II}(x)={c_{13}} \frac{{{x}^{3}}}{6}+{c_{14}} \frac{{{x}^{2}}}{2}+{c_{15}}\;x+{c_{16}}</math></td></tr> | ||
</table> | </table> | ||
Wir haben also Bereich I und II für Richtungen z und y mit jeweils 4 integrationskonstanten - insgesamt 16. | Wir haben also Bereich I und II für Richtungen z und y mit jeweils 4 integrationskonstanten - das macht insgesamt 16 zu bestimmende Variablen. | ||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
| Zeile 183: | Zeile 183: | ||
Die Zugkräfte <i>S<sub>i</sub></i> in den drei Dehnstäben erhalten wir aus der Stab-Längung <math>\Delta L_i</math>, also | Die Zugkräfte <i>S<sub>i</sub></i> in den drei Dehnstäben erhalten wir aus der Stab-Längung <math>\Delta L_i</math>, also | ||
::<math>S_i = EA_i \frac{\displaystyle \Delta L_i}{\displaystyle L}</math> | ::<math>S_i = EA_i \frac{\displaystyle \Delta L_i}{\displaystyle L}</math> | ||
[[Datei:Kita-11.png|150px|right|mini|Freikörperbild in der x-z-Ebene]] | |||
::<math>\underline{S}_i = S_i \cdot \underline{e}_i</math> | [[Datei:Kita-12.png|180px|right|mini|Freikörperbild in der y-z-Ebene]] | ||
Die Bilder rechts zeigen die Stabkräfte am freigeschnittenen Punkt <i>H</i> des Masts. | |||
Bei der Berechnung der Stabkräfte ist <math>\Delta L_i</math> die Längung von Stab <i>i</i>. Die Kraft hat als Richtung <math>\underline{e}_i</math>, also ist | |||
::<math>\underline{S}_i = S_i \cdot \underline{e}_i</math>. | |||
Es fehlt nur noch die Stablängung <math>\Delta L_i</math> je Stab – und die bekommen wir aus dem Vergleich der Geometrie des Stabes im verformten und unverformten Zustand. | Es fehlt nur noch die Stablängung <math>\Delta L_i</math> je Stab – und die bekommen wir aus dem Vergleich der Geometrie des Stabes im verformten und unverformten Zustand. | ||
| Zeile 191: | Zeile 194: | ||
und die Koeffizienten der Stab-Vektoren sind nun | und die Koeffizienten der Stab-Vektoren sind nun | ||
::<math>\tilde{\underline{r}}_1 = \underline{r}_A - \tilde{\underline{r}}_H, \ldots</math>. | ::<math>\tilde{\underline{r}}_1 = \underline{r}_A - \tilde{\underline{r}}_H, \ldots</math>. | ||
Die Differenzlänge erhalten wir – nach dem gleichen Schema wie oben aus | Die Differenzlänge erhalten wir – nach dem gleichen Schema wie oben – aus | ||
::<math>\Delta L_i = ||\tilde{\underline{r}}_i||-L</math>. | ::<math>\Delta L_i = ||\tilde{\underline{r}}_i||-L</math>. | ||
In | In | ||
| Zeile 197: | Zeile 200: | ||
steht nun allerdings ein komplizierter, nichtlinearer Ausdruck. | steht nun allerdings ein komplizierter, nichtlinearer Ausdruck. | ||
Den linearisieren wir, schreiben also | Den linearisieren wir, schreiben also | ||
::<math>\Delta L_i | ::<math>\Delta L_i := \left.\frac{\partial \Delta L_i}{\partial V_H}\right\vert_{V_H=0, W_H =0} \cdot V_H + \left.\frac{\partial \Delta L_i}{\partial W_H}\right\vert_{V_H=0, W_H =0} \cdot W_H</math> | ||
und erhalten damit | und erhalten damit | ||
::<math>\begin{array}{llll}S_1 &=&R \cdot \frac{\displaystyle E\,A_1}{\displaystyle L}&\;\;\;W_H\\ | ::<math>\begin{array}{llll}S_1 &=&R \cdot \frac{\displaystyle E\,A_1}{\displaystyle L^2}&\cdot\;\;\;\;\;\;\;W_H\\ | ||
S_2 &=&R \cdot \frac{\displaystyle E\,A_2}{\displaystyle L}&\left(-\frac{\displaystyle 1}{\displaystyle 2} W_H + \frac{\displaystyle \sqrt{3}}{\displaystyle 2} V_H\right)\\ | S_2 &=&R \cdot \frac{\displaystyle E\,A_2}{\displaystyle L^2}&\cdot\left(-\frac{\displaystyle 1}{\displaystyle 2} W_H + \frac{\displaystyle \sqrt{3}}{\displaystyle 2} V_H\right)\\ | ||
S_3 &=&R \cdot \frac{\displaystyle E\,A_3}{\displaystyle L}&\left(-\frac{\displaystyle 1}{\displaystyle 2} W_H - \frac{\displaystyle \sqrt{3}}{\displaystyle 2} V_H\right) | S_3 &=&R \cdot \frac{\displaystyle E\,A_3}{\displaystyle L^2}&\cdot\left(-\frac{\displaystyle 1}{\displaystyle 2} W_H - \frac{\displaystyle \sqrt{3}}{\displaystyle 2} V_H\right) | ||
\end{array}</math> | \end{array}</math> | ||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
/*******************************************************/ | |||
/* forces S[i] in supporing rods */ | |||
/* S[i] as a function of W[H] and V[H] *****************/ | |||
/* *****************************************************/ | |||
ΔL: subst(geo,[r[A] - (r[H]+matrix([0,V[H],W[H]])), | |||
r[B] - (r[H]+matrix([0,V[H],W[H]])), | |||
r[C] - (r[H]+matrix([0,V[H],W[H]]))]); | |||
ΔL: makelist(sqrt(ΔL[i].ΔL[i])-subst(geo,L),i,1,3); | |||
displ: [W[H],V[H]]; | |||
null : makelist(displ[i]=0,i,1,2); | |||
/* linearize .... */ | |||
ΔL: sum(subst(null, diff(ΔL,displ[j]))*displ[j],j,1,2); | |||
S : makelist(EA[i]*ΔL[i]/subst(geo,L),i,1,3); | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
<!--------------------------------------------------------------------------------> | <!--------------------------------------------------------------------------------> | ||
{{MyCodeBlock|title=Boundary- and Transition-Conditions | {{MyCodeBlock|title=Boundary- and Transition-Conditions | ||
|text= | |text= | ||
Aus der Lösung der Differentialgleichungen für zwei Raumrichtungen und zwei Bereiche haben wir 16 Integrationskonstanten, die wir bestimmen müssen. Hinzu kommen <i>V<sub>H</sub></i> und <i>W<sub>H</sub></i> für den Knoten <i>H</i>. Um hier konsistent zu sein, führen wir für die Knoten <i>H</i> und <i>T</i> – "Top", die Mastspitze – die Koordinaten der Auslenkung und Kippung der Querschnitte ein, also zusammen die 8 Knotenvariablen | |||
<table style="background-color:white; margin-right:14px; border: 1px solid black; border-spacing: 30px;"> | |||
<tr><th>Richtung</th><th>z</th><th>y</th></tr> | |||
<tr><td>Knoten T<br/>Auslenkung<br/>Kippwinkel</td><td><br/><math>W_T</math>,<br/><math>\Phi_T</math></td><td><br/><math>V_T</math>,<br/><math>\Psi_T</math></td></tr> | |||
<tr><td>Knoten H<br/>Auslenkung<br/>Kippwinkel</td><td><br/><math>W_H</math>,<br/><math>\Phi_H</math></td><td><br/><math>V_H</math>,<br/><math>\Psi_H</math></td></tr> | |||
<tr><td>Knoten 0<br/>Auslenkung<br/>Kippwinkel</td><td><br/><math> 0 </math>,<br/><math> c_3 </math></td><td><br/><math> 0 </math>,<br/><math> c_7 </math></td></tr> | |||
</table> | |||
In ''O'' hätten wir auch noch die Variablen <math>\Phi_O</math> und <math>\Psi_O</math> einführen könnten. Die sind allerdings identisch mit <math>c_3</math> und <math>c_7</math>. | |||
Alle Unbekannten fassen wir nun in | |||
::<math>\underline{c} = \left(\begin{array}{l}c_{01}\\c_{02}\\\ldots\\c_{15}\\c_{16}\\W_H\\V_H\\\Phi_H\\\Psi_H\\W_T\\V_T\\\Phi_T\\\Psi_T\end{array}\right)</math> | |||
zusammen. | |||
Für diese 24 Unbekannten brauchen wir nun 24 Gleichungen – Geometriebedingungen und Kräfte-/Momentengleichgewichte. | |||
==== ... aus Rand "<i>O</i>"==== | |||
Das gelenkige Lager in ''O'' erlaubt keine Verschiebung und es nimmt keine Momente auf. | |||
Daraus ergeben sich die '''Geometrischen Bedingungen:''' | |||
<ol start="1"> | |||
<li><math>w_{ I}(0) = 0</math></li> | |||
<li><math>v_{ I}(0) = 0</math></li> | |||
</ol> | |||
und die '''Kraft- und Momenten-Randbedingungen:''' | |||
<ol start="3"> | |||
<li><math>M_{z, I}(0) = 0</math></li> | |||
<li><math>M_{y, I}(0) = 0</math></li> | |||
</ol> | |||
==== ... aus Übergang <i>H</i>==== | ==== ... aus Übergang "<i>H</i>"==== | ||
'''Geometrische Bedingungen:''' | |||
<ol start="5"> | |||
<li><math>w_{ I}(h_1) = W_H</math></li> | |||
<li><math>v_{ I}(h_1) = V_H</math></li> | |||
<li><math>w_{II}( 0 ) = W_H</math></li> | |||
<li><math>v_{II}( 0 ) = V_H</math></li> | |||
<li><math>\varphi_{ I}(h_1) = \Phi_H</math></li> | |||
<li><math>\psi_{ I}(h_1) = \Psi_H</math></li> | |||
<li><math>\varphi_{II}( 0 ) = \Phi_H</math></li> | |||
<li><math>\psi_{II}( 0 ) = \Psi_H</math></li> | |||
</ol> | |||
'''Kraft- und Momenten-Randbedingungen:''' | |||
Hier wird es spannend: durch die drei Stäbe werden Kräfte eingeleitet, | |||
[[Datei:Kita-13.png|180px|right|mini|Schnittbild für Knoten ''H''<br/>hier ohne Schnittmomente]] | |||
Einfach sind die Momenten-Gleichgewichtsbedingungen am Knoten ''H'' - hier wird kein externes Moment eingeleitet, die beiden Schnittmomente müssen gleich sein: | |||
<ol start="13"> | |||
<li><math>M_{y, I}(h_1) = M_{y,II}( 0 )</math></li> | |||
<li><math>M_{z, I}(h_1) = M_{z,II}( 0 )</math></li> | |||
</ol> | |||
Für die Kraft-Übergangsbedingungen in <i>y</i>- und <i>z</i>-Richtung müssen wir nun allerdings die Seilkräfte mit einbeziehen. | |||
<ol start="15"> | |||
<li><math>Q_{y, I}(h_1) = Q_{y,II}( 0 ) + \sum_{k=1}^3 S_i \cdot e_{i,y}</math></li> | |||
<li><math>Q_{z, I}(h_1) = Q_{z,II}( 0 ) + \sum_{k=1}^3 S_i \cdot e_{i,z}</math></li> | |||
</ol> | |||
Dabei nehmen wir vom Einheitsvektor nur die Komponente der jeweiligen Raumrichtung, also z.B. <math>e_{i,y}</math> aus <math>\underline{e}_{i}=\left(\begin{array}{c}e_{i,x}\\e_{i,y}\\e_{i,z}\end{array}\right)</math>. | |||
==== ... aus Rand "<i>T</i>"==== | |||
'''Geometrische Bedingungen:''' | |||
Für die geometrischen Randbedingen haben wir nur die Gleichungen, die unsere Abkürzungen einführen, also | |||
<ol start="17"> | |||
<li><math>w_{II}(h_2) = W_T </math></li> | |||
<li><math>v_{II}(h_2) = V_T </math></li> | |||
<li><math>\varphi_{II}(h_2) = \Phi_T </math></li> | |||
<li><math>\psi_{II}(h_2) = \Psi_T </math></li> | |||
</ol> | |||
==== | '''Kraft- und Momenten-Randbedingungen:''' | ||
Hier ist Rand frei: Kräfte und Momente in ''T'' müssen Null sein: | |||
<ol start="21"> | |||
<li><math>M_{y,II}(h_2) = 0 </math></li> | |||
<li><math>M_{z,II}(h_2) = 0 </math></li> | |||
<li><math>Q_{y,II}(h_2) = 0 </math></li> | |||
<li><math>Q_{z,II}(h_2) = 0 </math></li> | |||
</ol> | |||
Damit sind wir komplett - wir haben 24 Gleichungen für 24 Unbekannte. | |||
Das Gleichungssystem können wir nun als | |||
::<math>\underline{\underline{A}}\cdot\underline{c}=\underline{b}</math> | |||
schreiben - oder mit den oben angegebenen Systemparametern ausgeschreiben als | |||
::<math> | |||
\begin{pmatrix}0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ | |||
0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ | |||
0 & -EI & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ | |||
0 & 0 & 0 & 0 & 0 & EI & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ | |||
\frac{{{h}_{1}^{3}}}{6} & \frac{{{h}_{1}^{2}}}{2} & {h_1} & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -1 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ | |||
0 & 0 & 0 & 0 & \frac{{{h}_{1}^{3}}}{6} & \frac{{{h}_{1}^{2}}}{2} & {h_1} & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -1 & 0 & 0 & 0 & 0 & 0 & 0\\ | |||
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & -1 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ | |||
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & -1 & 0 & 0 & 0 & 0 & 0 & 0\\ | |||
\frac{{{h}_{1}^{2}}}{2} & {h_1} & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -1 & 0 & 0 & 0 & 0 & 0\\ | |||
0 & 0 & 0 & 0 & \frac{{{h}_{1}^{2}}}{2} & {h_1} & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -1 & 0 & 0 & 0 & 0\\ | |||
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -1 & 0 & 0 & 0 & 0 & 0\\ | |||
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & -1 & 0 & 0 & 0 & 0\\ | |||
-{h_1} & -1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ | |||
0 & 0 & 0 & 0 & {h_1} & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ | |||
-1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \frac{\left( {EA_3}+{EA_2}+4 {EA_1}\right) {{R}^{2}}}{\sqrt{{{R}^{2}}+{{h}_{1}^{2}}} \left( 4 EI {{R}^{2}}+4 {{h}_{1}^{2}}\, EI\right) } & \frac{\left( \sqrt{3} {EA_3}-\sqrt{3} {EA_2}\right) {{R}^{2}}}{\sqrt{{{R}^{2}}+{{h}_{1}^{2}}} \left( 4 EI {{R}^{2}}+4 {{h}_{1}^{2}}\, EI\right) } & 0 & 0 & 0 & 0 & 0 & 0\\ | |||
0 & 0 & 0 & 0 & -1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & \frac{\left( \sqrt{3} {EA_3}-\sqrt{3} {EA_2}\right) {{R}^{2}}}{\sqrt{{{R}^{2}}+{{h}_{1}^{2}}} \left( 4 EI {{R}^{2}}+4 {{h}_{1}^{2}}\, EI\right) } & \frac{\left( 3 {EA_3}+3 {EA_2}\right) {{R}^{2}}}{\sqrt{{{R}^{2}}+{{h}_{1}^{2}}} \left( 4 EI {{R}^{2}}+4 {{h}_{1}^{2}}\, EI\right) } & 0 & 0 & 0 & 0 & 0 & 0\\ | |||
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \frac{{{h}_{2}^{3}}}{6} & \frac{{{h}_{2}^{2}}}{2} & {h_2} & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -1 & 0 & 0 & 0\\ | |||
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \frac{{{h}_{2}^{3}}}{6} & \frac{{{h}_{2}^{2}}}{2} & {h_2} & 1 & 0 & 0 & 0 & 0 & 0 & -1 & 0 & 0\\ | |||
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \frac{{{h}_{2}^{2}}}{2} & {h_2} & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -1 & 0\\ | |||
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \frac{{{h}_{2}^{2}}}{2} & {h_2} & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -1\\ | |||
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -{h_2} & -1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ | |||
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {h_2} & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ | |||
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ | |||
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\end{pmatrix} | |||
\cdot \underline{c} | |||
= | |||
\begin{pmatrix}0\\ | |||
0\\ | |||
0\\ | |||
0\\ | |||
\frac{{{h}_{1}^{5}} {q_T}}{\left( 120 {h_2}+120 {h_1}\right) \, EI}\\ | |||
0\\ | |||
0\\ | |||
0\\ | |||
\frac{{{h}_{1}^{4}} {q_T}}{\left( 24 {h_2}+24 {h_1}\right) \, EI}\\ | |||
0\\ | |||
0\\ | |||
0\\ | |||
-\frac{{{h}_{1}^{3}} {q_T}}{\left( 6 {h_2}+6 {h_1}\right) \, EI}\\ | |||
0\\ | |||
-\frac{{{h}_{1}^{2}} {q_T}}{\left( 2 {h_2}+2 {h_1}\right) \, EI}\\ | |||
0\\ | |||
\frac{\left( {{h}_{2}^{5}}+5 {h_1} {{h}_{2}^{4}}\right) {q_T}}{\left( 120 {h_2}+120 {h_1}\right) \, EI}\\ | |||
0\\ | |||
\frac{\left( {{h}_{2}^{4}}+4 {h_1} {{h}_{2}^{3}}\right) {q_T}}{\left( 24 {h_2}+24 {h_1}\right) \, EI}\\ | |||
0\\ | |||
-\frac{\left( {{h}_{2}^{3}}+3 {h_1} {{h}_{2}^{2}}\right) {q_T}}{\left( 6 {h_2}+6 {h_1}\right) \, EI}\\ | |||
0\\ | |||
-\frac{\left( {{h}_{2}^{2}}+2 {h_1} {h_2}\right) {q_T}}{\left( 2 {h_2}+2 {h_1}\right) \, EI}\\ | |||
0\end{pmatrix} | |||
</math> | |||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
/******************************************************/ | |||
/* Boundary Value Problem Formulation */ | |||
/* ****************************************************/ | |||
/* point "O" - geometry */ | |||
BC: [subst(x= 0 , subst(sol[1][1],w(x)) )= 0 , | |||
subst(x= 0 , subst(sol[2][1],v(x)) )= 0 , | |||
/* point "O" - bending moments */ | |||
subst(x= 0 , subst(sol[1][1],M[y](x)) )= 0 , | |||
subst(x= 0 , subst(sol[2][1],M[z](x)) )= 0 , | |||
/* point "H" - geometry */ | |||
subst(x= h[1], subst(sol[1][1],w(x)) )=W[H], | |||
subst(x= h[1], subst(sol[2][1],v(x)) )=V[H], | |||
subst(x= 0 , subst(sol[1][2],w(x)) )=W[H], | |||
subst(x= 0 , subst(sol[2][2],v(x)) )=V[H], | |||
subst(x= h[1], subst(sol[1][1],φ(x)) )=Φ[H], | |||
subst(x= h[1], subst(sol[2][1],ψ(x)) )=Ψ[H], | |||
subst(x= 0 , subst(sol[1][2],φ(x)) )=Φ[H], | |||
subst(x= 0 , subst(sol[2][2],ψ(x)) )=Ψ[H], | |||
/* point "H" - bending moments */ | |||
subst(x= h[1], subst(sol[1][1],M[y](x)) )=subst(x= 0 , subst(sol[1][2],M[y](x)) ), | |||
subst(x= h[1], subst(sol[2][1],M[z](x)) )=subst(x= 0 , subst(sol[2][2],M[z](x)) ), | |||
/* point "H" - forces */ | |||
subst(x= h[1], subst(sol[1][1],Q[z](x)) )=subst(x= 0 , subst(sol[1][2],Q[z](x)) ) + sum(S[i]*subst(geo,e[i]),i,1,3)[1][3], | |||
subst(x= h[1], subst(sol[2][1],Q[y](x)) )=subst(x= 0 , subst(sol[2][2],Q[y](x)) ) + sum(S[i]*subst(geo,e[i]),i,1,3)[1][2], | |||
/* point "T" (Top) - geometry */ | |||
subst(x= h[2], subst(sol[1][2],w(x)) )=W[T], | |||
subst(x= h[2], subst(sol[2][2],v(x)) )=V[T], | |||
subst(x= h[2], subst(sol[1][2],φ(x)) )=Φ[T], | |||
subst(x= h[2], subst(sol[2][2],ψ(x)) )=Ψ[T], | |||
/* point "T" (Top) - bending moment */ | |||
subst(x= h[2], subst(sol[1][2],M[y](x)) ) = 0, | |||
subst(x= h[2], subst(sol[2][2],M[z](x)) ) = 0, | |||
/* point "T" (Top) - forces */ | |||
subst(x= h[2], subst(sol[1][2],Q[z](x)) ) = 0, | |||
subst(x= h[2], subst(sol[2][2],Q[y](x)) ) = 0]; | |||
C: append(makelist(c[i],i,16), [W[H],V[H],Φ[H],Ψ[H],W[T],V[T],Φ[T],Ψ[T]]); | |||
scale: [1,1,1,1,1,1,1,1,1,1, | |||
1,1,EI,EI,EI,EI,1,1,1,1, | |||
EI,EI,EI,EI]; | |||
for i:1 thru 24 do BC[i]:BC[i]/scale[i]; | |||
ACM: ratsimp(augcoefmatrix(BC,C)); | |||
a: submatrix(ACM,25); | |||
b:-col(ACM,25); | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
| Zeile 238: | Zeile 414: | ||
<!--------------------------------------------------------------------------------> | <!--------------------------------------------------------------------------------> | ||
{{MyCodeBlock|title=Solving | {{MyCodeBlock|title=Solving | ||
|text= | |text= Dieses lineare Gleichungssystem kann man gerade noch analytisch lösen - wir finden die gesuchten Integrationskonstanten und Knotenvariablen | ||
::<math> | |||
\begin{array}{l} | |||
{c_1}=0\\ | |||
{c_2}=0\\ | |||
{c_3}=\frac{{{2}^{\frac{9}{2}}} {{R}^{3}} {q_T} \alpha -2187 {{R}^{3}} {q_T}}{180 EI \alpha }\\ | |||
{c_4}=0\\ | |||
{c_5}=0\\ | |||
{c_6}=0\\ | |||
{c_7}=-\frac{{{3}^{\frac{7}{2}}} {{R}^{3}} {q_T}}{20 EI \alpha }\\ | |||
{c_8}=0\\ | |||
{c_9}=\frac{5 R {q_T}}{3 \sqrt{2} EI}\\ | |||
{c_{10}}=- | |||
\frac{8 {{R}^{2}} {q_T}}{9 EI}\\ | |||
{c_{11}}=-\frac{{{2}^{\frac{13}{2}}} {{R}^{3}} {q_T} \alpha +2187 {{R}^{3}} {q_T}}{180 EI \alpha }\\ | |||
{c_{12}}=-\frac{243 {{R}^{4}} {q_T}}{5 \sqrt{2} EI \alpha }\\ | |||
{c_{13}}=0\\ | |||
{c_{14}}=0\\ | |||
{c_{15}}=-\frac{{{3}^{\frac{7}{2}}} {{R}^{3}} {q_T}}{20 EI \alpha }\\ | |||
{c_{16}}=-\frac{{{3}^{\frac{7}{2}}} {{R}^{4}} {q_T}}{5 \sqrt{2} EI \alpha }\\ | |||
{W_H}=-\frac{243 {{R}^{4}} {q_T}}{5 \sqrt{2} EI \alpha }\\ | |||
{V_H}=-\frac{{{3}^{\frac{7}{2}}} {{R}^{4}} {q_T}}{5 \sqrt{2} EI \alpha }\\ | |||
{{\Phi }_H}=-\frac{{{2}^{\frac{13}{2}}} {{R}^{3}} {q_T} \alpha +2187 {{R}^{3}} {q_T}}{180 EI \alpha }\\ | |||
{{\Psi }_H}=-\frac{{{3}^{\frac{7}{2}}} {{R}^{3}} {q_T}}{20 EI \alpha }\\ | |||
{W_T}=- | |||
\frac{70 {{R}^{4}} {q_T} \alpha +2187 \sqrt{2} {{R}^{4}} {q_T}}{60 EI \alpha }\\ | |||
{V_T}=-\frac{{{3}^{\frac{9}{2}}} {{R}^{4}} {q_T}}{5 {{2}^{\frac{3}{2}}} EI \alpha }\\ | |||
{{\Phi }_T}=-\frac{119 \sqrt{2} {{R}^{3}} {q_T} \alpha +2187 {{R}^{3}} {q_T}}{180 EI \alpha }\\ | |||
{{\Psi }_T}=-\frac{{{3}^{\frac{7}{2}}} {{R}^{3}} {q_T}}{20 EI \alpha } | |||
\end{array} | |||
</math> | |||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
/*******************************************************/ | |||
/* solve for integration constants */ | |||
/* *****************************************************/ | |||
consts: ratsimp(solve(ratsimp(subst(params,BC)),C)[1]); | |||
sol: subst(consts,sol); | |||
toReplace: [x=ξ*h[1],x=ξ*h[2]]; | |||
for dir: 1 thru 2 do | |||
for sec: 1 thru 2 do | |||
(print(dir,sec), | |||
for elem: 1 thru 4 do | |||
sol[dir][sec][elem]: lhs(sol[dir][sec][elem])=subst(toReplace[sec],rhs(sol[dir][sec][elem]))); | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
| Zeile 252: | Zeile 465: | ||
<!--------------------------------------------------------------------------------> | <!--------------------------------------------------------------------------------> | ||
{{MyCodeBlock|title=Post-Processing | {{MyCodeBlock|title=Post-Processing | ||
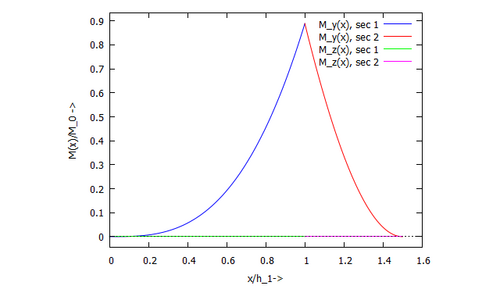
|text= | |text=Die Verläufe der Auslenkung und Schnittkräfte - hier exemplarisch das Biegemoment - können wir nun plotten: | ||
<table> | |||
<tr><td>[[Datei:Kita-21.png|500px|mini|Auslenkung der Querschnitte]]</td><td>[[Datei:Kita-22.png|500px|mini|Biegemomente]]</td></tr> | |||
</table> | |||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
/*******************************************************/ | |||
/* post-processing */ | |||
/*******************************************************/ | |||
/* what is a reasonable size is α ? */ | |||
/* geopar: [A[1]= π/ 4*d[r]^2, d[r]=1*cm, | |||
I = π/64*(d[o]^4-d[i]^4), d[o]=10*cm, d[i]=9*cm, | |||
R = h[2]/sqrt(2), h[2]=500*cm, | |||
α = A[1]*R^2/I ] */ | |||
sol: ratsimp(subst([α=500],subst(params,sol))); | |||
toPlot: ratsimp([subst(sol[1][1],w(x)/R),subst(sol[1][2],w(x)/R),subst(sol[2][1],v(x)/R),subst(sol[2][2],v(x)/R)]/(q[T]*R^3/6/EI)); | |||
plot2d([[parametric, ξ, toPlot[1], [ξ,0,1]], | |||
[parametric, 1+ξ*subst(params,h[2]/h[1]), toPlot[2], [ξ,0,1]], | |||
[parametric, ξ, toPlot[3], [ξ,0,1]], | |||
[parametric, 1+ξ*subst(params,h[2]/h[1]), toPlot[4], [ξ,0,1]]], | |||
[legend, "w(x), sec 1", "w(x), sec 2", "v(x), sec 1", "v(x), sec 2"], | |||
[xlabel, "x/h_1->"],[ylabel, "w(x)/W_0, v(x)/V_0 ->"])$ | |||
toPlot: ratsimp([subst(sol[1][1],M[y](x)),subst(sol[1][2],M[y](x)),subst(sol[2][1],M[z](x)),subst(sol[2][2],M[z](x))]/(q[T]*R^2)); | |||
plot2d([[parametric, ξ, toPlot[1], [ξ,0,1]], | |||
[parametric, 1+ξ*subst(params,h[2]/h[1]), toPlot[2], [ξ,0,1]], | |||
[parametric, ξ, toPlot[3], [ξ,0,1]], | |||
[parametric, 1+ξ*subst(params,h[2]/h[1]), toPlot[4], [ξ,0,1]]], | |||
[legend, "M_y(x), sec 1", "M_y(x), sec 2", "M_z(x), sec 1", "M_z(x), sec 2"], | |||
[xlabel, "x/h_1->"],[ylabel, "M(x)/M_0 ->"])$ | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
Aktuelle Version vom 15. September 2022, 13:55 Uhr
Aufgabenstellung
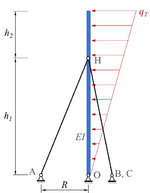
Das skizzierte System ist ein Mast unter einer linear veränderlichen Windlast, der durch drei gleichmäßig über den Umfang verteilten Stäbe abgestützt wird.
Gesucht ist die analytische Lösung für ein Euler-Bernoulli-Modell des elastischen Mastes und der drei Dehnstäbe.
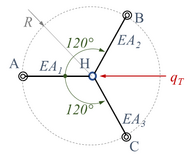
Der Mast steht senkrecht dabei auf einer ebenen Unterlage mit dem festen Gelenklager „O“ und ist durch drei Stäbe abgestützt. Alle Stäbe sind in Punkt „H“ mit dem Mast verbunden und in den Punkten „A“, „B“ und „C“ gelenkig gelagert. Die Lager A, B und C sind gleichmäßig in einem Radius von R um O herum auf der Unterlage verteilt. Die Windlast hat den Maximalwert qT und wirkt in der Ebene, die durch die Punkte A, O und H aufgespannt werden. Für die Geometrie des Masts gilt h1 = 2 h2, h2 = √2 R, außerdem sei die Dehnsteifigkeiten der Stäbe E A2=2 E A1,E A3=E A1.
Der Mast hat ein zylindrisches Profil mit Innen- und Außendurchmesser di, da.
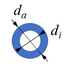
Ein Knicken der drei Stäbe sei ausgeschlossen.
Lösung mit Maxima
Mit Maxima berechnen wir die allgemeine Lösung der Differentialgleichung des Euler-Bernoulli-Balkens und geben die Rand- und Übergangsbedingungen an. Der Mast soll in Längsrichtung nicht signifikant durch die Stabkräfte verformt werden, als Koordinaten der Verschiebung haben hier also nur die Auslenkungen Querrichtung sowie die Verdrehungen um diese Koordinatenrichtungen. Die Stabkräfte berechnen wir aus der Längung der Stäbe, dabei linearisieren wir bezüglich der Mast-Auslenkungen.
Header
Kern der Lösung ist die Berechnung der Integrationskonstanten des Euler-Bernoulli-Balkens. In diesem Beispiel führen wir zusätzliche Abkürzungen als Variablen ein, um die Rand- und Übergangsbedingungen einfacher formulieren zu können.
/*******************************************************/
/* MAXIMA script */
/* version: wxMaxima 21.05.2 */
/* author: Andreas Baumgart */
/* last updated: 2022-08-19 */
/* ref: NMM, Labor 1 */
/* Mast unter linear-veränderlicher Windlast */
/* */
/*******************************************************/
Declarations
Wir übernehmen die Parameter aus der Aufgabenstellung, also
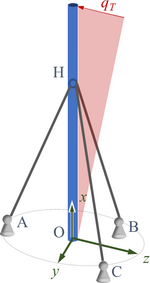
und definieren für die Berechnung der Stabkräfte die Referenzorte von A, B, C und H wie rechts skizziert im x, y, z Koordinatensystem zu
Die Koordinaten der Vektoren, die jeweils in Stablängsrichtung von H zu den Lagerpunkten zeigen, sind dann
die Referenz-Länge aller drei Stäbe ist damit
- .
Und wir schreiben damit die Koordinaten der Einheitsvektoren dieser Stab-Längsrichtungen als
- .
/*******************************************************/
/* declarations */
/* *****************************************************/
/* parameter selection */
params: [EA[2]=2*EA[1],EA[3]=EA[1], h[1] = 2*h[2], h[2]=sqrt(2)*R, EA[1] = α*EI/R^2];
assume(R>0);
/* non-sclar variables */
declare(r,nonscalar,
e,nonscalar);
/* geometry **********************************/
/* points */
geo: [r[H] = matrix([ h[1], 0, 0]),
r[A] = matrix([ 0 , R*sin( 0 ),-R*cos( 0 )]),
r[B] = matrix([ 0 , R*sin(-2*%pi/3),-R*cos(-2*%pi/3)]),
r[C] = matrix([ 0 , R*sin(+2*%pi/3),-R*cos(+2*%pi/3)])];
geo: append(geo, subst(geo, [r[1] = r[A]-r[H],
r[2] = r[B]-r[H],
r[3] = r[C]-r[H]]));
geo: append(geo, [L = sqrt(subst(geo,r[1]).subst(geo,r[1]))]);
/* unit-vecotor coefficients */
geo: append(geo, makelist(e[i]=subst(geo,r[i]/L),i,1,3));
Integration Of Differential Equation for Euler-Bernoulli-Beam
In den Bereichen I und II haben wir jeweils eine Auslenkung des Masts in zwei Richtungen: z und y.
Wir nutzen die Standard-Nomenklatur für den Euler-Bernoulli-Balken und schrieben jeweils die Gleichgewichtsbedingungen
| ... in z-Richtung als | ... in y-Richtung als | |
|---|---|---|
| . | . | |
|
Für die Auslenkungen in z und y-Richtung geben wir hier die Bedeutung der Koordinaten vi(x), wi(x) je Bereich und deren Ableitungen an. Es ist | ||
| ... die Querschnitts-Auslenkung: | ||
| ... die Querschnitts-Verdrehung: | ||
| ... das Biege-Moment: | und | |
| ... die Querkraft: | ||
Für die Streckenlasten auf den Mast gilt je Bereich "i" die lineare Funktion:
- ... in z-Richtung: und
- ... in y-Richtung:
wobei an den Knotenpunkten dies gilt:
Mit diesen Ansätzen erhalten wir aus der Integration der Differentialbeziehung für den Euler-Bernoulli-Balken diese generischen (weil mit Integrationskonstanten behaftete) Lösungen:
| Richung ... | z | y |
|---|---|---|
| Bereich I: | ||
| Bereich II: |
Wir haben also Bereich I und II für Richtungen z und y mit jeweils 4 integrationskonstanten - das macht insgesamt 16 zu bestimmende Variablen.
/*******************************************************/
/* differential equations for EB-beam */
/* and generic solution */
/* *****************************************************/
dgl: diff(w(x),x,4)=-1/EI*(q[i-1]*(1-x/h[i])+q[i]*x/h[i]);
dgl: integrate(integrate(integrate(integrate(dgl,x),x),x),x);
sectionReplace: [[%c1=c[ 1],%c2=c[ 2],%c3=c[ 3],%c4=c[ 4], q[i-1]= 0 , q[i]=q[H],h[i]=h[1] ],
[%c1=c[ 9],%c2=c[10],%c3=c[11],%c4=c[12], q[i-1]=q[H], q[i]=q[T],h[i]=h[2] ],
[%c1=c[ 5],%c2=c[ 6],%c3=c[ 7],%c4=c[ 8], q[i-1]= 0 , q[i]= 0 ,h[i]=h[1], w(x)=v(x)],
[%c1=c[13],%c2=c[14],%c3=c[15],%c4=c[16], q[i-1]= 0 , q[i]= 0 ,h[i]=h[2], w(x)=v(x)]];
/* create 4 lists for each section */
sol: [makelist(subst(sectionReplace[i],[dgl]),i,1,2),
makelist(subst(sectionReplace[i],[dgl]),i,3,4)];
sol: subst([q[H] = q[T]*h[1]/(h[1]+h[2])],sol);
/* tilt-angles, bending and cross-sec. force */
/* see Gross e.a.: Technische Mechanik 2, p156 */
for dir:1 thru 2 do
for sec:1 thru 2 do
(sol[dir][sec]: append(sol[dir][sec], [[ φ(x) , ψ(x) ][dir] = diff(subst(sol[dir][sec],[w(x),v(x)][dir]),x )]),
sol[dir][sec]: append(sol[dir][sec], [[M[y](x),M[z](x)][dir] = [-1,+1][dir]*EI*diff(subst(sol[dir][sec],[w(x),v(x)][dir]),x,2)]),
sol[dir][sec]: append(sol[dir][sec], [[Q[z](x),Q[y](x)][dir] = [-1,-1][dir]*EI*diff(subst(sol[dir][sec],[w(x),v(x)][dir]),x,3)]));
Forces in Supporting Rods
Die Zugkräfte Si in den drei Dehnstäben erhalten wir aus der Stab-Längung , also
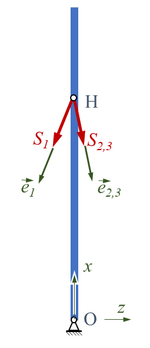
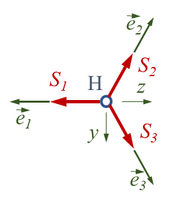
Die Bilder rechts zeigen die Stabkräfte am freigeschnittenen Punkt H des Masts. Bei der Berechnung der Stabkräfte ist die Längung von Stab i. Die Kraft hat als Richtung , also ist
- .
Es fehlt nur noch die Stablängung je Stab – und die bekommen wir aus dem Vergleich der Geometrie des Stabes im verformten und unverformten Zustand.
Analog zur Länge des Stabes im unverformten Zustand ist nun der Ort von H
und die Koeffizienten der Stab-Vektoren sind nun
- .
Die Differenzlänge erhalten wir – nach dem gleichen Schema wie oben – aus
- .
In
steht nun allerdings ein komplizierter, nichtlinearer Ausdruck. Den linearisieren wir, schreiben also
und erhalten damit
/*******************************************************/
/* forces S[i] in supporing rods */
/* S[i] as a function of W[H] and V[H] *****************/
/* *****************************************************/
ΔL: subst(geo,[r[A] - (r[H]+matrix([0,V[H],W[H]])),
r[B] - (r[H]+matrix([0,V[H],W[H]])),
r[C] - (r[H]+matrix([0,V[H],W[H]]))]);
ΔL: makelist(sqrt(ΔL[i].ΔL[i])-subst(geo,L),i,1,3);
displ: [W[H],V[H]];
null : makelist(displ[i]=0,i,1,2);
/* linearize .... */
ΔL: sum(subst(null, diff(ΔL,displ[j]))*displ[j],j,1,2);
S : makelist(EA[i]*ΔL[i]/subst(geo,L),i,1,3);
Boundary- and Transition-Conditions
Aus der Lösung der Differentialgleichungen für zwei Raumrichtungen und zwei Bereiche haben wir 16 Integrationskonstanten, die wir bestimmen müssen. Hinzu kommen VH und WH für den Knoten H. Um hier konsistent zu sein, führen wir für die Knoten H und T – "Top", die Mastspitze – die Koordinaten der Auslenkung und Kippung der Querschnitte ein, also zusammen die 8 Knotenvariablen
| Richtung | z | y |
|---|---|---|
| Knoten T Auslenkung Kippwinkel | , | , |
| Knoten H Auslenkung Kippwinkel | , | , |
| Knoten 0 Auslenkung Kippwinkel | , | , |
In O hätten wir auch noch die Variablen und einführen könnten. Die sind allerdings identisch mit und .
Alle Unbekannten fassen wir nun in
zusammen.
Für diese 24 Unbekannten brauchen wir nun 24 Gleichungen – Geometriebedingungen und Kräfte-/Momentengleichgewichte.
... aus Rand "O"
Das gelenkige Lager in O erlaubt keine Verschiebung und es nimmt keine Momente auf. Daraus ergeben sich die Geometrischen Bedingungen:
und die Kraft- und Momenten-Randbedingungen:
... aus Übergang "H"
Geometrische Bedingungen:
Kraft- und Momenten-Randbedingungen: Hier wird es spannend: durch die drei Stäbe werden Kräfte eingeleitet,
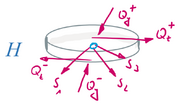
hier ohne Schnittmomente
Einfach sind die Momenten-Gleichgewichtsbedingungen am Knoten H - hier wird kein externes Moment eingeleitet, die beiden Schnittmomente müssen gleich sein:
Für die Kraft-Übergangsbedingungen in y- und z-Richtung müssen wir nun allerdings die Seilkräfte mit einbeziehen.
Dabei nehmen wir vom Einheitsvektor nur die Komponente der jeweiligen Raumrichtung, also z.B. aus .
... aus Rand "T"
Geometrische Bedingungen: Für die geometrischen Randbedingen haben wir nur die Gleichungen, die unsere Abkürzungen einführen, also
Kraft- und Momenten-Randbedingungen: Hier ist Rand frei: Kräfte und Momente in T müssen Null sein:
Damit sind wir komplett - wir haben 24 Gleichungen für 24 Unbekannte. Das Gleichungssystem können wir nun als
schreiben - oder mit den oben angegebenen Systemparametern ausgeschreiben als
/******************************************************/
/* Boundary Value Problem Formulation */
/* ****************************************************/
/* point "O" - geometry */
BC: [subst(x= 0 , subst(sol[1][1],w(x)) )= 0 ,
subst(x= 0 , subst(sol[2][1],v(x)) )= 0 ,
/* point "O" - bending moments */
subst(x= 0 , subst(sol[1][1],M[y](x)) )= 0 ,
subst(x= 0 , subst(sol[2][1],M[z](x)) )= 0 ,
/* point "H" - geometry */
subst(x= h[1], subst(sol[1][1],w(x)) )=W[H],
subst(x= h[1], subst(sol[2][1],v(x)) )=V[H],
subst(x= 0 , subst(sol[1][2],w(x)) )=W[H],
subst(x= 0 , subst(sol[2][2],v(x)) )=V[H],
subst(x= h[1], subst(sol[1][1],φ(x)) )=Φ[H],
subst(x= h[1], subst(sol[2][1],ψ(x)) )=Ψ[H],
subst(x= 0 , subst(sol[1][2],φ(x)) )=Φ[H],
subst(x= 0 , subst(sol[2][2],ψ(x)) )=Ψ[H],
/* point "H" - bending moments */
subst(x= h[1], subst(sol[1][1],M[y](x)) )=subst(x= 0 , subst(sol[1][2],M[y](x)) ),
subst(x= h[1], subst(sol[2][1],M[z](x)) )=subst(x= 0 , subst(sol[2][2],M[z](x)) ),
/* point "H" - forces */
subst(x= h[1], subst(sol[1][1],Q[z](x)) )=subst(x= 0 , subst(sol[1][2],Q[z](x)) ) + sum(S[i]*subst(geo,e[i]),i,1,3)[1][3],
subst(x= h[1], subst(sol[2][1],Q[y](x)) )=subst(x= 0 , subst(sol[2][2],Q[y](x)) ) + sum(S[i]*subst(geo,e[i]),i,1,3)[1][2],
/* point "T" (Top) - geometry */
subst(x= h[2], subst(sol[1][2],w(x)) )=W[T],
subst(x= h[2], subst(sol[2][2],v(x)) )=V[T],
subst(x= h[2], subst(sol[1][2],φ(x)) )=Φ[T],
subst(x= h[2], subst(sol[2][2],ψ(x)) )=Ψ[T],
/* point "T" (Top) - bending moment */
subst(x= h[2], subst(sol[1][2],M[y](x)) ) = 0,
subst(x= h[2], subst(sol[2][2],M[z](x)) ) = 0,
/* point "T" (Top) - forces */
subst(x= h[2], subst(sol[1][2],Q[z](x)) ) = 0,
subst(x= h[2], subst(sol[2][2],Q[y](x)) ) = 0];
C: append(makelist(c[i],i,16), [W[H],V[H],Φ[H],Ψ[H],W[T],V[T],Φ[T],Ψ[T]]);
scale: [1,1,1,1,1,1,1,1,1,1,
1,1,EI,EI,EI,EI,1,1,1,1,
EI,EI,EI,EI];
for i:1 thru 24 do BC[i]:BC[i]/scale[i];
ACM: ratsimp(augcoefmatrix(BC,C));
a: submatrix(ACM,25);
b:-col(ACM,25);
Solving
Dieses lineare Gleichungssystem kann man gerade noch analytisch lösen - wir finden die gesuchten Integrationskonstanten und Knotenvariablen
/*******************************************************/
/* solve for integration constants */
/* *****************************************************/
consts: ratsimp(solve(ratsimp(subst(params,BC)),C)[1]);
sol: subst(consts,sol);
toReplace: [x=ξ*h[1],x=ξ*h[2]];
for dir: 1 thru 2 do
for sec: 1 thru 2 do
(print(dir,sec),
for elem: 1 thru 4 do
sol[dir][sec][elem]: lhs(sol[dir][sec][elem])=subst(toReplace[sec],rhs(sol[dir][sec][elem])));
Post-Processing
Die Verläufe der Auslenkung und Schnittkräfte - hier exemplarisch das Biegemoment - können wir nun plotten:
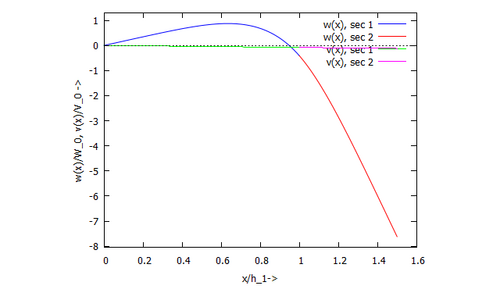 |  |
/*******************************************************/
/* post-processing */
/*******************************************************/
/* what is a reasonable size is α ? */
/* geopar: [A[1]= π/ 4*d[r]^2, d[r]=1*cm,
I = π/64*(d[o]^4-d[i]^4), d[o]=10*cm, d[i]=9*cm,
R = h[2]/sqrt(2), h[2]=500*cm,
α = A[1]*R^2/I ] */
sol: ratsimp(subst([α=500],subst(params,sol)));
toPlot: ratsimp([subst(sol[1][1],w(x)/R),subst(sol[1][2],w(x)/R),subst(sol[2][1],v(x)/R),subst(sol[2][2],v(x)/R)]/(q[T]*R^3/6/EI));
plot2d([[parametric, ξ, toPlot[1], [ξ,0,1]],
[parametric, 1+ξ*subst(params,h[2]/h[1]), toPlot[2], [ξ,0,1]],
[parametric, ξ, toPlot[3], [ξ,0,1]],
[parametric, 1+ξ*subst(params,h[2]/h[1]), toPlot[4], [ξ,0,1]]],
[legend, "w(x), sec 1", "w(x), sec 2", "v(x), sec 1", "v(x), sec 2"],
[xlabel, "x/h_1->"],[ylabel, "w(x)/W_0, v(x)/V_0 ->"])$
toPlot: ratsimp([subst(sol[1][1],M[y](x)),subst(sol[1][2],M[y](x)),subst(sol[2][1],M[z](x)),subst(sol[2][2],M[z](x))]/(q[T]*R^2));
plot2d([[parametric, ξ, toPlot[1], [ξ,0,1]],
[parametric, 1+ξ*subst(params,h[2]/h[1]), toPlot[2], [ξ,0,1]],
[parametric, ξ, toPlot[3], [ξ,0,1]],
[parametric, 1+ξ*subst(params,h[2]/h[1]), toPlot[4], [ξ,0,1]]],
[legend, "M_y(x), sec 1", "M_y(x), sec 2", "M_z(x), sec 1", "M_z(x), sec 2"],
[xlabel, "x/h_1->"],[ylabel, "M(x)/M_0 ->"])$
Links
- ...
Literature
- ...