Gelöste Aufgaben: Unterschied zwischen den Versionen
KKeine Bearbeitungszusammenfassung |
KKeine Bearbeitungszusammenfassung |
||
| (12 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 14: | Zeile 14: | ||
Bitte orientieren Sie sich an den [[Spezial:Kategorien|Schlagworten]] (Tags) auf der [[Hauptseite|Startseite]], wenn Sie Aufgaben zu bestimmten Themen suchen. | Bitte orientieren Sie sich an den [[Spezial:Kategorien|Schlagworten]] (Tags) auf der [[Hauptseite|Startseite]], wenn Sie Aufgaben zu bestimmten Themen suchen. | ||
A ∙ B ∙ [[#C|C]] ∙ [[#D|D]] ∙ E ∙ [[#F|F]] ∙ [[#G|G]] ∙ [[#H|H]] ∙ I ∙ [[#J|J]] ∙ [[#K|K]] ∙ [[#L|L]] ∙ M ∙ N ∙ [[#O|O]] ∙ [[#P|P]] ∙ Q ∙ R ∙ [[#S|S]] ∙ [[#T|T]] ∙ [[#U|U]] ∙ V ∙ [[#W|W]] ∙ X ∙ Y ∙ Z | A ∙ [[#B|B]] ∙ [[#C|C]] ∙ [[#D|D]] ∙ E ∙ [[#F|F]] ∙ [[#G|G]] ∙ [[#H|H]] ∙ I ∙ [[#J|J]] ∙ [[#K|K]] ∙ [[#L|L]] ∙ [[#M|M]] ∙ N ∙ [[#O|O]] ∙ [[#P|P]] ∙ Q ∙ R ∙ [[#S|S]] ∙ [[#T|T]] ∙ [[#U|U]] ∙ V ∙ [[#W|W]] ∙ X ∙ Y ∙ Z | ||
<span id="B"/> | |||
{{Vorlage:MySolvedProblem|id=Bike|excerpt={{:Gelöste_Aufgaben/Bike}}}} | |||
{{Vorlage:MySolvedProblem|id=Buck|excerpt={{:Gelöste_Aufgaben/Buck}}}} | |||
<span id="C"/> | <span id="C"/> | ||
{{Vorlage:MySolvedProblem|id=COVI|excerpt={{:Gelöste_Aufgaben/COVI}}}} | {{Vorlage:MySolvedProblem|id=COVI|excerpt={{:Gelöste_Aufgaben/COVI}}}} | ||
| Zeile 35: | Zeile 38: | ||
{{Vorlage:MySolvedProblem|id=FEB3|excerpt={{:Gelöste_Aufgaben/FEB3}}}} | {{Vorlage:MySolvedProblem|id=FEB3|excerpt={{:Gelöste_Aufgaben/FEB3}}}} | ||
{{Vorlage:MySolvedProblem|id=FEB4|excerpt={{:Gelöste_Aufgaben/FEB4}}}} | {{Vorlage:MySolvedProblem|id=FEB4|excerpt={{:Gelöste_Aufgaben/FEB4}}}} | ||
{{Vorlage:MySolvedProblem|id=FEC0|excerpt={{:Gelöste_Aufgaben/FEC0}}}} | |||
{{Vorlage:MySolvedProblem|id=FEC1|excerpt={{:Gelöste_Aufgaben/FEC1}}}} | {{Vorlage:MySolvedProblem|id=FEC1|excerpt={{:Gelöste_Aufgaben/FEC1}}}} | ||
{{Vorlage:MySolvedProblem|id=FEM1|excerpt={{:Gelöste_Aufgaben/FEM1}}}} | {{Vorlage:MySolvedProblem|id=FEM1|excerpt={{:Gelöste_Aufgaben/FEM1}}}} | ||
<span id="G"/> | <span id="G"/> | ||
{{Vorlage:MySolvedProblem|id=GYRO|excerpt={{:Gelöste_Aufgaben/GYRO}}}} | {{Vorlage:MySolvedProblem|id=GYRO|excerpt={{:Gelöste_Aufgaben/GYRO}}}} | ||
{{Vorlage:MySolvedProblem|id=GYRQ|excerpt={{:Gelöste_Aufgaben/GYRQ}}}} | |||
<span id="H"/> | <span id="H"/> | ||
{{Vorlage:MySolvedProblem|id=Hko8|excerpt={{:Gelöste_Aufgaben/Hko8}}}} | {{Vorlage:MySolvedProblem|id=Hko8|excerpt={{:Gelöste_Aufgaben/Hko8}}}} | ||
| Zeile 49: | Zeile 54: | ||
{{Vorlage:MySolvedProblem|id=Kit5|excerpt={{:Gelöste_Aufgaben/Kit5}}}} | {{Vorlage:MySolvedProblem|id=Kit5|excerpt={{:Gelöste_Aufgaben/Kit5}}}} | ||
{{Vorlage:MySolvedProblem|id=Kit6|excerpt={{:Gelöste_Aufgaben/Kit6}}}} | {{Vorlage:MySolvedProblem|id=Kit6|excerpt={{:Gelöste_Aufgaben/Kit6}}}} | ||
{{Vorlage:MySolvedProblem|id=Kita|excerpt={{:Gelöste_Aufgaben/Kita}}}} | |||
{{Vorlage:MySolvedProblem|id=Kitb|excerpt={{:Gelöste_Aufgaben/Kitb}}}} | |||
{{Vorlage:MySolvedProblem|id=Kv52|excerpt={{:Gelöste_Aufgaben/Kv52}}}} | {{Vorlage:MySolvedProblem|id=Kv52|excerpt={{:Gelöste_Aufgaben/Kv52}}}} | ||
{{Vorlage:MySolvedProblem|id=Kv53|excerpt={{:Gelöste_Aufgaben/Kv53}}}} | {{Vorlage:MySolvedProblem|id=Kv53|excerpt={{:Gelöste_Aufgaben/Kv53}}}} | ||
| Zeile 72: | Zeile 79: | ||
{{Vorlage:MySolvedProblem|id=LA01|excerpt={{:Gelöste_Aufgaben/LA01}}}} | {{Vorlage:MySolvedProblem|id=LA01|excerpt={{:Gelöste_Aufgaben/LA01}}}} | ||
{{Vorlage:MySolvedProblem|id=LM01|excerpt={{:Gelöste_Aufgaben/LM01}}}} | {{Vorlage:MySolvedProblem|id=LM01|excerpt={{:Gelöste_Aufgaben/LM01}}}} | ||
<span id="M"/> | |||
{{Vorlage:MySolvedProblem|id=MaMa|excerpt={{:Gelöste_Aufgaben/MaMa}}}} | |||
<span id="O"/> | <span id="O"/> | ||
{{Vorlage:MySolvedProblem|id=ODE1|excerpt={{:Gelöste_Aufgaben/ODE1}}}} | {{Vorlage:MySolvedProblem|id=ODE1|excerpt={{:Gelöste_Aufgaben/ODE1}}}} | ||
| Zeile 81: | Zeile 90: | ||
{{Vorlage:MySolvedProblem|id=SKEB|excerpt={{:Gelöste_Aufgaben/SKEB}}}} | {{Vorlage:MySolvedProblem|id=SKEB|excerpt={{:Gelöste_Aufgaben/SKEB}}}} | ||
{{Vorlage:MySolvedProblem|id=SKER|excerpt={{:Gelöste_Aufgaben/SKER}}}} | {{Vorlage:MySolvedProblem|id=SKER|excerpt={{:Gelöste_Aufgaben/SKER}}}} | ||
{{Vorlage:MySolvedProblem|id=StaB|excerpt={{:Gelöste_Aufgaben/StaB}}}} | |||
{{Vorlage:MySolvedProblem|id=StaF|excerpt={{:Gelöste_Aufgaben/StaF}}}} | |||
{{Vorlage:MySolvedProblem|id=Stor|excerpt={{:Gelöste_Aufgaben/Stor}}}} | |||
<span id="T"/> | <span id="T"/> | ||
{{Vorlage:MySolvedProblem|id=T312|excerpt={{:Gelöste_Aufgaben/T312}}}} | {{Vorlage:MySolvedProblem|id=T312|excerpt={{:Gelöste_Aufgaben/T312}}}} | ||
{{Vorlage:MySolvedProblem|id=T313|excerpt={{:Gelöste_Aufgaben/T313}}}} | {{Vorlage:MySolvedProblem|id=T313|excerpt={{:Gelöste_Aufgaben/T313}}}} | ||
{{Vorlage:MySolvedProblem|id=T3BP|excerpt={{:Gelöste_Aufgaben/T3BP}}}} | |||
{{Vorlage:MySolvedProblem|id=T401|excerpt={{:Gelöste_Aufgaben/T401}}}} | {{Vorlage:MySolvedProblem|id=T401|excerpt={{:Gelöste_Aufgaben/T401}}}} | ||
{{Vorlage:MySolvedProblem|id=TC12|excerpt={{:Gelöste_Aufgaben/TC12}}}} | {{Vorlage:MySolvedProblem|id=TC12|excerpt={{:Gelöste_Aufgaben/TC12}}}} | ||
Aktuelle Version vom 28. Dezember 2025, 06:51 Uhr
Die Liste von Aufgaben auf dieser Seite ist nicht thematisch sortier. Die Seiten-Titel (z.B. FEAG) sind lediglich eindeutige Kennungen - sie haben keine inhaltliche Bedeutung.
Das explizite Lösungsschema für die Bearbeitung der Aufgaben orientiert sich nach einem festen Muster. Grundsätzlich folgen wir dem Standardprozess der Modellbildung. Die meisten Aufgaben sind dafür allerdings zu "klein" und wir adaptieren ein "passendes" Schema.
Quellcode
Zu jeder Lösung einer Aufgabe gibt es abschnittsweise den Quellcode - über die Code-Page-Icons (rechts →) kann er aus- oder eingeklappt werden.
/* this is Maxima-code */
equation: 1+1=2;
Bitte orientieren Sie sich an den Schlagworten (Tags) auf der Startseite, wenn Sie Aufgaben zu bestimmten Themen suchen.
A ∙ B ∙ C ∙ D ∙ E ∙ F ∙ G ∙ H ∙ I ∙ J ∙ K ∙ L ∙ M ∙ N ∙ O ∙ P ∙ Q ∙ R ∙ S ∙ T ∙ U ∙ V ∙ W ∙ X ∙ Y ∙ Z
Bike | |
 |
Buck | |
 Gesucht sind die Ansätze für die Berechnung der kritischen Drucklast, ausgehend von
|
COVI | |
 Gesucht ist hier ein phänomenologisches Modell für die Entwicklung der Anzahl der Individuen, die
|
DGEB | |
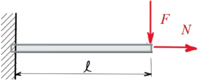 Gesucht sind die Differentialgleichungen des statischen Gleichgewichts für den schlanken Stab mit Rechteck-Querschnitt unter Längs- und Querkraft, ausgehend von der Virtuellen Formänderungsenergie δΠ. Wir finden so die bekannten Differentialbeziehungen für das Timoshenko / Euler-Bernoulli-Modell eines Balkens. |
DGEC | |
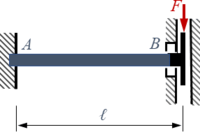 Ein Balken AB (Länge ℓ, Rechteck-Querschnitt h*b, Elastizitäts-Module E) ist in A fest eingespannt und in B durch eine Parallelführung gelagert. In B wird er durch eine senkrechte Kraft F belastet. Wir vergleichen die Auslenkung in B nach den Balken-Modellen von |
FEAA | |
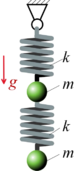 |
FEAB | |
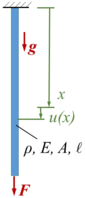 |
FEAC | |
 |
FEAD | |
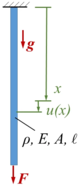 |
FEAE | |
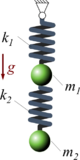 |
FEAF | |
 Gesucht ist die Längsschwingung des Stabes beim Loslassen aus seiner unverformten Referenzlage. Dabei arbeiten wir mit der Methode der Finiten Elemente zum Aufstellen der Bewegungsgleichungen. Die Integeationskonstanten der Lösung passen wir an die Anfangsbedingungen
|
FEAG | |
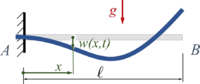 |
FEB1 | |
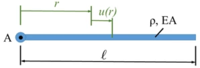 Ein Hubschrauber-Rotor dreht mir der konstanten Winknelgeschwindigkeit Ω. Das Rotor-Blatt ist aus Aluminium. Gesucht ist die FEM-Lösung für der Verschiebung der Querschnitte und die Dehnung der Querschnitte. |
FEB2 | |
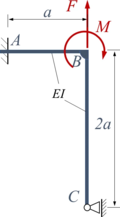 |
FEB3 | |
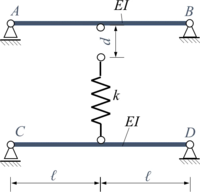 |
FEB4 | |
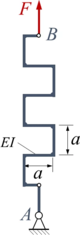 Das skizzierte System besteht aus Euler-Bernoulli-Balken (jeweils Länge a) der Biegesteifigkeit EI. Die Konstruktion wird in A durch ein gelenkiges Festlager gehalten und in B durch die Kraft F belastet. Gesucht ist die Ersatzfeder-Steifigkeit des Systems, das Sie aus Finiten Elementen mit Euler-Bernoulli-Balken zusammensetzen. |
FEC0 | |
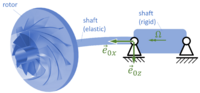 |
FEC1 | |
 |
FEM1 | |
 Using ANSYS workbench, decide upon the wall-thickness of a pressure-vessel subject to a differential internal pressure of p=1 bar. Let |
GYRO | |
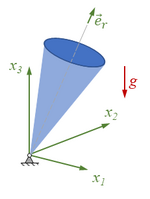 Gesucht ist die Präzessions-Bahn eines Kreisels mit Euler-Drehwinklen. Unser Kreisel ist ein Kegel der Höhe H und Radius R. Die Bewegungsgleichungen sollen mit dem Prinzip der virtuellen Verrückungen aufgestellt werden. Wir suchen nach der Trajektorie des Mittelpunktes des Kreisels für große Kippwinkel. |
GYRQ | |
 Gesucht ist die Präzessions-Bahn eines Kreisels mit Quaternionen / Kugelkoordinaten. Unser Kreisel ist ein Kegel der Höhe H und Radius R. Die Bewegungsgleichungen sollen mit dem Prinzip der virtuellen Verrückungen aufgestellt werden. Wir suchen nach der Trajektorie des Mittelpunktes des Kreisels für große Kippwinkel. |
Hko8 | |
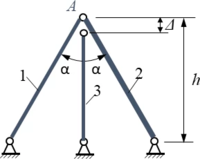 Drei Stäbe 1, 2 und 3 werden in Punkt A verbunden. Aufgrund einer Fertigungstoleranz ist Stab 3 um zu kurz. Gesucht ist die Verschiebung des Punktes A nach dem Einhängen von Stab 3 sowie die Spannungen in den Stäben. |
JUMP | |||
Create a mathematical Model for an RC-Model Car. The model shall account for the basic car-functions in a 2D-driving environment including vehicle dynamics, drive-train, battery and driver. A 2D-test-parkour shall be provided to assess basic climbing and jumping capabilities of the car. |
Kerb | |
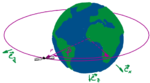 Ein Satellit soll eine stabile Umlaufbahn um die Erde beschreiben. Gesucht sind mögliche Lösungen. |
Kig1 | |
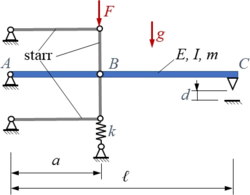 Damit der Schalter zuverlässig funktioniert soll die Kraft F an der Führung so gewählt werden, dass die vorgegebene Kontaktkraft K eingestellt wird. Gesucht ist die analytische Lösung für ein Euler-Bernoulli-Modell der elastischen Struktur. |
Kit4 | |
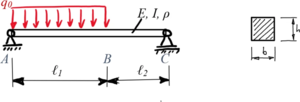 |
Kit5 | |
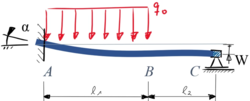 |
Kit6 | |
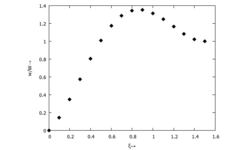 |
Kita | |
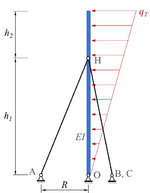 Das skizzierte System ist ein Mast unter einer linear veränderlichen Windlast, der durch drei gleichmäßig über den Umfang verteilten Stäbe abgestützt wird. Gesucht ist die analytische Lösung für ein Euler-Bernoulli-Modell des elastischen Mastes und der drei Dehnstäbe. |
Kitb | |
 Das skizzierte System ist ein Mast unter einer linear veränderlichen Windlast, der durch drei gleichmäßig über den Umfang verteilten Stäbe abgestützt wird. Gesucht ist die Näherungslösung für ein FE-Modell des Masts (Euler-Bernoulli-Balken) und der drei Dehnstäbe. |
Kv52 | |
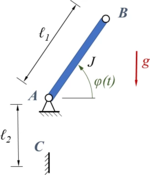 Ein starrer Stab AB (Massenmoment JA, Länge ℓ1) wird aus dem Winkel φ0 im Erdschwerefeld losgelassen und stößt in C auf einen Anschlag. Der Stoß zwischen Stab und Oberfläche sei ideal-elastisch. Gesucht ist die nichtlineare Bewegungsgleichung und die numerische Lösung als Anfangswertproblem. |
Kv53 | |
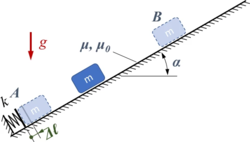 |
Kw23 | |
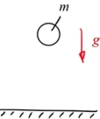 |
Kw24 | |
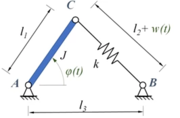 |
Kw25 | |
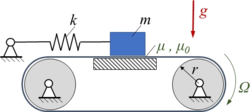 |
Kw26 | |
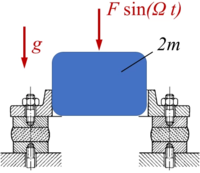 Für dieses System mit einem nichtlineares Federelement soll die Lösung als Anfangswertproblem gefunden und mit der linearen Näherungslösung verglichen werden. Gesucht sind
|
Kw27 | |
 |
Kw28 | |
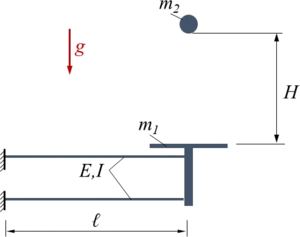 Für das skizzierte System modellieren Sie die Kugel als elastisch, die elastisch gelagerte Plattform als starr. Gesucht ist eine numerische Lösung als Anfangswertproblem und die nichtlinearen Schwingungen der beiden Systemteile. |
Kw29 | |
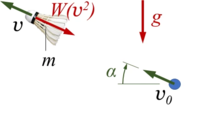 |
Kw30 | |
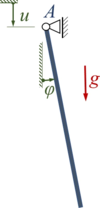 Das Pendel der Masse m und Länge ℓ der Aufgabe hat einen in A senkrecht mit u(t) periodisch bewegten Aufhängepunkt. Berechnen Sie die Stabilität der Lösung der linearisierten Bewegungsgleichung für verschiedene Parameterkombinationen. |
Kw50 | |
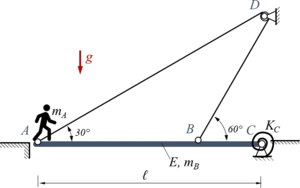 |
Kw51 | |
 Geben Sie die Lösung für ein Euler-Bernoulli-Modell der Brücke mit dem Verfahren von Rayleigh-Ritz (EBB) an - hier mit Lagrange-Multiplikator für die geometrische Zwangsbedingung. Dies ist eine Näherungslösung zu Kw50. |
Kw52 | |
 Geben Sie die Lösung für ein Euler-Bernoulli-Modell der Brücke mit dem Ansatz der Finiten Elemente an. Dies ist eine Näherungslösung zu Kw50. |
Kw53 | |
 Geben Sie die Lösung für ein Euler-Bernoulli-Modell der Brücke mit dem Verfahren von Rayleigh-Ritz (EBB) an - hier ohneLagrange-Multiplikator für die geometrische Zwangsbedingung. Dies ist eine Näherungslösung zu Kw50. |
Kw55 | |
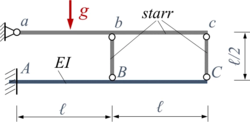 |
Kw56 | |
 |
Kw60 | |
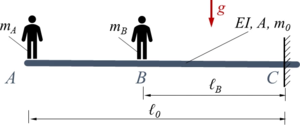 Gesucht ist eine Näherungslösung mit der Methode der Finiten Elemente und zwei Elementen. Dabei sollen die Verläufe der Biegelinie und die Schnittlasten mit der analytischen Lösung verlglichen werden. |
Kw96 | |
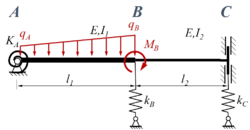 |
Kw98 | |
 |
Kw99 | |
 |
LA01 | |
 Eine Maschine produziert die Werkstücke "a" und "b" in einer 8h-Schicht. Die Anzahl der produzierten Werkstücke ist gegeben. Die Rüstzeit für beide Werkstücke an der Maschine sei gleich. Gesucht ist die Bearbeitungsdauern jeweils für Werkstück a und b. |
LM01 | |
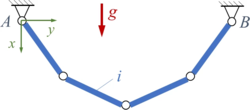 |
MaMa | |
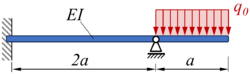 |
ODE1 | |
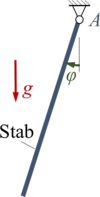 |
PvV1 | |
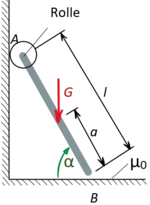 |
PvV2 | |
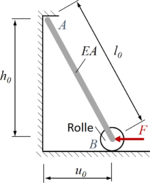 |
SKEB | |
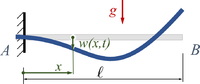 |
SKER | |
 |
StaB | |
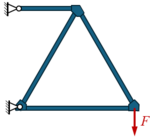 |
StaF | |
 |
Stor | |
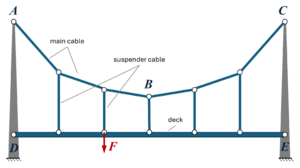 Gesucht ist ein einfaches, lineares FE-Modell für statische Spannungen und Verformungen der Seile und Fahrbahn. Die Verformung der Pylone soll icht berücksichtigt werden. |
T312 | |
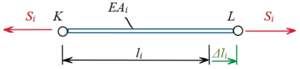 |
T313 | |
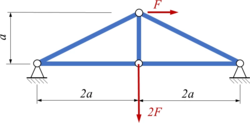 |
T3BP | |
Wir untersuchen das „Three-Body-Problem“(vgl. Wikipedia) numerisch. Dabei sollen die Bahnen von drei Körper mit den Punktmassen m1, m2, m3 in Wechselwirkung miteinander berechnet werden.
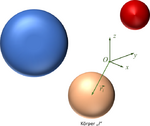 |
T401 | |
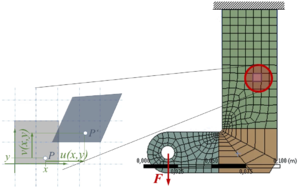 Bei der Analyse eines ebenen Bauteils wird der Verschiebungszustand eines Finiten Elementes durch erfasst. Gesucht sind die Hauptspannungen und Hauptspannungs-Richtungen im Finiten Element. |
TC12 | |
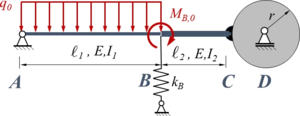 |
TC13 | |
 |
TkPb | |
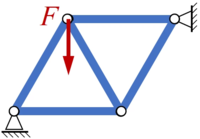 |
Tzul | |
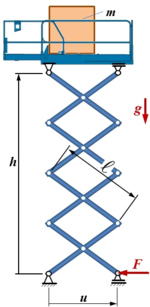 Auf der skizzierten Scherenbühne mit Stablänge ℓ steht eine Masse m. Berechnen Sie die Kraft F als Funktion der Höhe h. |
UEBA | |
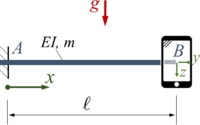 Für den Versuch wird der Balken wird durch seine Gewichtskraft belastet. Er ist in A fest eingespannt, die Masse des Smartphones sei vernachlässigbar. Gesucht ist die Lösung mit dem Ansatz von Rayleigh-Ritz und zwei Trial-Functions. |
UEBB | |
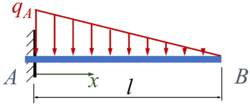 Der Euler-Bernoulli-Balken AB wird durch eine linear veränderliche Streckenlast belastet. Gesucht ist die Lösung für w(x) mit dem Ansatz von Ritz und zwei Trial-Functions. |
UEBC | |
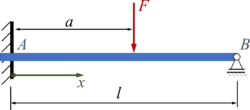 |
UEBD | |
 |
UEBF | |
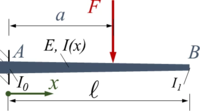 |
UEBH | |
Der Euler-Bernoulli-Balken AB wird durch ein Moment M zwischen den beiden gelenkigen Lagern belastet.
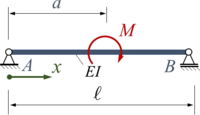 |
UEBI | |
 |
UEBJ | |
 |
UEBK | |
 |
UEBL | |
 |
UEBO | |
 Gesucht ist eine Lösung für die Biegelinie mit dem Ansatz von Ritz und zwei Trial-Funktionen. (Weg "1" wie in UEBH beschrieben.) |
UEBP | |
 |
W8Zt | |
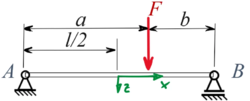 |
W8Zu | |
 |
W8Zv | |
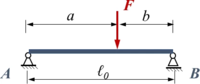 Hier soll mit dem Ansatz mit der Methode der Finiten Elemente gearbeitet werden. Gesucht ist das Verschiebungsfeld w(x) im Vergleich von FEM und analytischer Lösung. |
- Bike
- Buck
- COVI
- DGEB
- DGEC
- FEAA
- FEAB
- FEAC
- FEAD
- FEAE
- FEAF
- FEAG
- FEB1
- FEB2
- FEB3
- FEB4
- FEC0
- FEC1
- FEM1
- GYRO
- GYRQ
- Hko8
- JUMP
- Kerb
- Kig1
- Kit4
- Kit5
- Kit6
- Kita
- Kitb
- Kv52
- Kv53
- Kw23
- Kw24
- Kw25
- Kw26
- Kw27
- Kw28
- Kw29
- Kw30
- Kw50
- Kw51
- Kw52
- Kw53
- Kw55
- Kw56
- Kw60
- Kw96
- Kw98
- Kw99
- LA01
- LM01
- MaMa
- ODE1
- ODE2
- PvV1
- PvV2
- SKEB
- SKER
- StaB
- StaF
- Stor
- T312
- T313
- T3BP
- T3PB
- T401
- TC12
- TC13
- TkPb
- Tzul
- UEBA
- UEBB
- UEBC
- UEBD
- UEBF
- UEBH
- UEBI
- UEBJ
- UEBK
- UEBL
- UEBO
- UEBP
- W8Zt
- W8Zu
- W8Zv
- template