Gelöste Aufgaben/W8Zt: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| (Eine dazwischenliegende Version desselben Benutzers wird nicht angezeigt) | |||
| Zeile 11: | Zeile 11: | ||
<onlyinclude> | <onlyinclude> | ||
[[Datei: | [[Datei:W8Zt-01.png|250px|left|mini|Caption]] | ||
Gesucht ist eine Lösung in Anlehnung an das Verfahren von Ritz - bei dem wir mit Formfunktionen arbeiten, die sich über die gesamte Balkenlänge erstrecken, wir aber im dann mit dem Prinzip der virtuellen Verrückungen arbeiten. | Gesucht ist eine Lösung in Anlehnung an das Verfahren von Ritz - bei dem wir mit Formfunktionen arbeiten, die sich über die gesamte Balkenlänge erstrecken, wir aber im dann mit dem Prinzip der virtuellen Verrückungen arbeiten. | ||
</onlyinclude> | </onlyinclude> | ||
Üblich ist bei [[Randwertprobleme/Methoden zur Lösung von Randwertproblemen/Im Vergleich: das Verfahren von Ritz und die Methode der Finite Elemente|Verfahren von Rayleigh-Ritz]] nämlich sonst das [[Werkzeuge/Gleichgewichtsbedingungen/Arbeitsprinzipe der Analytischen Mechanik/Prinzip vom Minimum der Potentiellen Energie|Prinzip vom Minimum der Potentiellen Energie]]. | |||
Üblich ist bei [[Randwertprobleme/Methoden zur Lösung von Randwertproblemen/Im Vergleich: das Verfahren von Ritz und die Methode der Finite Elemente|Verfahren von Rayleigh-Ritz]] nämlich sonst das [[Werkzeuge/Gleichgewichtsbedingungen/Arbeitsprinzipe der Analytischen Mechanik/Prinzip vom Minimum der Potentiellen Energie|Prinzip vom Minimum der Potentiellen Energie]]. Die Lösung nach dem Standardverfahren finden Sie hier in [[Gelöste Aufgaben/W8Zu|W8Zu]]. | |||
== Lösung mit Maxima == | == Lösung mit Maxima == | ||
Mit dem [[Sources/Lexikon/Föppl-Symbol|Föppl-Symbol "<>"]], | Mit dem [[Sources/Lexikon/Föppl-Symbol|Föppl-Symbol "<>"]], sowie | ||
::<math>\alpha = a/\ell</math>, <math>\beta = 1-\alpha</math> und <math>\xi = x/\ell</math> | ::<math>\alpha = a/\ell</math>, <math>\beta = 1-\alpha</math> und <math>\xi = x/\ell</math> | ||
| Zeile 112: | Zeile 113: | ||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
1+1 | /**** define form functions ***/ | ||
/* coordinates */ | |||
coords : [[V,Psi], [δV,δΨ]]; | |||
/* generic polynomials */ | |||
define(v[1](x),sum(c[1,2*i]*x^(2*i),i,0,1)); | |||
define(v[2](x),sum(c[2,(2*i+1)]*x^(2*i+1),i,0,1)); | |||
/* solve for c's to comply with geometric boundary conditions */ | |||
coeffs : append(solve([v[1](0)=V,v[1](+l/2)=0],[c[1,0],c[1,2]])[1], | |||
solve([subst([x=0],diff(v[2](x),x))=Psi,v[2](+l/2)=0],[c[2,1],c[2,3]])[1]); | |||
/* employ in polynomials */ | |||
forms : [w(x) = expand(subst(coeffs, sum(v[i](x),i,1,2)))]; | |||
forms : append(forms, | |||
[δw(x) = subst(makelist(coords[1][i]=coords[2][i],i,1,2),subst(forms,w(x)))]); | |||
trials: subst([x=l*xi],makelist(coeff(subst(forms,w(x)), coords[1][i]),i,1,2)); | |||
plot2d( [trials[1],trials[2]/l],[xi,-1/2,+1/2], [legend, "φ[1]","φ[2]"]); | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
== | <!--------------------------------------------------------------------------------> | ||
{{MyCodeBlock|title=Equilibrium Conditions | |||
|text= | |||
Mit dem [[Werkzeuge/Gleichgewichtsbedingungen/Arbeitsprinzipe der Analytischen Mechanik/Prinzip der virtuellen Verrückungen|Prinzip der virtuellen Verrückungen]] ist die Gleichgewichtsbedingung immer | Mit dem [[Werkzeuge/Gleichgewichtsbedingungen/Arbeitsprinzipe der Analytischen Mechanik/Prinzip der virtuellen Verrückungen|Prinzip der virtuellen Verrückungen]] ist die Gleichgewichtsbedingung immer | ||
<math>\delta W=\delta A-\delta \Pi</math> | ::<math>\delta W=\delta A-\delta \Pi</math> | ||
Mit den Beiträgen | Mit den Beiträgen | ||
<math>\delta A=F\cdot \delta w\left( {{x}_{F}}\right) ,\delta\Pi=\int_{-\frac{\ell}{2}}^{\frac{\ell}{2}}\left( \frac{{{d}^{2}}}{d\,{{x}^{2}}}\cdot w\left( x\right) \right) \cdot \left( \frac{{{d}^{2}}}{d\,{{x}^{2}}}\cdot \delta w \left( x\right) \right) dx\cdot EI</math> | ::<math>\delta A=F\cdot \delta w\left( {{x}_{F}}\right) ,\delta\Pi=\int_{-\frac{\ell}{2}}^{\frac{\ell}{2}}\left( \frac{{{d}^{2}}}{d\,{{x}^{2}}}\cdot w\left( x\right) \right) \cdot \left( \frac{{{d}^{2}}}{d\,{{x}^{2}}}\cdot \delta w \left( x\right) \right) dx\cdot EI</math> | ||
und dem Einsetzen der Ansatzfunktionen und deren Variation finden wir | und dem Einsetzen der Ansatzfunktionen und deren Variation finden wir | ||
<math>\begin{array}{ll}\delta W = & -\frac{\displaystyle \left( 64\cdot EI \cdot V+ ({{\alpha}^{2}}-1) \cdot {{\ell}^{3}}\cdot F\right)}{\displaystyle {\ell}^{3}} \cdot \delta V \\ &+ \frac{\displaystyle {{\ell}^{2}}\cdot \left( \alpha \cdot ({{\alpha}^{2}}-1) \cdot {{\ell}^{2}}\cdot F+96\cdot \Psi\cdot EI \right)}{\displaystyle 2\cdot {{\ell}^{3}}} \cdot \delta\Psi \end{array}</math> | ::<math>\begin{array}{ll}\delta W = & -\frac{\displaystyle \left( 64\cdot EI \cdot V+ ({{\alpha}^{2}}-1) \cdot {{\ell}^{3}}\cdot F\right)}{\displaystyle {\ell}^{3}} \cdot \delta V \\ &+ \frac{\displaystyle {{\ell}^{2}}\cdot \left( \alpha \cdot ({{\alpha}^{2}}-1) \cdot {{\ell}^{2}}\cdot F+96\cdot \Psi\cdot EI \right)}{\displaystyle 2\cdot {{\ell}^{3}}} \cdot \delta\Psi \end{array}</math> | ||
Achtung: hier bezeichnet nun ''α=-1'' den Punkt A, ''α=+1'' den Punkt B. | Achtung: hier bezeichnet nun ''α=-1'' den Punkt A, ''α=+1'' den Punkt B. | ||
| Zeile 134: | Zeile 154: | ||
Diese virtuelle Arbeit des Gesamtsystems spalten wir jetzt nach den [[Sources/Lexikon/virtuelle Verrückung|virtuellen Verrückungen]] auf und erhalten zwei unabhängige Gleichungen in ''V'' und ''ψ'': | Diese virtuelle Arbeit des Gesamtsystems spalten wir jetzt nach den [[Sources/Lexikon/virtuelle Verrückung|virtuellen Verrückungen]] auf und erhalten zwei unabhängige Gleichungen in ''V'' und ''ψ'': | ||
<math>\begin{array}{cc}-\frac{\displaystyle \left( {{\alpha}^{2}}-1\right) \cdot {{\ell}^{3}}\cdot F+64\cdot EI \cdot V}{\displaystyle {{\ell}^{3}}}&=0\\-\frac{\displaystyle 96\cdot \Psi\cdot EI+\left( {{\alpha}^{3}}-\alpha\right) \cdot {{\ell}^{2}}\cdot F}{\displaystyle 2\cdot \ell}&=0\end{array}</math> | ::<math>\begin{array}{cc}-\frac{\displaystyle \left( {{\alpha}^{2}}-1\right) \cdot {{\ell}^{3}}\cdot F+64\cdot EI \cdot V}{\displaystyle {{\ell}^{3}}}&=0\\-\frac{\displaystyle 96\cdot \Psi\cdot EI+\left( {{\alpha}^{3}}-\alpha\right) \cdot {{\ell}^{2}}\cdot F}{\displaystyle 2\cdot \ell}&=0\end{array}</math> | ||
Und die können wir leicht lösen:< | Und die können wir leicht lösen: | ||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
/* Virtual Work of system (equilibrium condition) */ | |||
parts : [/* virtual work of implied external force F*/ | |||
δA = F*δw(x[F]), | |||
/*virt. strain energy*/ | |||
δΠ = integrate(EI*diff(w(x),x,2)*diff(δw(x),x,2),x,-l/2,+l/2)]; | |||
parts : subst([δw(x[F]) = subst([x=\alpha*l/2], subst(forms,δw(x)))],parts); | |||
parts : subst(forms,parts); | |||
PvV : δW = δA-δΠ; | |||
PvV : subst(forms,subst(parts,PvV)); | |||
/* execute differntiation and integration of δW */ | |||
PvV : expand(ev(PvV,nouns)); | |||
/* pick individual equations */ | |||
equs : makelist(coeff(subst(PvV,δW),coords[2][i]),i,1,2); | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
== | <!--------------------------------------------------------------------------------> | ||
{{MyCodeBlock|title=Solve | |||
|text= | |||
In Matrix-Schreibweise stellen wir diesen Ausdruck [[Werkzeuge/Lösungsbausteine der Mathematik/Gewöhnliche lineare Gleichungssysteme|gewöhnliches lineares Gleichungssystem]] dar: | In Matrix-Schreibweise stellen wir diesen Ausdruck [[Werkzeuge/Lösungsbausteine der Mathematik/Gewöhnliche lineare Gleichungssysteme|gewöhnliches lineares Gleichungssystem]] dar: | ||
<math>\underline{\underline{A}}\cdot\underline{x}=\underline{b}</math> | ::<math>\underline{\underline{A}}\cdot\underline{x}=\underline{b}</math> | ||
mit | mit | ||
<math>\underline{\underline{A}}=EI \cdot \begin{pmatrix}-\frac{\displaystyle 64}{\displaystyle {{\ell}^{3}}} & 0\\ 0 & -\frac{\displaystyle 48}{\displaystyle \ell}\end{pmatrix},\underline{b}=F\cdot (\alpha^2-1)\cdot \begin{pmatrix}{1}\\ \frac{\displaystyle \alpha\cdot \ell}{\displaystyle 2}\end{pmatrix}</math> | ::<math>\underline{\underline{A}}=EI \cdot \begin{pmatrix}-\frac{\displaystyle 64}{\displaystyle {{\ell}^{3}}} & 0\\ 0 & -\frac{\displaystyle 48}{\displaystyle \ell}\end{pmatrix},\underline{b}=F\cdot (\alpha^2-1)\cdot \begin{pmatrix}{1}\\ \frac{\displaystyle \alpha\cdot \ell}{\displaystyle 2}\end{pmatrix}</math> | ||
sieht das Gleichungssystem wieder handlich aus, die Lösung ist: | sieht das Gleichungssystem wieder handlich aus, die Lösung ist: | ||
<math>V=-\frac{\displaystyle \left( {{\alpha}^{2}}-1\right) \cdot {{\ell}^{3}}}{\displaystyle 64\cdot EI}\cdot F,\;\;\;\Psi=-\frac{\displaystyle \left( {{\alpha}^{3}}-\alpha\right) \cdot {{\ell}^{2}}}{\displaystyle 96\cdot EI}\cdot F</math> | ::<math>V=-\frac{\displaystyle \left( {{\alpha}^{2}}-1\right) \cdot {{\ell}^{3}}}{\displaystyle 64\cdot EI}\cdot F,\;\;\;\Psi=-\frac{\displaystyle \left( {{\alpha}^{3}}-\alpha\right) \cdot {{\ell}^{2}}}{\displaystyle 96\cdot EI}\cdot F</math> | ||
{{MyAttention|title=Und wissen Sie auch ....|text=... warum A hier eine Diagonalmatrix ist? Schauen Sie sich die Koeffizienten bzgl. von ''α'' an - was erkennen Sie?}} | {{MyAttention|title=Und wissen Sie auch ....|text=... warum A hier eine Diagonalmatrix ist? Schauen Sie sich die Koeffizienten bzgl. von ''α'' an - was erkennen Sie?}} | ||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
1 | /* Mathematical Model */ | ||
ACM : augcoefmatrix(equs,coords[1]); | |||
/* ordinary lineary system of equations*/ | |||
ole : [A = submatrix(ACM,3), b = -col(ACM,3)]; | |||
/* -> here we employ the shortcut via "solve" */ | |||
sol: solve(equs,coords[1])[1]; | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
= | <!--------------------------------------------------------------------------------> | ||
{{MyCodeBlock|title=Post-Process | |||
Die Lösung normieren wir noch für das Post-Processing mit der analytischen maximalen Auslenkung im symmetrischen Belastungsfall (wenn ''F'' in der Mitte zwischen A und B angreift): | |text= | ||
Die Lösung normieren wir noch für das Post-Processing mit dem Fakto ''s'' - der analytischen maximalen Auslenkung im symmetrischen Belastungsfall (wenn ''F'' in der Mitte zwischen A und B angreift): | |||
<math>s = \frac{\displaystyle \ell^3}{\displaystyle 48 EI}\cdot F</math> | ::<math>s = \frac{\displaystyle \ell^3}{\displaystyle 48 EI}\cdot F</math> | ||
Wir tragen sie für verschiedene Kraft-Angriffspunkte (''α=-1,...α=+1'') auf:[[Datei:W8Zt-31.png|mini|Parameterstudie: Auslenkung ''w(a)'' des Kraft-Einleitungspunktes|alternativtext=|ohne]] | Wir tragen sie für verschiedene Kraft-Angriffspunkte (''α=-1,...α=+1'') auf:[[Datei:W8Zt-31.png|mini|Parameterstudie: Auslenkung ''w(a)'' des Kraft-Einleitungspunktes|alternativtext=|ohne]] | ||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
1+1 | /* plot results */ | ||
m : 2; scale : F*l^3/(EI*48); | |||
leg : append([legend],makelist(simplode(["α=",(-m+i)/m]),i,0,2*m)); | |||
plotfct : expand(subst([x=xi*l],subst(sol,subst(forms,w(x)/scale)))); | |||
toplot : makelist(subst([alpha=(-m+i)/m],plotfct),i,0,2*m); | |||
plot2d(subst([alpha=0],toplot),[xi,-1/2,+1/2], [y,-0.05,1.0], leg, | |||
[title, "displacement w for different positions of F"]); | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
| Zeile 197: | Zeile 234: | ||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
1+1 | /* Vergleich mit analytischer Lösung */ | ||
foppl(xi,alpha) := if (xi < alpha) then 0 else xi-alpha; | |||
anplot : F*l^3/(6*EI)*(beta*xi*(1-beta^2-xi^2)+foppl(xi,alpha)^3)/scale; | |||
anplot : subst([beta=1-alpha],anplot); | |||
ritz: subst([xi=xi-1/2],subst(alpha=1/2,expand(subst(sol,makelist(trials[i]*coords[1][i]/scale,i,1,2))))); | |||
plot2d([subst([alpha=3/4],anplot),ritz[1]+ritz[2], ritz[1],ritz[2]],[xi,0,1], | |||
[legend, "analytic", "Ritz", "V-part", "Ψ-part"], | |||
[title, "Vergleich analytische / Ritz - Lösung"]) | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
Aktuelle Version vom 19. April 2021, 10:07 Uhr
Aufgabenstellung
Zu den tabellierten Standardlösungen für den Euler-Bernoulli-Blaken berechnen wir eine Näherungslösung für einen beidseitig gelenkig gelagerten Euler-Bernoulli-Balken:
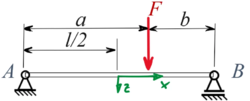
Gesucht ist eine Lösung in Anlehnung an das Verfahren von Ritz - bei dem wir mit Formfunktionen arbeiten, die sich über die gesamte Balkenlänge erstrecken, wir aber im dann mit dem Prinzip der virtuellen Verrückungen arbeiten.
Üblich ist bei Verfahren von Rayleigh-Ritz nämlich sonst das Prinzip vom Minimum der Potentiellen Energie. Die Lösung nach dem Standardverfahren finden Sie hier in W8Zu.
Lösung mit Maxima
Mit dem Föppl-Symbol "<>", sowie
- , und
ist die analytische Lösung:
- .
Bei dieser Lösung hat die unabhängige Koordinate x ihren Ursprung in A - wir verwenden unten einen anderen Ursprung!
Mit den passenden Ansatzfunktionen nach Ritz berechnen Sie eine Näherungslösung des Problems.
Header
Hier arbeiten wir mit Maxima.
/*******************************************************/
/* MAXIMA script */
/* version: wxMaxima 15.08.2 */
/* author: Andreas Baumgart */
/* last updated: 2017-09-14 */
/* ref: TM-C, Labor 3 - aus Gross, Augf. TM 2,Biegestab*/
/* description: finds the approx. solution employing */
/* two polynomial trialfunctions */
/*******************************************************/
Declarations
Wir definieren zunächst die Symbole für die virtuellen Arbeiten und die virtuellen Verrückungen - die in Maxima nicht standardmäßig verfügbar sind.
Die Annahme ℓ>0 brauchen wir, damit Maxima Wurzel-Ausdrücke mit diesem Parameter richtig vereinfachen kann.
/* declare variational variables - see 6.3 Identifiers */
declare("δW", alphabetic);
declare("δA", alphabetic);
declare("δΠ", alphabetic);
declare("δV", alphabetic);
declare("δΨ", alphabetic);
declare("δw", alphabetic);
/* declarations */
assume(l>0);
Formfunctions
Als unabhängige Koordinaten des Balkens wählen wir "x" entlang der Neutralen Faser mit Ursprung in der Mitte zwischen A und B.
Wir entscheiden uns zunächst für zwei abhängige Koordinaten des Systems und deren Variationen (δ)
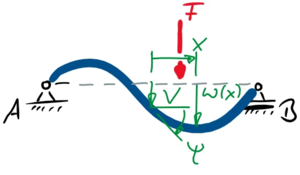
und wählen V und ψ als die Verschiebung und Verdrehung (=Neigung) des Querschnitts im Punkt x=0 des Balkens.
Jetzt brauchen wir zwei Ansatzfunktionen, die unseren Koordinaten V und ψ entsprechen. Wir wollen diese beiden anschaulich denken können - wir wählen einfache Polynome: eine achsensymmetrische und eine punktsymmetrische Funktion mit den noch unbestimmten Konstanten cij:
Diese beiden Funktionen müssen
- Geometrische Randbedingungen erfüllen und
- jeweils mit den Koordinaten V und ψ verknüpft werden.
Die zugehörigen Gleichungen (= die Randbedingungen) sind
- und
mit der Lösung
Anstatt der exakten, bekannten Lösung, verwenden wir in diesem Näherungsansatz also nun die Funktion
- ,
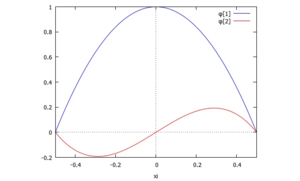
die beiden Koordinaten V und ψ müssen wir noch bestimmen. Die Funktionen, die zu V und ψ gehören, sind rechts aufgetragen:
Klar ist: die exakte Lösung dieses Lastfalls ist eine Funktion, die im Querkraftverlauf am Kraftangriffspunkt (x=a - ℓ/2) einen Sprung hat. Dagegen ist der Querkraftverlauf unserer Näherungslösung stetig differenzierbar und obendrauf noch konstant!
/**** define form functions ***/
/* coordinates */
coords : [[V,Psi], [δV,δΨ]];
/* generic polynomials */
define(v[1](x),sum(c[1,2*i]*x^(2*i),i,0,1));
define(v[2](x),sum(c[2,(2*i+1)]*x^(2*i+1),i,0,1));
/* solve for c's to comply with geometric boundary conditions */
coeffs : append(solve([v[1](0)=V,v[1](+l/2)=0],[c[1,0],c[1,2]])[1],
solve([subst([x=0],diff(v[2](x),x))=Psi,v[2](+l/2)=0],[c[2,1],c[2,3]])[1]);
/* employ in polynomials */
forms : [w(x) = expand(subst(coeffs, sum(v[i](x),i,1,2)))];
forms : append(forms,
[δw(x) = subst(makelist(coords[1][i]=coords[2][i],i,1,2),subst(forms,w(x)))]);
trials: subst([x=l*xi],makelist(coeff(subst(forms,w(x)), coords[1][i]),i,1,2));
plot2d( [trials[1],trials[2]/l],[xi,-1/2,+1/2], [legend, "φ[1]","φ[2]"]);
Equilibrium Conditions
Mit dem Prinzip der virtuellen Verrückungen ist die Gleichgewichtsbedingung immer
Mit den Beiträgen
und dem Einsetzen der Ansatzfunktionen und deren Variation finden wir
Achtung: hier bezeichnet nun α=-1 den Punkt A, α=+1 den Punkt B.
Diese virtuelle Arbeit des Gesamtsystems spalten wir jetzt nach den virtuellen Verrückungen auf und erhalten zwei unabhängige Gleichungen in V und ψ:
Und die können wir leicht lösen:
/* Virtual Work of system (equilibrium condition) */
parts : [/* virtual work of implied external force F*/
δA = F*δw(x[F]),
/*virt. strain energy*/
δΠ = integrate(EI*diff(w(x),x,2)*diff(δw(x),x,2),x,-l/2,+l/2)];
parts : subst([δw(x[F]) = subst([x=\alpha*l/2], subst(forms,δw(x)))],parts);
parts : subst(forms,parts);
PvV : δW = δA-δΠ;
PvV : subst(forms,subst(parts,PvV));
/* execute differntiation and integration of δW */
PvV : expand(ev(PvV,nouns));
/* pick individual equations */
equs : makelist(coeff(subst(PvV,δW),coords[2][i]),i,1,2);
Solve
In Matrix-Schreibweise stellen wir diesen Ausdruck gewöhnliches lineares Gleichungssystem dar:
mit
sieht das Gleichungssystem wieder handlich aus, die Lösung ist:
| ⚠ Und wissen Sie auch ....: |
| ... warum A hier eine Diagonalmatrix ist? Schauen Sie sich die Koeffizienten bzgl. von α an - was erkennen Sie? |
/* Mathematical Model */
ACM : augcoefmatrix(equs,coords[1]);
/* ordinary lineary system of equations*/
ole : [A = submatrix(ACM,3), b = -col(ACM,3)];
/* -> here we employ the shortcut via "solve" */
sol: solve(equs,coords[1])[1];
Post-Process
Die Lösung normieren wir noch für das Post-Processing mit dem Fakto s - der analytischen maximalen Auslenkung im symmetrischen Belastungsfall (wenn F in der Mitte zwischen A und B angreift):
Wir tragen sie für verschiedene Kraft-Angriffspunkte (α=-1,...α=+1) auf:
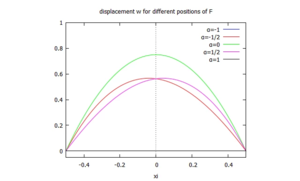
/* plot results */
m : 2; scale : F*l^3/(EI*48);
leg : append([legend],makelist(simplode(["α=",(-m+i)/m]),i,0,2*m));
plotfct : expand(subst([x=xi*l],subst(sol,subst(forms,w(x)/scale))));
toplot : makelist(subst([alpha=(-m+i)/m],plotfct),i,0,2*m);
plot2d(subst([alpha=0],toplot),[xi,-1/2,+1/2], [y,-0.05,1.0], leg,
[title, "displacement w for different positions of F"]);
Post-Process - Vergleich mit analytischer Lösung
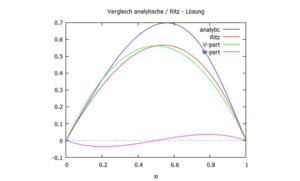
Und wir schauen uns für α=1/2 die Verschiebung der Ritz- und analytischen-Lösung im Vergleich an:
| ✔ Und wissen Sie auch ...: |
| ... wie der Verlauf der Querkraft im Vergleich Ritz / analytisch aussieht? |
/* Vergleich mit analytischer Lösung */
foppl(xi,alpha) := if (xi < alpha) then 0 else xi-alpha;
anplot : F*l^3/(6*EI)*(beta*xi*(1-beta^2-xi^2)+foppl(xi,alpha)^3)/scale;
anplot : subst([beta=1-alpha],anplot);
ritz: subst([xi=xi-1/2],subst(alpha=1/2,expand(subst(sol,makelist(trials[i]*coords[1][i]/scale,i,1,2)))));
plot2d([subst([alpha=3/4],anplot),ritz[1]+ritz[2], ritz[1],ritz[2]],[xi,0,1],
[legend, "analytic", "Ritz", "V-part", "Ψ-part"],
[title, "Vergleich analytische / Ritz - Lösung"])
<Links
- ...
Literature
- ...