Gelöste Aufgaben/UEBK: Unterschied zwischen den Versionen
KKeine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| (Eine dazwischenliegende Version desselben Benutzers wird nicht angezeigt) | |||
| Zeile 8: | Zeile 8: | ||
==Aufgabenstellung== | ==Aufgabenstellung== | ||
Der Euler-Bernoulli-Balken ''AB'' wird durch seine Gewichtskraft belastet. Er ist in ''A'' fest eingespannt und hat eine konstante Breite ''b'' sowie eine zwischen A und B linear veränderliche Höhe ''h''. | |||
Der Lösungsansatz ist für ein Randwertproblem ungewöhnlich: weil das System statisch bestimmt ist, kennen wir alle Zustandsgrößen des Systems am linken Rand sowie deren Differentialbeziehungen und können das Randwertproblem al Anfangswertproblem lösen. | |||
Die analytische Lösung kommt aus [[Gelöste Aufgaben/UEBI|UEBI]]. | |||
<onlyinclude> | <onlyinclude> | ||
[[Datei:UEBF-01.png|200px|left|mini|Lageplan]] | [[Datei:UEBF-01.png|200px|left|mini|Lageplan]] | ||
Gesucht ist | Gesucht ist die Lösung des Problems as Anfangswertproblem - also durch Integration der Differentialbeziehungen. | ||
</onlyinclude> | </onlyinclude> | ||
Gegeben sind für den Balken: | |||
* Länge ''ℓ'', Breite ''b,'' | |||
* E-Modul ''E'', Dichte ''ρ'' und | |||
* die Höhe ''h''<sub>0</sub>''=b'' und ''h<sub>1</sub>'' jeweils in ''A'' und ''B''; dazwischen ist die Höhe linear veränderlich. | |||
== Lösung mit Maxima == | == Lösung mit Maxima == | ||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Header | {{MyCodeBlock|title=Header | ||
|text= | |text= | ||
Auch Randwertprobleme kann man als Anfangswertprobleme lösen. | |||
In diesem Fall sogar besonders einfach. Da das System nämlich statisch bestimmt ist, können wir in ''A'' alle Schnittgrößen und geometrischen Randbedingungen berechnen und dann die Differentialgleichungen für ''Q'', ''M'', ''ϕ'' und ''w'' lösen. | |||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
/*******************************************************/ | |||
/* MAXIMA script */ | |||
/* version: wxMaxima 15.08.2 */ | |||
/* author: Andreas Baumgart */ | |||
/* last updated: 2019-09-01 */ | |||
/* ref: TMC */ | |||
/* description: EBB with I(x), A(x) */ | |||
/* solved as Initial Value Problem */ | |||
/*******************************************************/ | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
<!--------------------------------------------------------------------------------> | <!--------------------------------------------------------------------------------> | ||
{{MyCodeBlock|title=Declarations | {{MyCodeBlock|title=Declarations | ||
|text= | |text= | ||
Die Parameter kopieren wir direkt aus Aufgabe [[Gelöste Aufgaben/UEBI|UEBI]]. | |||
Dazu gehören auch wieder die Referenzgrößen | |||
::<math>\begin{array}{lcl} | |||
\hat{w} &=& \displaystyle \frac{q_{ref} \ell^4}{8\, EI_{ref}}, \\ | |||
\hat{\phi} &=& \displaystyle \frac{w_{ref}}{\ell},\\ | |||
\hat{M} &=& m\, g\, \ell \\ | |||
\hat{Q} &=& m\, g, \\ | |||
q_{ref} &=& \displaystyle \frac{m\, g}{\ell}, \\ | |||
E\, I_{ref}&=& \displaystyle \frac{E\, b \left( \displaystyle \frac{h_0+h_1}{2}\right)^3}{12}] | |||
\end{array}</math>. | |||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
1+1 | /************************************************************/ | ||
/* declare variational variables - see 6.3 Identifiers */ | |||
declare( "ℓ", alphabetic); | |||
declare( "ϕ", alphabetic); | |||
/* system parameters */ | |||
params: [q(xi) = A(xi)*rho*g, | |||
A(xi) = b*h(xi), | |||
I(xi) = b*h(xi)^3/12, | |||
h(xi) = H[0]*(1-xi)+ H[1]*xi]; | |||
params: append(params, | |||
solve((H[0]+H[1])/2*b*ℓ*rho=m, rho)); | |||
geometry : [alpha=1/2]; | |||
dimless: [x = xi*ℓ, H[0]=b, H[1]=alpha*b]; | |||
/* make equations of motion dim'less with load case #1 from Gross e.a., same as UEBI */ | |||
reference : [W[ref] = q[ref]*ℓ^4/8/EI[ref], | |||
ϕ[ref] = q[ref]*ℓ^3/6/EI[ref], | |||
M[ref] = m*g*ℓ, Q[ref] = m*g, | |||
q[ref] = m*g/ℓ, | |||
EI[ref]=E*b*((H[0]+H[1])/2)^3/12]; | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
<!--------------------------------------------------------------------------------> | <!--------------------------------------------------------------------------------> | ||
{{MyCodeBlock|title=Equilibrium Conditions | {{MyCodeBlock|title=Equilibrium Conditions | ||
|text= | |text= | ||
Auch die Differential-Beziehungen nehmen wir aus [[Gelöste Aufgaben/UEBI|UEBI]] zu | |||
::<math>\begin{array}{rrcl} | |||
&Q' &=&-q\\ | |||
&M' &=&+Q\\ | |||
E\,I(x) \; \cdot &\phi' &=& -M\\ | |||
&w' &=&+\phi | |||
\end{array}</math>. | |||
Mit | |||
::<math>\begin{array}{lcl} | |||
Q &=& \hat{Q} \cdot \tilde{Q}\\ | |||
M &=& \hat{M} \cdot \tilde{M}\\ | |||
\phi &=& \hat{\phi} \cdot \tilde{\phi}\\ | |||
w &=& \hat{w} \cdot \tilde{w}\\ | |||
\end{array}</math> | |||
führen wir dimensionslose Koordinaten ein, die die "Zustandsgrößen" unseres Anfangswertproblems sind. Einsetzten liefert dann vier Differentialgleichungen erster Ordnung - der Übersicht halber lassen wir die Tilden hier gleich wieder weg: | |||
::<math>\begin{array}{lcl} | |||
\frac{d}{d\,\xi}\cdot \mathrm{Q}\left( \xi\right) &=&\displaystyle\frac{2\cdot \xi-4}{3}\\ | |||
\frac{d}{d\,\xi}\cdot \mathrm{M}\left( \xi\right) &=&\mathrm{Q}\left( \xi\right) \\ | |||
\frac{d}{d\,\xi}\cdot \mathrm{\phi}\left( \xi\right) &=& \displaystyle\frac{81}{4\xi^3-24\xi^2+48\xi-32} \cdot \mathrm{M}\left( \xi\right) \\ | |||
\frac{d}{d\,\xi}\cdot \mathrm{w}\left( \xi\right) &=&\displaystyle\frac{4}{3} \cdot \mathrm{\phi}\left( \xi\right) | |||
\end{array}</math>, | |||
in symbolischer Schreibweise | |||
::<math>\underline{y}' = \underline{f}(\underline{y}) .</math>. | |||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
1 | /* equations of ""motion */ | ||
dgl : [ Q[ref]*diff(Q(xi),xi)/ℓ = - q(xi), | |||
M[ref]*diff(M(xi),xi)/ℓ = + Q[ref]*Q(xi), | |||
ϕ[ref]*E*I(xi)*diff(ϕ(xi),xi)/ℓ = - M[ref]*M(xi), | |||
W[ref]*diff(w(xi),xi)/ℓ = + ϕ[ref]*ϕ(xi)]; | |||
dgl1stOrder: solve(dgl, [diff(Q(xi),xi), | |||
diff(M(xi),xi), | |||
diff(ϕ(xi),xi), | |||
diff(w(xi),xi)])[1]; | |||
dgl1stOrder: ratsimp(subst(geometry,subst(dimless,subst(params,subst(reference,dgl1stOrder))))); | |||
dgl1stOrder: ratsimp(ev(dgl1stOrder,nouns)); | |||
stateVabs : [Q,M,P,W]; | |||
dgl1stOrder: subst([xi=t],makelist(subst([Q(xi)=Q,M(xi)=M,ϕ(xi)=P,w(xi)=W],rhs(dgl1stOrder[i])),i,1,4)); | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
<!--------------------------------------------------------------------------------> | <!--------------------------------------------------------------------------------> | ||
{{MyCodeBlock|title=Solving | {{MyCodeBlock|title=Solving | ||
|text= | |text= | ||
Das ist ein klassisches Anfangswertproblem, wir brauchen nur noch die Anfangswerte: | |||
::<math>\begin{array}{lcl} | |||
Q(0) &=& m \, g\\ | |||
M(0) &=& \displaystyle \int_0^1 \xi \cdot \rho \, A(\xi)\, g\\ | |||
\phi(0) &=& 0\\ | |||
w(0) &=& 0 | |||
\end{array}</math> | |||
und das dann in dimensionsloser Schreibweise | |||
::<math>\underline{y}(0) = \left( | |||
\begin{array}{c} | |||
1\\ | |||
-\displaystyle \frac{4}{9}\\ | |||
0\\ | |||
0 | |||
\end{array} | |||
\right)</math>. | |||
Das Anfangswertproblem lösen wir mit dem [[Anfangswertprobleme/Methoden zur Lösung von Anfangswertproblemen/Runge-Kutta-Verfahren 4.ter Ordnung|Runge-Kutta-Verfahren 4.ter Ordnung]]. | |||
{{MyTip|title=Schießverfahren|text=Das Lösen ist nicht ganz so einfach, wenn wir nicht alle Anfangsbedingungen kennen. | |||
Trotzdem gibt es dann einen Weg: man wählt erst mal beliebige Anfangsbedingungen und variiert dieses so lange, bis man auf der anderen Seite - hier B - die passenden Randbedingungen Q(1)=0, M(1) = 0 trifft. | |||
Populär ist diese Lösungsmethode für die Einstellung von Artilerie-Geschützen geworden. | |||
Das funktioniert aber auch, wenn man besondere Lösungen sucht - zum Beispiel periodische Lösungen bei Knickformen von Bohrsträngen.}} | |||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
1 | /********************************/ | ||
/* "Anfangs"-Werte */ | |||
y0 : [ Q[0] = 1, | |||
M[0] = -ℓ*integrate(xi*ℓ*A(xi)*rho*g,xi,0,1)/M[ref], | |||
ϕ[0] = 0, | |||
w[0] = 0 | |||
]; | |||
y0 : ratsimp(subst(dimless,subst(params,y0))); | |||
y0 : ev(y0,nouns); | |||
initiVals : makelist(subst(geometry,subst(reference,rhs(y0[i]))),i,1,4); | |||
/********************************/ | |||
/* numerical solution of IVP */ | |||
locations : subst([t0 = 0, tmax = 1, dt = 0.01], | |||
[t, t0, tmax, dt]); | |||
ivs : rk(dgl1stOrder, stateVabs, initiVals, locations)$ | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
<!--------------------------------------------------------------------------------> | <!--------------------------------------------------------------------------------> | ||
{{MyCodeBlock|title=Post-Processing | {{MyCodeBlock|title=Post-Processing | ||
|text= | |text= | ||
[[Datei:UEBK-21.png|mini|Verläufe der "Zustandsgrößen" des Modells ]]Die dimensionslosen Funktionsverläufe tragen wir in einem Diagramm auf - sie passen exakt zur analytischen Lösung in [[Gelöste Aufgaben/UEBI|UEBI]]: | |||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
1 | /********************************/ | ||
/* plot local functions */ | |||
XX : makelist(ivs[j][1],j,1,length(ivs))$ | |||
QQ : makelist(ivs[j][2],j,1,length(ivs))$ | |||
MM : makelist(ivs[j][3],j,1,length(ivs))$ | |||
PP : makelist(ivs[j][4],j,1,length(ivs))$ | |||
WW : makelist(ivs[j][5],j,1,length(ivs))$ | |||
plot2d([[discrete, XX, QQ],[discrete, XX, MM],[discrete, XX, PP],[discrete, XX, WW]], | |||
[gnuplot_preamble, "set yrange [] reverse"], | |||
[xlabel,"x/ℓ->"], [ylabel," <- 1"], | |||
[legend, "Q/Q_ref", "M/M_ref", "ϕ/ϕ_ref", "w/w_ref"]); | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
<hr/> | <hr /> | ||
'''Links''' | '''Links''' | ||
* | * [[Gelöste Aufgaben/UEBI|UEBI]] | ||
'''Literature''' | '''Literature''' | ||
* ... | * ... | ||
Aktuelle Version vom 17. April 2021, 07:37 Uhr
Aufgabenstellung
Der Euler-Bernoulli-Balken AB wird durch seine Gewichtskraft belastet. Er ist in A fest eingespannt und hat eine konstante Breite b sowie eine zwischen A und B linear veränderliche Höhe h.
Der Lösungsansatz ist für ein Randwertproblem ungewöhnlich: weil das System statisch bestimmt ist, kennen wir alle Zustandsgrößen des Systems am linken Rand sowie deren Differentialbeziehungen und können das Randwertproblem al Anfangswertproblem lösen.
Die analytische Lösung kommt aus UEBI.
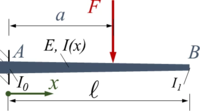
Gesucht ist die Lösung des Problems as Anfangswertproblem - also durch Integration der Differentialbeziehungen.
Gegeben sind für den Balken:
- Länge ℓ, Breite b,
- E-Modul E, Dichte ρ und
- die Höhe h0=b und h1 jeweils in A und B; dazwischen ist die Höhe linear veränderlich.
Lösung mit Maxima
Header
Auch Randwertprobleme kann man als Anfangswertprobleme lösen.
In diesem Fall sogar besonders einfach. Da das System nämlich statisch bestimmt ist, können wir in A alle Schnittgrößen und geometrischen Randbedingungen berechnen und dann die Differentialgleichungen für Q, M, ϕ und w lösen.
/*******************************************************/
/* MAXIMA script */
/* version: wxMaxima 15.08.2 */
/* author: Andreas Baumgart */
/* last updated: 2019-09-01 */
/* ref: TMC */
/* description: EBB with I(x), A(x) */
/* solved as Initial Value Problem */
/*******************************************************/
Declarations
Die Parameter kopieren wir direkt aus Aufgabe UEBI.
Dazu gehören auch wieder die Referenzgrößen
- .
/************************************************************/
/* declare variational variables - see 6.3 Identifiers */
declare( "ℓ", alphabetic);
declare( "ϕ", alphabetic);
/* system parameters */
params: [q(xi) = A(xi)*rho*g,
A(xi) = b*h(xi),
I(xi) = b*h(xi)^3/12,
h(xi) = H[0]*(1-xi)+ H[1]*xi];
params: append(params,
solve((H[0]+H[1])/2*b*ℓ*rho=m, rho));
geometry : [alpha=1/2];
dimless: [x = xi*ℓ, H[0]=b, H[1]=alpha*b];
/* make equations of motion dim'less with load case #1 from Gross e.a., same as UEBI */
reference : [W[ref] = q[ref]*ℓ^4/8/EI[ref],
ϕ[ref] = q[ref]*ℓ^3/6/EI[ref],
M[ref] = m*g*ℓ, Q[ref] = m*g,
q[ref] = m*g/ℓ,
EI[ref]=E*b*((H[0]+H[1])/2)^3/12];
Equilibrium Conditions
Auch die Differential-Beziehungen nehmen wir aus UEBI zu
- .
Mit
führen wir dimensionslose Koordinaten ein, die die "Zustandsgrößen" unseres Anfangswertproblems sind. Einsetzten liefert dann vier Differentialgleichungen erster Ordnung - der Übersicht halber lassen wir die Tilden hier gleich wieder weg:
- ,
in symbolischer Schreibweise
- .
/* equations of ""motion */
dgl : [ Q[ref]*diff(Q(xi),xi)/ℓ = - q(xi),
M[ref]*diff(M(xi),xi)/ℓ = + Q[ref]*Q(xi),
ϕ[ref]*E*I(xi)*diff(ϕ(xi),xi)/ℓ = - M[ref]*M(xi),
W[ref]*diff(w(xi),xi)/ℓ = + ϕ[ref]*ϕ(xi)];
dgl1stOrder: solve(dgl, [diff(Q(xi),xi),
diff(M(xi),xi),
diff(ϕ(xi),xi),
diff(w(xi),xi)])[1];
dgl1stOrder: ratsimp(subst(geometry,subst(dimless,subst(params,subst(reference,dgl1stOrder)))));
dgl1stOrder: ratsimp(ev(dgl1stOrder,nouns));
stateVabs : [Q,M,P,W];
dgl1stOrder: subst([xi=t],makelist(subst([Q(xi)=Q,M(xi)=M,ϕ(xi)=P,w(xi)=W],rhs(dgl1stOrder[i])),i,1,4));
Solving
Das ist ein klassisches Anfangswertproblem, wir brauchen nur noch die Anfangswerte:
und das dann in dimensionsloser Schreibweise
- .
Das Anfangswertproblem lösen wir mit dem Runge-Kutta-Verfahren 4.ter Ordnung.
| ✔ Schießverfahren: |
| Das Lösen ist nicht ganz so einfach, wenn wir nicht alle Anfangsbedingungen kennen.
Trotzdem gibt es dann einen Weg: man wählt erst mal beliebige Anfangsbedingungen und variiert dieses so lange, bis man auf der anderen Seite - hier B - die passenden Randbedingungen Q(1)=0, M(1) = 0 trifft. Populär ist diese Lösungsmethode für die Einstellung von Artilerie-Geschützen geworden. Das funktioniert aber auch, wenn man besondere Lösungen sucht - zum Beispiel periodische Lösungen bei Knickformen von Bohrsträngen. |
/********************************/
/* "Anfangs"-Werte */
y0 : [ Q[0] = 1,
M[0] = -ℓ*integrate(xi*ℓ*A(xi)*rho*g,xi,0,1)/M[ref],
ϕ[0] = 0,
w[0] = 0
];
y0 : ratsimp(subst(dimless,subst(params,y0)));
y0 : ev(y0,nouns);
initiVals : makelist(subst(geometry,subst(reference,rhs(y0[i]))),i,1,4);
/********************************/
/* numerical solution of IVP */
locations : subst([t0 = 0, tmax = 1, dt = 0.01],
[t, t0, tmax, dt]);
ivs : rk(dgl1stOrder, stateVabs, initiVals, locations)$
Post-Processing
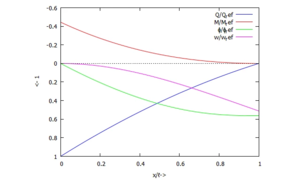
Die dimensionslosen Funktionsverläufe tragen wir in einem Diagramm auf - sie passen exakt zur analytischen Lösung in UEBI:
/********************************/
/* plot local functions */
XX : makelist(ivs[j][1],j,1,length(ivs))$
QQ : makelist(ivs[j][2],j,1,length(ivs))$
MM : makelist(ivs[j][3],j,1,length(ivs))$
PP : makelist(ivs[j][4],j,1,length(ivs))$
WW : makelist(ivs[j][5],j,1,length(ivs))$
plot2d([[discrete, XX, QQ],[discrete, XX, MM],[discrete, XX, PP],[discrete, XX, WW]],
[gnuplot_preamble, "set yrange [] reverse"],
[xlabel,"x/ℓ->"], [ylabel," <- 1"],
[legend, "Q/Q_ref", "M/M_ref", "ϕ/ϕ_ref", "w/w_ref"]);
Links
Literature
- ...