Sources/Lexikon/Euler-Bernoulli-Balken/Standard-Lösungen: Unterschied zwischen den Versionen
Zur Navigation springen
Zur Suche springen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| (7 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 14: | Zeile 14: | ||
==Balken unter Endmoment== | ==Balken unter Endmoment== | ||
<table class="wikitable" style="background-color:white;"> | |||
<tr><th>Skizze</th><th><math>E\,I\,w'_A</math></th><th><math>E\,I\,w'_B</math></th><th><math>E\,I\,w(\xi)</math></th><th><math>E\,I\,w_{max}</math></th></tr> | |||
<tr><td>[[Datei:EBB-load-case-02.png|alternativtext=|rahmenlos|200x200px]]</td><td><math>0</math></td><td><math>M\,\ell</math></td><td><math>\displaystyle \frac{1}{2} M\, \ell^2 \, \xi^2</math></td><td><math>\displaystyle \frac{1}{2} M\, \ell^2</math></td></tr> | |||
</table> | |||
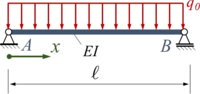
==Balken Streckenlast== | ==Balken Streckenlast== | ||
<table class="wikitable" style="background-color:white;"> | |||
<tr><th>Skizze</th><th><math>E\,I\,w'_A</math></th><th><math>E\,I\,w'_B</math></th><th><math>E\,I\,w(\xi)</math></th><th><math>E\,I\,w_{max}</math></th></tr> | |||
<tr><td>[[Datei:EBB-load-case-03.png|alternativtext=|rahmenlos|200x200px]]</td><td><math>\displaystyle \frac{q_0\; \ell^3}{24}</math></td><td><math>\displaystyle -\frac{q_0\; \ell^3}{24}</math></td><td><math>\displaystyle \frac{q_0\; \ell^4}{24}\left(3 \xi^5 - 10 \xi^3 + 7 \xi \right)</math></td><td><math>\displaystyle \frac{5\, q_0\; \ell^4}{384}</math></td></tr> | |||
</table> | |||
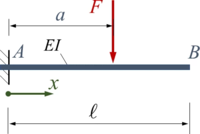
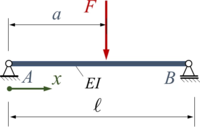
==Einzellast, doppeltgelenkige Lagerung== | ==Einzellast, doppeltgelenkige Lagerung== | ||
<table class="wikitable" style="background-color:white;"> | |||
<tr><th>Skizze</th><th><math>E\,I\,w'_A</math></th><th><math>E\,I\,w'_B</math></th><th><math>E\,I\,w(\xi)</math></th><th><math>E\,I\,w_{max}</math></th></tr> | |||
<tr><td>[[Datei:EBB-load-case-04.png|alternativtext=|rahmenlos|200x200px]]</td><td><math>\displaystyle \frac{F\; \ell^2}{6} \left({{\alpha}^{3}}-3\cdot {{\alpha}^{2}}+2\cdot \alpha\right)</math></td><td><math>\displaystyle -\frac{F\; \ell^2}{6} \left({{-\alpha}^{3}}+ \alpha\right)</math></td><td><math>\displaystyle \frac{F\; \ell^3}{6} \left(\left( \alpha-1\right) \cdot {{\xi}^{4}}+\left( 2\cdot \alpha-3\cdot {{\alpha}^{2}}+{{\alpha}^{3}}\right) \cdot \xi + <\xi-\alpha>^3\right)</math></td><td><math>\displaystyle \frac{F\; \ell^3}{48} \text{ für } \alpha = 1/2</math></td></tr> | |||
</table> | |||
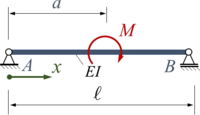
==Einzelmoment, doppeltgelenkige Lagerung== | ==Einzelmoment, doppeltgelenkige Lagerung== | ||
<table class="wikitable" style="background-color:white;"> | |||
<tr><th>Skizze</th><th><math>E\,I\,w'_A</math></th><th><math>E\,I\,w'_B</math></th><th><math>E\,I\,w(\xi)</math></th><th><math>E\,I\,w_{max}</math></th></tr> | |||
<tr><td>[[Datei:EBB-load-case-05.png|alternativtext=|rahmenlos|200x200px]]</td><td><math>\begin{array}{ll}&\displaystyle \frac{M\; \ell}{6} \left( 3\cdot {{\alpha}^{2}}-6\cdot \alpha+2 \right)\\=& \displaystyle -\frac{M\; \ell}{24} \text{ für }\alpha=1/2, \xi= 0\end{array}</math></td><td><math>\displaystyle \frac{M\; \ell}{6} \left(3\,\alpha^2-1\right)</math></td><td><math>\displaystyle \frac{M\; \ell^2}{6} \left( | |||
\xi^3+\xi (2-6 \alpha+3 \alpha^2) - 3\cdot <\xi-\alpha>^2\right)</math></td><td><math>\displaystyle \frac{M\; \ell^2}{72\;\sqrt{3}} \text{ für } \alpha = 1/2</math>{{MyAttention|title=Achtung|text=! Das ist das Maximum der Auslenkung für α=1/2, | |||
nicht das absolute Maximum !}}</td></tr></table> | |||
{{MyCodeBlock| | |||
title=Maxima Source Code | |||
|text=Zum Nachrechnen steht hier der Quellcodes des CAS. | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
/*******************************************************/ | |||
/* MAXIMA script */ | |||
/* version: wxMaxima 15.08.2 */ | |||
/* author: Andreas Baumgart */ | |||
/* last updated: 2018-02-16 */ | |||
/* ref: TMC, Labor 3 */ | |||
/* description: analytische Lösung für load-case-5 */ | |||
/* */ | |||
/*******************************************************/ | |||
feld: makelist(w[i](x) = sum(C[i,j]*x^j,j,0,3),i,1,2); | |||
BC : [subst([x=0], subst(feld,w[1](x)) )=0, | |||
subst([x=0],diff(subst(feld,w[1](x)),x,2))=0, | |||
subst([x=a], subst(feld,w[1](x)) )=subst([x=a], subst(feld,w[2](x)) ), | |||
subst([x=a],diff(subst(feld,w[1](x)),x,1))=subst([x=a],diff(subst(feld,w[2](x)),x,1)), | |||
subst([x=a],diff(subst(feld,w[1](x)),x,3))=subst([x=a],diff(subst(feld,w[2](x)),x,3)), | |||
EI*subst([x=a],diff(subst(feld,w[1](x)),x,2))-M=EI*subst([x=a],diff(subst(feld,w[2](x)),x,2)), | |||
subst([x=l], subst(feld,w[2](x)) )=0, | |||
subst([x=l],diff(subst(feld,w[2](x)),x,2))=0]; | |||
IC : flatten(makelist(makelist(C[i,j],j,0,3),i,1,2)); | |||
sol[1]: solve(BC,IC)[1]; | |||
sol[2]: ratsimp(subst([x=xi*l,a=alpha*l],subst(sol[1],feld))); | |||
/* foeppel - part */ | |||
expand(subst(sol[2],w[2](xi*l)-w[1](xi*l))/(M*l^2/(6*EI))); | |||
ratsimp(subst(sol[2],w[1](xi*l))/(M*l^2/(6*EI))); | |||
plot2d(subst([xi=t,alpha=1/2],[[parametric,xi,subst(sol[2],w[1](xi*l))/(M*l^2/(6*EI)),[t,0,alpha]], | |||
[parametric,xi,subst(sol[2],w[2](xi*l))/(M*l^2/(6*EI)),[t,alpha,1]]]), | |||
[legend,"ξ<α","ξ>α"], | |||
[xlabel, "x/l →"], | |||
[ylabel, "w(x)/W →"]); | |||
/* maximum */ | |||
maxi : solve(diff(subst([alpha=1/2],subst(sol[2],w[1](xi*l))),xi)=0,xi); | |||
WM : -subst([3^(5/2) = 3^2*sqrt(3)], ratsimp(subst(maxi[2],subst([alpha=1/2],subst(sol[2],w[1](xi*l)))))); | |||
PM : ratsimp(subst([xi=0],subst([alpha=1/2],diff(subst(sol[2],w[1](xi*l)),xi)/l))); | |||
</syntaxhighlight>}} | |||
==Kragbalken Streckenlast== | ==Kragbalken Streckenlast== | ||
<table class="wikitable" style="background-color:white;"> | |||
<tr><th>Skizze</th><th><math>E\,I\,w'_A</math></th><th><math>E\,I\,w'_B</math></th><th><math>E\,I\,w(\xi)</math></th><th><math>E\,I\,w_{max}</math></th></tr> | |||
<tr><td>[[Datei:EBB-load-case-06.png|alternativtext=|rahmenlos|200x200px]]</td><td><math>0</math></td><td><math>\displaystyle \frac{q_0\; \ell^3}{6}</math></td><td><math>\displaystyle \frac{q_0\; \ell^4}{24}\left(\xi^4 - 4 \xi^3 + 6 \xi^2 \right)</math></td><td><math>\displaystyle \frac{q_0\; \ell^4}{8}</math></td></tr> | |||
</table> | |||
Aktuelle Version vom 16. April 2021, 10:10 Uhr
Biegelinien-Tabelle in Anlehnung an Literatur: Gross e.a.: Formeln und Aufgaben zur Technischen Mechanik 2.
Wir nutzen dafür
Das Föppel-Symbol:
Eine Dimensionslose Schreibweise:
,
Kragbalken
| Skizze | ||||
|---|---|---|---|---|
 |
Balken unter Endmoment
| Skizze | ||||
|---|---|---|---|---|
 |
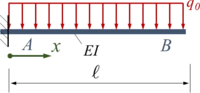
Balken Streckenlast
| Skizze | ||||
|---|---|---|---|---|
 |
Einzellast, doppeltgelenkige Lagerung
| Skizze | ||||
|---|---|---|---|---|
 |
Einzelmoment, doppeltgelenkige Lagerung
| Skizze | ||||||
|---|---|---|---|---|---|---|
 |
|
Maxima Source Code
Zum Nachrechnen steht hier der Quellcodes des CAS.
/*******************************************************/
/* MAXIMA script */
/* version: wxMaxima 15.08.2 */
/* author: Andreas Baumgart */
/* last updated: 2018-02-16 */
/* ref: TMC, Labor 3 */
/* description: analytische Lösung für load-case-5 */
/* */
/*******************************************************/
feld: makelist(w[i](x) = sum(C[i,j]*x^j,j,0,3),i,1,2);
BC : [subst([x=0], subst(feld,w[1](x)) )=0,
subst([x=0],diff(subst(feld,w[1](x)),x,2))=0,
subst([x=a], subst(feld,w[1](x)) )=subst([x=a], subst(feld,w[2](x)) ),
subst([x=a],diff(subst(feld,w[1](x)),x,1))=subst([x=a],diff(subst(feld,w[2](x)),x,1)),
subst([x=a],diff(subst(feld,w[1](x)),x,3))=subst([x=a],diff(subst(feld,w[2](x)),x,3)),
EI*subst([x=a],diff(subst(feld,w[1](x)),x,2))-M=EI*subst([x=a],diff(subst(feld,w[2](x)),x,2)),
subst([x=l], subst(feld,w[2](x)) )=0,
subst([x=l],diff(subst(feld,w[2](x)),x,2))=0];
IC : flatten(makelist(makelist(C[i,j],j,0,3),i,1,2));
sol[1]: solve(BC,IC)[1];
sol[2]: ratsimp(subst([x=xi*l,a=alpha*l],subst(sol[1],feld)));
/* foeppel - part */
expand(subst(sol[2],w[2](xi*l)-w[1](xi*l))/(M*l^2/(6*EI)));
ratsimp(subst(sol[2],w[1](xi*l))/(M*l^2/(6*EI)));
plot2d(subst([xi=t,alpha=1/2],[[parametric,xi,subst(sol[2],w[1](xi*l))/(M*l^2/(6*EI)),[t,0,alpha]],
[parametric,xi,subst(sol[2],w[2](xi*l))/(M*l^2/(6*EI)),[t,alpha,1]]]),
[legend,"ξ<α","ξ>α"],
[xlabel, "x/l →"],
[ylabel, "w(x)/W →"]);
/* maximum */
maxi : solve(diff(subst([alpha=1/2],subst(sol[2],w[1](xi*l))),xi)=0,xi);
WM : -subst([3^(5/2) = 3^2*sqrt(3)], ratsimp(subst(maxi[2],subst([alpha=1/2],subst(sol[2],w[1](xi*l))))));
PM : ratsimp(subst([xi=0],subst([alpha=1/2],diff(subst(sol[2],w[1](xi*l)),xi)/l)));
Kragbalken Streckenlast
| Skizze | ||||
|---|---|---|---|---|
 |