Gelöste Aufgaben/UEBB: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| (3 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
[[Category:Gelöste Aufgaben]] | |||
[[ | [[Category:Dimensionslose Schreibweise]] | ||
[[Category:A*x=b]] | |||
[[Category:Numerische Lösung]] | |||
[[Category:Randwertproblem]] | |||
[[Category:Potential]] | |||
[[Category:Prinzip vom Minimum der Potentiellen Energie]] | |||
[[Category:Biege-Belastung]] | |||
[[Category:Euler-Bernoulli-Balken]] | |||
[[Category:Rayleigh-Ritz-Prinzip]] | |||
[[Category:Matlab]] | |||
==Aufgabenstellung== | |||
<onlyinclude> | |||
[[Datei:UEBB-01.png|250x250px|left|mini|Lageplan|alternativtext=]] | |||
Der [[Sources/Lexikon/Euler-Bernoulli-Balken|Euler-Bernoulli-Balken]] AB wird durch eine linear veränderliche Streckenlast belastet. | |||
Gesucht ist die Lösung für ''w(x)'' mit dem Ansatz von Ritz und zwei Trial-Functions. | |||
</onlyinclude> | |||
== Lösung mit Matlab == | |||
Für dieses Problem finden wir in der Literatur die tabellierte Musterlösung | |||
[[Datei:UEBB- | ::<math>EI\cdot w(x) = \displaystyle \frac{q_A \ell^4}{120} \left(-1\cdot\xi^5 + 5\cdot\xi^4 - 10\cdot\xi^3 + 10\cdot\xi^2\right)</math>. | ||
[[Datei:UEBB-21.png|mini|Vergleich von analytischer und genäherter Lösung]] | |||
Die verwenden wir als Referenz, um die Qualität unserer Näherungslösung zu bewerten. Die Auslenkung der analytischen Lösung ist am rechten Rand (''x=ℓ'') ist maximal und beträgt | |||
::<math>\displaystyle w(\ell) = \frac{q_A\;\ell^4}{30\; EI} =: \hat{w}</math>Damit können wir die beiden Lösungen vergleichen und die Bewegungsgleichung nach Ritz dimensionslos machen. | |||
Für den Ritz-Ansatz brauchen wir die Terme der Potentiellen Energie des Systems | |||
::<math>U = \Pi -A</math>, | |||
wobei '''''Π''''' die Formänderungsenergie ist und '''''A''''' die Arbeitsfunktion der äußeren Last ''q(x)''. | |||
Es ist | |||
::<math>\begin{array}{ll} \Pi & = \displaystyle \frac{1}{2} \int_\ell EI\;(w'')^2 dx \\ \displaystyle A & = \displaystyle \int_\ell q(x)\cdot w(x) dx \text{ mit } q(x) = q_A \left(1-\frac{x}{\ell}\right)\end{array}</math>Für den Ritz-Ansatz verwenden wir Ganzfeld-Ansätze - also Formfunktionen für die Näherung der exakten Lösung, die sich über die gesamte Balkenlänge erstrecken. | |||
Der Ansatz ist allgemein | |||
::<math>\tilde{w}(x) = \sum W_i\cdot \phi_i(x)</math>, | |||
wobei die ''ϕ<sub>i</sub>'' die linear unabhängigen Formfunktionen und die ''W<sub>i</sub>'' die Wichtungsfaktoren sind, die wir so bestimmen, dass die Gesamtlösung bestmöglich die gesuchte Funktion approximiert. | |||
Für die wählen wir ausschließlich Polynome - die können wir bequem differenzieren und integrieren. | |||
{{MyTip|title=Matlab© und Polynome|text=Alle verwendeten Funktionen in diesem Beispiel sind Polynome. Matlab© bietet für die Manipulation von Polynomen eine Klasse von Functions an, die hier hilfreich sind: | |||
* [https://de.mathworks.com/help/matlab/polynomials.html Matlab©: Polynomials] | |||
}} | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Header | |||
|text=Lösung mit Matlab R2015a | |||
|code= | |||
<syntaxhighlight lang="Matlab" line start=1> | |||
%*****************************************************% | |||
% Matlab script % | |||
% version: Matlab R2015a % | |||
% author: Andreas Baumgart % | |||
% last updated: 2017-10-19 % | |||
% ref: Gross e.a. TM 2 - Aufgaben zu Biegung, #7 % | |||
% description: Lösung mit Ritz-Ansatz % | |||
% % | |||
%*****************************************************% | |||
</syntaxhighlight> | |||
}} | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Formfunctions | |||
|text= | |||
Wir setzen zuerst für die Näherungslösung | |||
::<math>\displaystyle \tilde{w}(x) = \tilde{W}_2\cdot \underbrace{\left(\frac{x}{\ell}\right)^2}_{\displaystyle =: \phi_2} + \tilde{W}_3\cdot \underbrace{\left(\frac{x}{\ell}\right)^3}_{\displaystyle =: \phi_3}</math> | |||
an - in der die beiden ''ϕ<sub>i</sub>'' die geometrischen Randbedingungen | |||
::<math>\begin{array}{ll}\phi_i(0) &= 0\\\displaystyle \frac{d \phi_i}{dx}|_{x=0}& = 0 \end{array}</math> | |||
erfüllen. | |||
Wir setzen jetzt dimensionslos an, also | |||
::<math>\tilde{W}_i = \ell_{Bez}\cdot W_i</math> | |||
und wählen als Bezugslänge | |||
::<math>\ell_{Bez} := \displaystyle \hat{w} = \frac{q_A\;\ell^4}{30\; EI}</math> | |||
Die berechnete Auslenkung des Balkens am rechten Rand sollte also im Idealfall - wenn analytische und approximierte Lösung gleich sind - zusammenfallen. Dann müssten wir herausbekommen: | |||
::<math>W_2 + W_3 = 1</math> | |||
Zusätzlich schreiben die ''ϕ<sub>i</sub>'' mit der dimensionslose Koordinate ''ξ'', so dass | |||
::<math>\phi_2 = \xi^2 \text{ und } \phi_3 = \xi^3</math> | |||
In Matlab-Notation sind das die Polynome<blockquote><blockquote><code>[0,1,0,0]</code> und <code>[1,0,0,0]</code>.</blockquote></blockquote>Uns fehlt noch das Polynom für die Streckenlast | |||
::<math>q(x) = q_A\left(1 - \displaystyle \frac{x}{\ell}\right)</math>, | |||
in Matlab bilden wir es durch <code>[-1,1]</code> ab. | |||
|code= | |||
<syntaxhighlight lang="Matlab" line start=1> | |||
% Ansatz-Polynome Definieren | |||
% diese erfüllen die geometrischen Randbedingungen | |||
phi = [[0,1,0,0];[1,0,0,0]] | |||
% Matrizen für das lineare Gleichungssystem | |||
% in W[2] und W[3] vorbereiten | |||
A = zeros(2,2) | |||
b = zeros(2,1) | |||
</syntaxhighlight> | |||
}} | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Potential Energy | |||
|text=Für die Gleichgewichtsbedingungen setzten wir ''Π'' und ''A'' in ''U'' ein und schreiben die skalare Gleichung in Matrizenform an. Dabei müssen wir | |||
::<math>\displaystyle \frac{d\phi}{x} = \frac{d\phi}{\xi}\cdot\underbrace{\displaystyle\frac{d\xi}{x}}_{\displaystyle = \frac{1}{\ell}}</math> | |||
und erhalten | |||
::<math>U = \frac{1}{2} EI \displaystyle \frac{\hat{w}^2}{\ell^3}\underline{W}^T \cdot \underline{\underline{A}}\cdot \underline{W} - q_A \; \ell\; \hat{w}\;\underline{W}^T\cdot \underline{b} </math> | |||
mit | |||
::<math>a_{i,j} = \displaystyle\int_0^1 \phi_i''(\xi) \cdot \phi_j''(\xi) d\xi \text{ und } b_i = \int_0^1 \left(1-\xi\right) \cdot \phi_i(\xi) d\xi</math>. | |||
Mit der analytischen Lösung für ''w(ℓ)'' oben bleibt | |||
::<math>\displaystyle U = \hat{w}\; q_A\; \ell \left( \displaystyle \frac{1}{2}\;\frac{1}{30}\,\underline{W}^T \cdot \underline{\underline{A}}\cdot \underline{W} - \underline{W}^T\cdot \underline{b} \right)</math> | |||
mit | |||
::<math>\underline{\underline{A}} = \left(\begin{array}{c}4&6\\6&12 \end{array}\right), \underline{b} = \displaystyle \frac{1}{60}\cdot \left(\begin{array}{c}5\\3 \end{array}\right)</math>. | |||
Die seltsam anmutende Notation mit 1/2*1/30 hat seinen Sinn in der Anknüpfung an die [[Sources/Lexikon/Minimum Prinzipe|Minimum Prinzipe]] und die Lösung der Gleichgewichtsbeziehungen. | |||
|code= | |||
<syntaxhighlight lang="Matlab" line start=1> | |||
% Matrizen besetzen | |||
for i= 1:2 | |||
for j=1:2 | |||
E = conv( | |||
polyder(polyder(phi(i,:))), | |||
polyder(polyder(phi(j,:)))) | |||
I = polyint(E) | |||
A(i,j) = diff(polyval(I,[0 1])) | |||
end | |||
b(i,1) = diff(polyval(polyint( | |||
conv([-1,1],phi(i,:))), | |||
[0 1])) | |||
end | |||
</syntaxhighlight> | |||
}} | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Equilibrium Conditions | |||
|text= | |||
Diese Gleichung erfüllt die Gleichgewichtsbedingungen | |||
::<math>\displaystyle \frac{dU}{dW_i} \stackrel{!}{=} 0</math>, | |||
wenn | |||
::<math>\frac{1}{30}\underline{\underline{A}}\; \underline{W} = \underline{b}</math>. | |||
|code= | |||
<syntaxhighlight lang="Matlab" line start=1> | |||
% left blank intentionally | |||
</syntaxhighlight> | |||
}} | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Solving | |||
|text= | |||
Das lineare Gleichungssystem löst in Matlab der Befehl | |||
::<code>linsolve(.,.)</code> für uns. | |||
[[Datei:UEBB-11.png|mini|Matlab: linsolve!|alternativtext=|ohne|200x200px]] | |||
Hier ist | |||
::<math>\underline{x} = \left[ \begin{array}{c}W_2\\W_3\end{array}\right]</math> | |||
und wir sehen: unser Wunsch | |||
::<math>W_2+W_3 = 1</math> | |||
von oben ist sogar exakt - nicht nur näherungsweise - erfüllt! | |||
|code= | |||
<syntaxhighlight lang="Matlab" line start=1> | |||
% nach x (W[2],W[3]) lösen | |||
x = linsolve(A/30,b) | |||
</syntaxhighlight> | |||
}} | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Post-Processing | |||
|text= | |||
Die Näherungslösung und die analytische Lösung können wir jetzt im Vergleich auftragen: | |||
[[Datei:UEBB-21.png|mini|Vergleich von analytischer und genäherter Lösung|alternativtext=|ohne]] | |||
|code= | |||
<syntaxhighlight lang="Matlab" line start=1> | |||
% … und plotten | |||
% analytische Ösung | |||
a = [-1,5,-10,+10,0,0]/4. | |||
% genäherte Lösung in Teilen | |||
w = [x(1)*phi(1,:); | |||
x(2)*phi(2,:)] | |||
xi = linspace(0,1,100) | |||
p = [polyval(a,xi); | |||
polyval(w(1,:),xi); | |||
polyval(w(2,:),xi)] | |||
fig = plot(xi,p(1,:),xi,p(2,:)+p(3,:)) | |||
title('analytische und approximierte Lösung') | |||
xlabel('ξ →') | |||
ylabel('w →') | |||
legend('analytic','Ritz-approx.') | |||
</syntaxhighlight> | |||
}} | |||
<hr/> | |||
'''Links''' | |||
* ... | |||
'''Literature''' | |||
* ... | |||
Aktuelle Version vom 13. April 2021, 08:59 Uhr
Aufgabenstellung
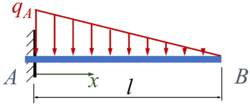
Der Euler-Bernoulli-Balken AB wird durch eine linear veränderliche Streckenlast belastet. Gesucht ist die Lösung für w(x) mit dem Ansatz von Ritz und zwei Trial-Functions.
Lösung mit Matlab
Für dieses Problem finden wir in der Literatur die tabellierte Musterlösung
- .
Die verwenden wir als Referenz, um die Qualität unserer Näherungslösung zu bewerten. Die Auslenkung der analytischen Lösung ist am rechten Rand (x=ℓ) ist maximal und beträgt
- Damit können wir die beiden Lösungen vergleichen und die Bewegungsgleichung nach Ritz dimensionslos machen.
Für den Ritz-Ansatz brauchen wir die Terme der Potentiellen Energie des Systems
- ,
wobei Π die Formänderungsenergie ist und A die Arbeitsfunktion der äußeren Last q(x).
Es ist
- Für den Ritz-Ansatz verwenden wir Ganzfeld-Ansätze - also Formfunktionen für die Näherung der exakten Lösung, die sich über die gesamte Balkenlänge erstrecken.
Der Ansatz ist allgemein
- ,
wobei die ϕi die linear unabhängigen Formfunktionen und die Wi die Wichtungsfaktoren sind, die wir so bestimmen, dass die Gesamtlösung bestmöglich die gesuchte Funktion approximiert.
Für die wählen wir ausschließlich Polynome - die können wir bequem differenzieren und integrieren.
| ✔ Matlab© und Polynome: |
| Alle verwendeten Funktionen in diesem Beispiel sind Polynome. Matlab© bietet für die Manipulation von Polynomen eine Klasse von Functions an, die hier hilfreich sind: |
Header
Lösung mit Matlab R2015a
%*****************************************************%
% Matlab script %
% version: Matlab R2015a %
% author: Andreas Baumgart %
% last updated: 2017-10-19 %
% ref: Gross e.a. TM 2 - Aufgaben zu Biegung, #7 %
% description: Lösung mit Ritz-Ansatz %
% %
%*****************************************************%
Formfunctions
Wir setzen zuerst für die Näherungslösung
an - in der die beiden ϕi die geometrischen Randbedingungen
erfüllen.
Wir setzen jetzt dimensionslos an, also
und wählen als Bezugslänge
Die berechnete Auslenkung des Balkens am rechten Rand sollte also im Idealfall - wenn analytische und approximierte Lösung gleich sind - zusammenfallen. Dann müssten wir herausbekommen:
Zusätzlich schreiben die ϕi mit der dimensionslose Koordinate ξ, so dass
In Matlab-Notation sind das die Polynome
[0,1,0,0]und[1,0,0,0].
Uns fehlt noch das Polynom für die Streckenlast
- ,
in Matlab bilden wir es durch [-1,1] ab.
% Ansatz-Polynome Definieren
% diese erfüllen die geometrischen Randbedingungen
phi = [[0,1,0,0];[1,0,0,0]]
% Matrizen für das lineare Gleichungssystem
% in W[2] und W[3] vorbereiten
A = zeros(2,2)
b = zeros(2,1)
Potential Energy
Für die Gleichgewichtsbedingungen setzten wir Π und A in U ein und schreiben die skalare Gleichung in Matrizenform an. Dabei müssen wir
und erhalten
mit
- .
Mit der analytischen Lösung für w(ℓ) oben bleibt
mit
- .
Die seltsam anmutende Notation mit 1/2*1/30 hat seinen Sinn in der Anknüpfung an die Minimum Prinzipe und die Lösung der Gleichgewichtsbeziehungen.
% Matrizen besetzen
for i= 1:2
for j=1:2
E = conv(
polyder(polyder(phi(i,:))),
polyder(polyder(phi(j,:))))
I = polyint(E)
A(i,j) = diff(polyval(I,[0 1]))
end
b(i,1) = diff(polyval(polyint(
conv([-1,1],phi(i,:))),
[0 1]))
end
Equilibrium Conditions
Diese Gleichung erfüllt die Gleichgewichtsbedingungen
- ,
wenn
- .
% left blank intentionally
Solving
Das lineare Gleichungssystem löst in Matlab der Befehl
linsolve(.,.)für uns.

Hier ist
und wir sehen: unser Wunsch
von oben ist sogar exakt - nicht nur näherungsweise - erfüllt!
% nach x (W[2],W[3]) lösen
x = linsolve(A/30,b)
Post-Processing
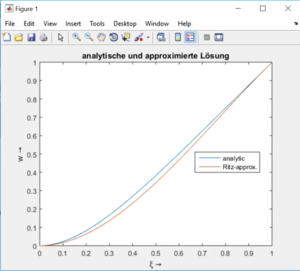
Die Näherungslösung und die analytische Lösung können wir jetzt im Vergleich auftragen:
% … und plotten
% analytische Ösung
a = [-1,5,-10,+10,0,0]/4.
% genäherte Lösung in Teilen
w = [x(1)*phi(1,:);
x(2)*phi(2,:)]
xi = linspace(0,1,100)
p = [polyval(a,xi);
polyval(w(1,:),xi);
polyval(w(2,:),xi)]
fig = plot(xi,p(1,:),xi,p(2,:)+p(3,:))
title('analytische und approximierte Lösung')
xlabel('ξ →')
ylabel('w →')
legend('analytic','Ritz-approx.')
Links
- ...
Literature
- ...