Sources/Lexikon/Dehnstab: Unterschied zwischen den Versionen
Die Seite wurde neu angelegt: „g“ |
Keine Bearbeitungszusammenfassung |
||
| (Eine dazwischenliegende Version desselben Benutzers wird nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
Der Dehnstab ist ein Stabmodell für den einachsigen Spannungszustand. Die einzige auftretenden Spannung ist ''σ<sub>xx</sub>'', also | |||
::<math>\displaystyle \underline{\sigma}=\left(\begin{array}{c}\sigma_{xx}\\0\\0\\0\\0\\0\end{array}\right)</math> | |||
Die Schnittlast ''N'' am Querschnitt mit dem Flächeninhalt ''A'' ist also | |||
::<math>N(x) = A\cdot\sigma_{xx}(x)</math> | |||
Aus den [[Sources/Lexikon/Spannungs-Dehnungs-Beziehung (Stress-Strain-Relation)|Spannungs-Dehnungs-Beziehung]] lesen wir außerdem | |||
::<math>\sigma_{xx} = E\cdot\varepsilon_{xx}</math> | |||
ab, also | |||
::<math>N = E\,A \cdot \varepsilon</math> | |||
Die Spannungen über den Querschnitt sind konstant, wir brauchen also nur eine einzige Ortskoordinate ''x'', um die Spannungen - und damit die Dehnungen und Verschiebungen - eindeutig zu beschreiben. Mit der [[Sources/Lexikon/Verzerrungs-Verschiebungs-Beziehung (Strain-Displacement-Relation)|Verzerrungs-Verschiebungs-Beziehung]] ''ε = u''' ist dann | |||
::<math>N = E\,A \cdot u'</math> | |||
[[Datei:Dehnstab-01.png|mini|Koordinaten]] | |||
Die Bedingung für das Kräfte-Gleichgewicht am Dehnstab lesen wir aus dem verformten System an, dabei ist ''n'' eine eingeprägte Streckenlast. | |||
::<math>N(x+\Delta x, t) - N(x) = n(x)\cdot \Delta x</math> | |||
Nach Dividion durch ''Δx'' und dem Übergang vom Differenzenquotienten zum Differentialquotienten ist | |||
::<math>N' = -n</math> | |||
Und somit - falls ''E, A'' nicht von ''x'' abhängen | |||
::<math>E\,A\, u'' = -n</math> | |||
Aktuelle Version vom 20. April 2021, 08:52 Uhr
Der Dehnstab ist ein Stabmodell für den einachsigen Spannungszustand. Die einzige auftretenden Spannung ist σxx, also
Die Schnittlast N am Querschnitt mit dem Flächeninhalt A ist also
Aus den Spannungs-Dehnungs-Beziehung lesen wir außerdem
ab, also
Die Spannungen über den Querschnitt sind konstant, wir brauchen also nur eine einzige Ortskoordinate x, um die Spannungen - und damit die Dehnungen und Verschiebungen - eindeutig zu beschreiben. Mit der Verzerrungs-Verschiebungs-Beziehung ε = u' ist dann
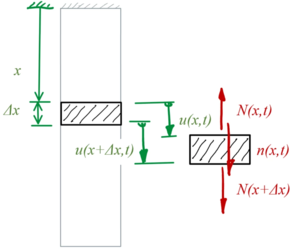
Die Bedingung für das Kräfte-Gleichgewicht am Dehnstab lesen wir aus dem verformten System an, dabei ist n eine eingeprägte Streckenlast.
Nach Dividion durch Δx und dem Übergang vom Differenzenquotienten zum Differentialquotienten ist
Und somit - falls E, A nicht von x abhängen