Gelöste Aufgaben/Kw29: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| (Eine dazwischenliegende Version desselben Benutzers wird nicht angezeigt) | |||
| Zeile 8: | Zeile 8: | ||
In einer Sporthalle wird ein Federball (Punktmasse ''m'') mit einer Anfangsgeschwindigkeit ''v<sub>0</sub>'' unter einem Winkel ''α'' gegenüber der Horizontalen abgeschlagen. Der Strömungswiderstand des Federballs wird mit | In einer Sporthalle wird ein Federball (Punktmasse ''m'') mit einer Anfangsgeschwindigkeit ''v<sub>0</sub>'' unter einem Winkel ''α'' gegenüber der Horizontalen abgeschlagen. Der Strömungswiderstand des Federballs wird mit | ||
::<math>W = \gamma\cdot v^2</math> | ::<math>\tilde{W} = \gamma\cdot v^2</math> | ||
angegeben, dabei ist ''γ'' eine gemessene Größe.<onlyinclude> | angegeben, dabei ist ''γ'' eine gemessene Größe.<onlyinclude> | ||
| Zeile 53: | Zeile 53: | ||
Die Bewegungsgleichungen in horizontale und vertikale Richtung sind | Die Bewegungsgleichungen in horizontale und vertikale Richtung sind | ||
::<math>\begin{array}{ll}m\;\ddot{u} + W\cdot \cos(\alpha) &= 0\\m\;\ddot{w} + W\cdot \sin(\alpha) &= -m\,g\end{array}</math>. | ::<math>\begin{array}{ll}m\;\ddot{u} + \tilde{W}\cdot \cos(\alpha) &= 0\\m\;\ddot{w} + \tilde{W}\cdot \sin(\alpha) &= -m\,g\end{array}</math>. | ||
Dabei ist | Dabei ist | ||
Aktuelle Version vom 28. Mai 2024, 06:43 Uhr
Aufgabenstellung
In einer Sporthalle wird ein Federball (Punktmasse m) mit einer Anfangsgeschwindigkeit v0 unter einem Winkel α gegenüber der Horizontalen abgeschlagen. Der Strömungswiderstand des Federballs wird mit
angegeben, dabei ist γ eine gemessene Größe.
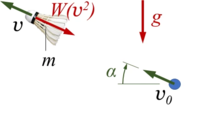
Schreiben Sie die Bewegungsgleichung des Federballs an. Formulieren Sie die Bewegungsgleichung des Federballs in dimensionsloser Form und berechnen Sie die Lösung numerisch als Anfangswertproblem.
Gegeben: g, m, γ, v0
Lösung mit Maxima
Header
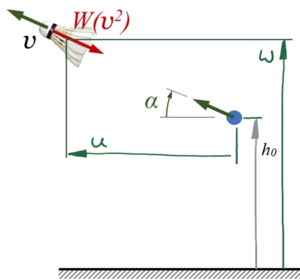
Die Koordinaten der Bewegung des Federballs sind
- u(t) in horizontale und
- w(t) in vertikale Richtung.
Als Parameter der Bewegung wählen wir:
.
/*********************************************************/
/* MAXIMA script */
/* version: wxMaxima 15.08.2 */
/* author: Andreas Baumgart */
/* last updated: 2018-12-02 */
/* ref: Kw28 (TM-C, Labor 5) */
/* description: finds the solution for */
/* the nonlinear IVP */
/*********************************************************/
/*********************************************************/
/* declare parameters */
params: [h[0] = 2*m, g = 10*m/s^2, v[0]=65*1000*m/3600/s];
Equilibrium Conditions
Die Bewegungsgleichungen in horizontale und vertikale Richtung sind
- .
Dabei ist
- .
Als nächstes machen wir die Bewegungsgleichungen dimensionslos mit
- der dimensionslosen Zeit und
- den dimensionslosen Koordinaten ,
dabei sind T = h0 / v0 die Bezugszeit und L = h0' die Bezugslänge.
Die neuen Form der nichtlinearen Bewegungsgleichung ergibt sich dann zu
- ,
die wir numerisch lösen.
/********************************/
/* define ODE in dim'less coordinates U */
/* equlilbrium condition */
eom : [m*'diff(u,t,2) = -gamma*v^2*cos(alpha),
m*'diff(w,t,2) = -gamma*v^2*sin(alpha) - m*g];
dimless: ['diff(u,t,2) = L*'diff(U,tau,2)/T^2,
'diff(w,t,2) = L*'diff(W,tau,2)/T^2,
v^2 = v[0]^2*nu^2, g=G*L/T^2, gamma = Gamma*m*L/T^2/v[0]^2,
nu^2 = 'diff(U,tau)^2+'diff(W,tau)^2,
sin(alpha) = 'diff(W,tau)/sqrt('diff(U,tau)^2+'diff(W,tau)^2), cos(alpha) = 'diff(U,tau)/sqrt('diff(U,tau)^2+'diff(W,tau)^2)];
eom : expand(subst(dimless,T^2*eom/L/m));
Solving
Für Γ=1/2 und α0 = 30° lösen wir das Problem numerisch, dazu wählen wir als Anfangsbedingungen
- .
/********************************/
/* numerical solution of IVP */
numpars: [L = h[0], T=h[0]/v[0], Gamma = 1];
numpars : append(numpars,subst(params,subst(numpars, subst(params,solve(dimless[4],G)))));
times : subst([t0 = 0, tmax = 20, dt = 0.01],
[t, t0, tmax, dt]);
dgl1stOrder : subst(numpars,[VU,VW,rhs(eom[1]),rhs(eom[2])]);
dgl1stOrder : subst(['diff(U,tau,1)=VU, 'diff(W,tau,1)=VW],dgl1stOrder);
stateVabs : [U,W,VU,VW];
initiVals : [0,1,cos(%pi/6),sin(%pi/6)];
ivs : rk(dgl1stOrder, stateVabs, initiVals, times)$
Post-Processing
Die Flugbahn des Federballs erhalten durch den Parameter-Plot mit W(τ) über U(τ).
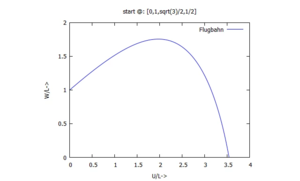
/********************************/
/* plot time functions */
/* solution samples */
Ti : makelist(ivs[j][1],j,1,length(ivs))$
Hi : [makelist(ivs[j][2],j,1,length(ivs)),
makelist(ivs[j][3],j,1,length(ivs))]$
Vi : [makelist(ivs[j][4],j,1,length(ivs)),
makelist(ivs[j][5],j,1,length(ivs))]$
/* parametric plot */
plot2d([discrete, Hi[1], Hi[2]],
[legend, "Flugbahn"],
[title, sconcat("start @: ",string(initiVals))],
[y,0,2],
[xlabel,"U/L->"], [ylabel,"W/L->"]);
Links
- ...
Literature
- ...