Gelöste Aufgaben/ODE1

Aufgabenstellung

Hier untersuchen wir systematisch ein System aus einem starren Pendel im Erdschwerefeld.

Lageplan

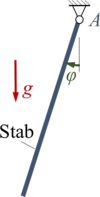
Gesucht sind Gleichgewichtslagen, Schwingungen um diese und die numerische Lösung der nichtlinearen Bewegungsgleichung.

Lösung mit Maxima

Header

Wir nehemn an: das Massenmoment des homogenen Stabes bzgl. A ist J_A, der Schwerpunkt des Stabes liegt in seiner Mitte.

/*******************************************************/
/* MAXIMA script                                       */
/* version: wxMaxima 15.08.2                           */
/* author: Andreas Baumgart                            */
/* last updated:                                       */
/* ref: TM-C                                           */
/* description: solve the IVP, check for stability     */
/*******************************************************/

Declarations

Aus dem Prinzip der virtuellen Verrückungen kommt die Gleichgewichtsbeziehung für den Stab:

$\delta W=\displaystyle \underbrace {-J_{A}\cdot {\ddot {\varphi }}\cdot \delta \varphi -m\cdot g\cdot {\frac {\ell }{2}}\cdot \sin(\varphi )\cdot \delta \varphi } _{\displaystyle =\delta W^{a}}-\underbrace {0} _{\displaystyle =\delta \Pi }$,

wobei

$\varphi =\varphi (t)$.

Mit der neuen, dimensionslosen Zeit

$\tau =\displaystyle {\frac {t}{t_{Bez}}}{\text{ und }}t_{Bez}^{2}={\frac {J_{A}}{m\cdot g\cdot {\frac {\ell }{2}}}}$

wird aus der Bewegungsgleichung

$\displaystyle {\frac {d^{2}}{d\tau ^{2}}}(\varphi )+\sin(\varphi )=0$.

/* parameter */ 
params: [t[Bez]^2=J/(m*g*l/2)]; 


/* dimensionless equations of motion */ 
ode: J*'diff(phi,tau,2)/t[Bez]^2+m*g*l/2*sin(phi)=0; 
ode: expand(subst(params,ode*(t[Bez]^2/J)));

Equilibrium Conditions

Die Gleichung

$\displaystyle {\frac {d^{2}}{d\tau ^{2}}}\varphi =0$

ist erfüllt für

$\sin(\varphi ){\stackrel {!}{=}}0{\text{, also }}\varphi =0,\pi ,2\,\pi ,\,\ldots$

Gleichgewichtslagen

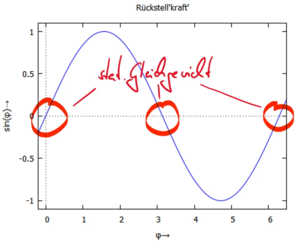
Die Funktion der Rückstell'kraft' sin(φ) schneidet die y-Achse dabei mit der Steigung +1 (z.B. bei φ₁ = 0, φ₃ = 2π) und mit der Steigung  -1 (z.B. bei φ₂ = π).

Das Vorzeichen der Steigung wird über die Stabilität der Lösung entscheiden!

/* static equilibrium conditions ....*/
plot2d(lhs(subst(['diff(phi,tau,2)=0],ode)), 
          [phi,-0.2,2*%pi+0.2], [title, "Rückstell'kraft'"], 
          [y,-1.1,1.1], [xlabel, "φ→"], [ylabel, "sin(φ)→"])$

Stability of Equilibrium Positions

Die Stabilität jeder Gleichgewichtsbedingung "im Kleinen" - also in unmittelbarer Umgebung der Gleichgewichtslage - untersuchen wir am linearisierten System.

Die Taylor-Reihenentwicklung um die Gleichgewichtslagen φ_i herum liefert

$\displaystyle {\frac {{d}^{2}}{d\,{{\tau }^{2}}}}\cdot \varphi _{i}+\underbrace {\sin \left(\varphi _{i}\right)} _{\displaystyle =0}+\underbrace {\cos \left(\varphi _{i}\right)} _{\displaystyle =+1/-1}\cdot \underbrace {\left(\varphi -\varphi _{i}\right)} _{\displaystyle :=\Delta \varphi _{i}}+{\mbox{...}}=0$

Dies ist Ausgangspunkt für unsere Stabilitätsanalyse:

Für φ₁ = 0 (= 2π ):

Der $e^{\lambda \;t}$ -Ansatz liefert

$\lambda _{1}^{2}=-1{\text{ also }}\lambda _{1}=\pm j\cdot \omega$,

also eine Schwingungslösung. Diese Lösung ist damit nicht instabil (weil wir keine Energiedissipation eingebaut haben, klingt sie aber auch nicht ab).

Für φ₃ = π):

Analog ist

$\lambda _{2}^{2}=+1{\text{ also }}\lambda _{2}=\pm 1$,

mit einer exponential abklingenden (λ₂=-1) und einer exponential aufklingenden (λ₂=+1) Lösung. Dieser zweite Anteil der Lösung macht sie instabil.

/* stability in proximity of equilib. conditions */
linode : taylor (ode, phi, Phi, 1);

Solving

Das nichtlineare Anfangswertproblem lösen wir durch numerische Integration.

Dafür müssen wir die Bewegungsgleichung als gewöhnliche Differentialgleichung (ODE) erster Ordnung schreiben, also mit

${\underline {y}}=\left({\begin{array}{c}\varphi \\\varphi '\end{array}}\right){\text{ und }}(.)':=\displaystyle {\frac {d}{d\tau }}(.)$

als

${\underline {y}}'=\left({\begin{array}{c}y_{1}\\-\sin(y_{2})\end{array}}\right)$.

Diese Bewegungsgleichung lösen wir mit den Anfangsbedingungen

${\underline {y}}(0):=\left({\begin{array}{c}\varphi '(0)\\0\end{array}}\right)$.

und das für verschiedene Anfangsgeschwindigkeiten y₁.

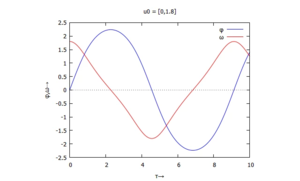
In der Nähe der stabilen Lösung finden wir periodische Lösungen:

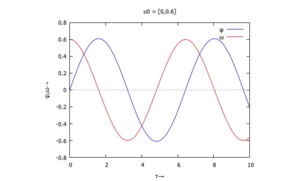Mit mehr "Anschwung" dreht die Stange "durch", die Lösung ist nicht mehr periodisch:

Lösung im Zeitbereich - die Stange "dreht durch".

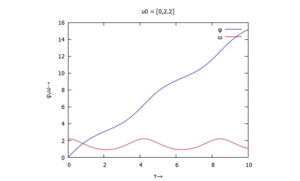
/* solve initial value problem */
dudt : [omega,rhs(solve(dgl,'diff(phi,tau,2))[1])];
time : [ t, 0, 10, 0.01 ];
u0: [[0,0.6],[0,1.8],[0,2.2]];
u : [phi,omega];
samples : [];
for i:1 thru length(u0) do
   (set : rk (dudt, u, u0[i], time ),
    set : [makelist(set[j][1],j,1,length(set)),
           makelist(set[j][2],j,1,length(set)),
           makelist(set[j][3],j,1,length(set))],
    samples : append(samples, set),
    headline : [title, simplode(["u0 = ",u0[i]])], 
    plot2d([[discrete,set[1],set[2]],
            [discrete,set[1],set[3]]],
            headline,  [legend, "φ","ω"],
            [xlabel, "τ→"],[ylabel, "φ,ω→"]))$

Post-Processing

Phasendiagramm

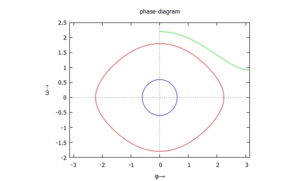
Diese Ergebnisse können wir im Phasendiagramm (Geschwindigkeit über der Auslenkung) auftragen.

/* phase diagram*/
toPlot : makelist([discrete,samples[3*(i-1)+2],
                            samples[3*(i-1)+3]],i,1,length(u0))$
plot2d(toPlot, [x,-%pi,+%pi], [legend, false],
                      [title, "phase-diagram"],
                      [xlabel, "φ→"],[ylabel, "ω→"])$

---

Links

• ...

Literature

• ...