Gelöste Aufgaben/Kw96: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
|||
| (2 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
[[Category:Gelöste Aufgaben]] | [[Category:Gelöste Aufgaben]] | ||
[[Category:Numerische Lösung]] | [[Category:Numerische Lösung]] | ||
[[Category:Randwertproblem]] | [[Category:Randwertproblem]] | ||
[[Category:Euler-Bernoulli-Balken]] | [[Category:Euler-Bernoulli-Balken]] | ||
[[Category:Finite-Differenzen-Methode]] | |||
[[Category:Maxima]] | [[Category:Maxima]] | ||
==Aufgabenstellung== | ==Aufgabenstellung== | ||
| Zeile 67: | Zeile 16: | ||
[[Datei:Kw98-02.png|mini|Systemparameter]] | [[Datei:Kw98-02.png|mini|Systemparameter]] | ||
Ermitteln Sie für ein Euler-Bernoulli-Modell die analytischen Verläufe der Schnittgrößen und Verschiebungen im Balken für die angegebenen Parameter: | Ermitteln Sie für ein Euler-Bernoulli-Modell die analytischen Verläufe der Schnittgrößen und Verschiebungen im Balken für die angegebenen Parameter: | ||
Die analytische Lösung finden Sie in Aufgabe [[Gelöste Aufgaben/Kw98|Kw98]]. | |||
== Lösung mit Maxima == | == Lösung mit Maxima == | ||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Header | {{MyCodeBlock|title=Header | ||
|text= | |text=Wir arbeiten mit den Standard-System-Matrizen nach Abschnitt "[[Sources/Anleitungen/FEM-Formulierung für den Euler-Bernoulli-Balken|FEM-Formulierung für den Euler-Bernoulli-Balken]]". | ||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
1 | /*******************************************************/ | ||
/* MAXIMA script */ | |||
/* version: wxMaxima 18.10.1 */ | |||
/* author: Andreas Baumgart */ | |||
/* last updated: 2019-02-10 */ | |||
/* ref: TM-C, Labor 4 */ | |||
/* description: finds the FE solution for */ | |||
/* lab problem #4 */ | |||
/*******************************************************/ | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Declarations | |||
|text= | |||
System-Parameter sind: | System-Parameter sind: | ||
<math>\begin{array}{l} \displaystyle {{q}_{A}}=3000 \frac{N}{m},\\ \displaystyle {\ell_{1}}=\frac{7\cdot m}{10},\\ \displaystyle {{\mathit{EI}}_{1}}=33600 N {{m}^{2}},\\ \displaystyle {\ell_{2}}=\frac{21}{40} m,\\ \displaystyle {{\mathit{EI}}_{2}}=16800 N {{m}^{2}},\\ \displaystyle {{K}_{A}}=96000 N m,\\ \displaystyle {{k}_{C}}=\frac{256}{229}\cdot {{k}_{B}},\\ \displaystyle {{k}_{B}}=\frac{256}{229} N m,\\ \displaystyle {{q}_{B}}=12000\frac{N}{m},\\ \displaystyle {{M}_{B}}=1470 N m \end{array}</math> | ::<math>\begin{array}{l} \displaystyle {{q}_{A}}=3000 \frac{N}{m},\\ \displaystyle {\ell_{1}}=\frac{7\cdot m}{10},\\ \displaystyle {{\mathit{EI}}_{1}}=33600 N {{m}^{2}},\\ \displaystyle {\ell_{2}}=\frac{21}{40} m,\\ \displaystyle {{\mathit{EI}}_{2}}=16800 N {{m}^{2}},\\ \displaystyle {{K}_{A}}=96000 N m,\\ \displaystyle {{k}_{C}}=\frac{256}{229}\cdot {{k}_{B}},\\ \displaystyle {{k}_{B}}=\frac{256}{229} N m,\\ \displaystyle {{q}_{B}}=12000\frac{N}{m},\\ \displaystyle {{M}_{B}}=1470 N m \end{array}</math>. | ||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
1 | /* declare variational variables - see 6.3 Identifiers */ | ||
declare("δA", alphabetic); | |||
declare("δΠ", alphabetic); | |||
declare("δW", alphabetic); | |||
declare("δΦ", alphabetic); | |||
declare("δw", alphabetic); | |||
declare( "ℓ", alphabetic); | |||
/* declarations */ | |||
assume(ℓ[i]>0); | |||
/* system parameter */ | |||
units : [mm = m/1000, cm = m/100]; | |||
params : [q[A]=3*N/mm, ℓ[1]=700*mm, EI[1] = 2.1*10^11*N/m^2 * 3*cm*(4*cm)^3/12]; | |||
simple : [ℓ[2] = 3/4*ℓ[1], EI[2] = EI[1]/2, | |||
K[A] = 2*EI[1]/ℓ[1], K[C] = 512/229*K[B]/2, K[B] = 2*EI[1]/ℓ[1]^3, | |||
q[B] = 4*q[A], M[B] = q[A]*ℓ[1]^2]; | |||
params : append(params,makelist( | |||
lhs(simple[i])=subst(params,rhs(simple[i])),i,1,length(simple))); | |||
params : subst(units,params); | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
== | <!--------------------------------------------------------------------------------> | ||
{{MyCodeBlock|title=Formfunctions | |||
|text=Die Ansatzfunktion für die Trial-Functions ist ein Polynom 3. Grades: | |||
::<math>\mathrm{w}\left( \xi\right) :={{c}_{3}}\cdot {{\xi}^{3}}+{{c}_{2}}\cdot {{\xi}^{2}}+{{c}_{1}}\cdot \xi+{{c}_{0}}</math> | |||
<math>\mathrm{w}\left( \xi\right) :={{c}_{3}}\cdot {{\xi}^{3}}+{{c}_{2}}\cdot {{\xi}^{2}}+{{c}_{1}}\cdot \xi+{{c}_{0}}</math> | |||
An den Rändern müssen die Auslenkung und Kippung mit den Knoten-Variablen übereinstimmen: | An den Rändern müssen die Auslenkung und Kippung mit den Knoten-Variablen übereinstimmen: | ||
<math>\begin{array}{l} \displaystyle {{c}_{0}}={{W}_{i-1}},\\ \displaystyle \frac{{{c}_{1}}}{{{l}_{i}}}={{\Phi}_{i-1}},\\ \displaystyle {{c}_{3}}+{{c}_{2}}+{{c}_{1}}+{{c}_{0}}={{W}_{i}},\\ \displaystyle \frac{{{c}_{1}}+2\cdot {{c}_{2}}+3\cdot {{c}_{3}}}{{{l}_{i}}}={{\Phi}_{i}} \end{array}</math>[[Datei:Kw96-11.png|alternativtext=Trial-Functions|mini|Trial-Functions]]Damit ist die Ansatzfunktion des Finiten Elements mit den vier Knotenvariablen | ::<math>\begin{array}{l} \displaystyle {{c}_{0}}={{W}_{i-1}},\\ \displaystyle \frac{{{c}_{1}}}{{{l}_{i}}}={{\Phi}_{i-1}},\\ \displaystyle {{c}_{3}}+{{c}_{2}}+{{c}_{1}}+{{c}_{0}}={{W}_{i}},\\ \displaystyle \frac{{{c}_{1}}+2\cdot {{c}_{2}}+3\cdot {{c}_{3}}}{{{l}_{i}}}={{\Phi}_{i}} \end{array}</math>[[Datei:Kw96-11.png|alternativtext=Trial-Functions|mini|Trial-Functions]]Damit ist die Ansatzfunktion des Finiten Elements mit den vier Knotenvariablen | ||
{{ | ::<math>w(\xi)\;=\; \ell_i \cdot \Phi_i \cdot \left( \xi-1 \right) \cdot \xi^2+W_{i-1} \cdot \left( \xi-1\right) ^2 \cdot \left( 1+2 \cdot \xi\right)-W_i \cdot \xi^2 \cdot \left( 2\cdot \xi-3\right) +\Phi_{i-1} \cdot \ell_i \cdot \left( \xi-1\right) ^2 \cdot \xi</math>. | ||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
1 | /**** define form functions ***/ | ||
/* coordinates */ | |||
coords : [[ W[i-1], Φ[i-1], W[i], Φ[i]], | |||
[δW[i-1],δΦ[i-1],δW[i],δΦ[i]]]; | |||
/* generic polynomials */ | |||
define(w(xi),sum(c[i]*xi^(i),i,0,3)); | |||
/* … and boundary conditions */ | |||
bc : [w(0) = W[i-1], | |||
subst([xi=0],diff(w(xi),xi)/ℓ[i])=Φ[i-1], | |||
w(1) = W[i], | |||
subst([xi=1],diff(w(xi),xi)/ℓ[i])=Φ[i]]; | |||
/* solve for c's to comply with geometric boundary conditions */ | |||
coeffs : solve(bc, makelist(c[i],i,0,3))[1]; | |||
print("w(ξ) = ",facsum(expand(subst(coeffs,w(xi))),coords[1])); | |||
trialfcts: makelist(phi[i]=coeff(expand(subst(coeffs,w(xi))),coords[1][i]),i,1,4); | |||
plot2d(subst([ℓ[i]=5],subst(trialfcts,makelist(phi[i],i,1,4))), | |||
[xi,0,1],[xlabel,"ξ/1 →"], | |||
[legend,"φ1","5*φ2/ℓ","φ3","5*φ4/ℓ"]); | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
== | <!--------------------------------------------------------------------------------> | ||
{{MyCodeBlock|title=Equilibrium Conditions | |||
|text= | |||
So sind die Element-Steifigkeitsmatrix | So sind die Element-Steifigkeitsmatrix | ||
<math>\displaystyle \underline{\underline{K}}_i=\,\frac{EI_i}{\ell_i^3}\begin{pmatrix}12 & 6\cdot {{\ell}_{i}} & -12 & 6\cdot {{\ell}_{i}}\\ 6\cdot {{\ell}_{i}} & 4\cdot {{\ell}_{i}^{2}} & -6\cdot {{\ell}_{i}} & 2\cdot {{\ell}_{i}^{2}}\\ -12 & -6\cdot {{\ell}_{i}} & 12 & -6\cdot {{\ell}_{i}}\\ 6\cdot {{\ell}_{i}} & 2\cdot {{\ell}_{i}^{2}} & -6\cdot {{\ell}_{i}} & 4\cdot {{\ell}_{i}^{2}}\end{pmatrix}</math> | ::<math>\displaystyle \underline{\underline{K}}_i=\,\frac{EI_i}{\ell_i^3}\begin{pmatrix}12 & 6\cdot {{\ell}_{i}} & -12 & 6\cdot {{\ell}_{i}}\\ 6\cdot {{\ell}_{i}} & 4\cdot {{\ell}_{i}^{2}} & -6\cdot {{\ell}_{i}} & 2\cdot {{\ell}_{i}^{2}}\\ -12 & -6\cdot {{\ell}_{i}} & 12 & -6\cdot {{\ell}_{i}}\\ 6\cdot {{\ell}_{i}} & 2\cdot {{\ell}_{i}^{2}} & -6\cdot {{\ell}_{i}} & 4\cdot {{\ell}_{i}^{2}}\end{pmatrix}</math> | ||
die Koordinaten des FE-Modells - hier für das Element "1": | die Koordinaten des FE-Modells - hier für das Element "1": | ||
<math>\underline{Q}\,=\,\begin{pmatrix}{{\Phi}_{0}}\\ {{W}_{1}}\\ {{\Phi}_{1}}\\ {{W}_{2}}\end{pmatrix}</math>. | ::<math>\underline{Q}\,=\,\begin{pmatrix}{{\Phi}_{0}}\\ {{W}_{1}}\\ {{\Phi}_{1}}\\ {{W}_{2}}\end{pmatrix}</math>. | ||
Wir komponieren daraus die System-Steifigkeitsmatrix - durch Aufaddieren der Beiträge der beiden Elemente und Einarbeiten der Randbedingugnen - zu | Wir komponieren daraus die System-Steifigkeitsmatrix - durch Aufaddieren der Beiträge der beiden Elemente und Einarbeiten der Randbedingugnen - zu | ||
<math>\underline{\underline{K}}_0 =\begin{pmatrix} {K_A}+\frac{4 {{\mathit{EI}}_1}}{{\ell_1}} & -\frac{6 {{\mathit{EI}}_1}}{{{\ell}_{1}^{2}}} & \frac{2 {{\mathit{EI}}_1}}{{\ell_1}} & 0\\ -\frac{6 {{\mathit{EI}}_1}}{{{\ell}_{1}^{2}}} & {k_B}+\frac{12 {{\mathit{EI}}_2}}{{{\ell}_{2}^{3}}}+\frac{12 {{\mathit{EI}}_1}}{{{\ell}_{1}^{3}}} & \frac{6 {{\mathit{EI}}_2}}{{{\ell}_{2}^{2}}}-\frac{6 {{\mathit{EI}}_1}}{{{\ell}_{1}^{2}}} & -\frac{12 {{\mathit{EI}}_2}}{{{\ell}_{2}^{3}}}\\ \frac{2 {{\mathit{EI}}_1}}{{\ell_1}} & \frac{6 {{\mathit{EI}}_2}}{{{\ell}_{2}^{2}}}-\frac{6 {{\mathit{EI}}_1}}{{{\ell}_{1}^{2}}} & \frac{4 {{\mathit{EI}}_2}}{{\ell_2}}+\frac{4 {{\mathit{EI}}_1}}{{\ell_1}} & -\frac{6 {{\mathit{EI}}_2}}{{{\ell}_{2}^{2}}}\\ 0 & -\frac{12 {{\mathit{EI}}_2}}{{{\ell}_{2}^{3}}} & -\frac{6 {{\mathit{EI}}_2}}{{{\ell}_{2}^{2}}} & {k_C}+\frac{12 {{\mathit{EI}}_2}}{{{\ell}_{2}^{3}}}\end{pmatrix}</math> | ::<math>\underline{\underline{K}}_0 =\begin{pmatrix} {K_A}+\frac{4 {{\mathit{EI}}_1}}{{\ell_1}} & -\frac{6 {{\mathit{EI}}_1}}{{{\ell}_{1}^{2}}} & \frac{2 {{\mathit{EI}}_1}}{{\ell_1}} & 0\\ -\frac{6 {{\mathit{EI}}_1}}{{{\ell}_{1}^{2}}} & {k_B}+\frac{12 {{\mathit{EI}}_2}}{{{\ell}_{2}^{3}}}+\frac{12 {{\mathit{EI}}_1}}{{{\ell}_{1}^{3}}} & \frac{6 {{\mathit{EI}}_2}}{{{\ell}_{2}^{2}}}-\frac{6 {{\mathit{EI}}_1}}{{{\ell}_{1}^{2}}} & -\frac{12 {{\mathit{EI}}_2}}{{{\ell}_{2}^{3}}}\\ \frac{2 {{\mathit{EI}}_1}}{{\ell_1}} & \frac{6 {{\mathit{EI}}_2}}{{{\ell}_{2}^{2}}}-\frac{6 {{\mathit{EI}}_1}}{{{\ell}_{1}^{2}}} & \frac{4 {{\mathit{EI}}_2}}{{\ell_2}}+\frac{4 {{\mathit{EI}}_1}}{{\ell_1}} & -\frac{6 {{\mathit{EI}}_2}}{{{\ell}_{2}^{2}}}\\ 0 & -\frac{12 {{\mathit{EI}}_2}}{{{\ell}_{2}^{3}}} & -\frac{6 {{\mathit{EI}}_2}}{{{\ell}_{2}^{2}}} & {k_C}+\frac{12 {{\mathit{EI}}_2}}{{{\ell}_{2}^{3}}}\end{pmatrix}</math> | ||
Wie das geht, steht in Abschnitt [[Randwertprobleme/Methoden zur Lösung von Randwertproblemen/Finite Elemente Methode|Finite Elemente Methode]].< | Wie das geht, steht in Abschnitt [[Randwertprobleme/Methoden zur Lösung von Randwertproblemen/Finite Elemente Methode|Finite Elemente Methode]]. | ||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
/********************************************/ | |||
/* EUILIBRIUM CONDITIONS */ | |||
/* generic stiffness matrix */ | |||
K[i] : EI[i]/ℓ[i]^3*makelist(makelist( | |||
integrate( | |||
'diff(phi[i],xi,2)*'diff(phi[j],xi,2), | |||
xi,0,1), | |||
j,1,4),i,1,4); | |||
K[i] : subst(trialfcts,K[i]); | |||
K[i] : ev(K[i],nouns); | |||
K[i] : funmake('matrix,K[i]); | |||
/* compose system matrix */ | |||
NoN : 3; /* Number of Nodes*/ | |||
K[0] : zeromatrix(2*NoN,2*NoN); | |||
for m:1 thru 4 do | |||
for n:1 thru 4 do | |||
(K[0][ m, n] : K[0][ m, n] + subst([i=1],K[i][m,n]), | |||
K[0][2+m,2+n] : K[0][2+m,2+n] + subst([i=2],K[i][m,n])); | |||
/* add springs */ | |||
K[0][2,2] : K[0][2,2] + K[A]; /* Φ[0] */ | |||
K[0][3,3] : K[0][3,3] + K[B]; /* W[1] */ | |||
K[0][5,5] : K[0][5,5] + K[C]; /* W[2] */ | |||
Q : matrix([W[0]],[Φ[0]],[W[1]],[Φ[1]],[W[2]],[Φ[2]]); | |||
/* incorporate geometric boundary conditions */ | |||
/* eliminate rows / columns for W[0], Φ[2] (positions 1, 6) */ | |||
K[0] : submatrix(1,submatrix(6,K[0],6),1); | |||
Q : submatrix(1,submatrix(6,Q)); | |||
/* compose righ-hand-side */ | |||
P : transpose(funmake('matrix, | |||
[subst([i=1],append(makelist(integrate( | |||
ℓ[i]*subst(trialfcts,(q[A]*(1-xi)+q[B]*xi)*phi[j]), | |||
xi,0,1),j,1,4),[0,0]))] | |||
)); | |||
P[4,1] : P[4,1]+M[B]; | |||
/* eliminate BCs */ | |||
P : submatrix(1,6,P); | |||
print('K[i]," = ",EI[i]/ℓ[i]^3, ratsimp(K[i]/(EI[i]/ℓ[i]^3)))$ | |||
print('K[0]," = ", K[0])$ | |||
print("Q = ", Q)$ | |||
print("P = ", P)$ | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
== | <!--------------------------------------------------------------------------------> | ||
{{MyCodeBlock|title=Solving | |||
|text= | |||
Die Knotenvariablen sind damit | Die Knotenvariablen sind damit | ||
<math>\begin{array}{ll}W_0 = 0& \\\Phi_0 = 0.00624& \\W_1 = 0.00657 m& \\\Phi_1 = 0.0123& \\W_2 = 0.00846 m& \\\Phi_2 = 0& \end{array}</math> | ::<math>\begin{array}{ll}W_0 = 0& \\\Phi_0 = 0.00624& \\W_1 = 0.00657 m& \\\Phi_1 = 0.0123& \\W_2 = 0.00846 m& \\\Phi_2 = 0& \end{array}</math>. | ||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
1 | /********************************************/ | ||
/* SOLVE */ | |||
fpprintprec: 3; | |||
sol[1] : linsolve_by_lu(subst(params,K[0]),subst(params,P))[1]; | |||
sol[1] : append([W[0]=0],makelist(Q[i][1] = sol[1][i][1],i,1,4), [Φ[2]=0]); | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
<!--------------------------------------------------------> | |||
{{MyCodeBlock|title=Post-Processing | {{MyCodeBlock|title=Post-Processing | ||
|text= | |||
|text= | [[Datei:Kw96-21.png|mini|Biegelinie ''w(x)''|ohne]] | ||
Die Biegelinie des Balkens sieht damit so aus: | |||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
1+1 | /********************************************/ | ||
/* POSTPROCESS */ | |||
/* user parametric plot- hence t as independant variable */ | |||
f1 : subst([xi=t],subst(params,expand(subst(sol[1],subst([i=1],subst(coeffs,w(xi))))))); | |||
f2 : subst([xi=t],subst(params,expand(subst(sol[1],subst([i=2],subst(coeffs,w(xi))))))); | |||
scale : subst(params,(ℓ[2]/ℓ[1])); | |||
plot2d([[parametric, t, f1/m, [t, 0, 1]], | |||
[parametric, 1+t*scale, f2/m, [t, 0, 1]]], | |||
[gnuplot_preamble, "set yrange [] reverse"], | |||
[legend, "sec. I", "sec. II"], | |||
[xlabel, "x/ℓ[1] →"], | |||
[ylabel, "← w/m"])$ | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
<hr/> | <hr/> | ||
'''Links''' | '''Links''' | ||
* | * Analytische Lösung des Problems: [[Gelöste Aufgaben/Kw98|Kw98]] | ||
'''Literature''' | '''Literature''' | ||
* ... | * ... | ||
Aktuelle Version vom 31. März 2021, 13:48 Uhr
Aufgabenstellung
Ein Stab ABC ist durch eine lineare veränderliche Streckenlast q mit den Eckwerten qA in A und qB in B sowie dem Moment MB in B belastet. Der Stab (E-Modul: E) besteht aus zwei Sektionen mit den Längen l1 bzw. l2 sowie den Flächenmomenten I1 bzw. I2. Der Stab ist in A durch ein gelenkiges Festlager, in C durch eine Schiebehülse gelagert, in B sind die beiden Sektionen fest miteinander verbunden. Die Feder in A ist eine Drehfester mit Steifigkeit KA, die Federn in B und C sind Translationsfedern mit den Steifigkeiten kB, kC.
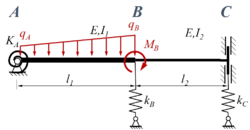
Gesucht ist die FEM Lösung für den Euler-Bernoulli-Balken unter Verwendung von zwei Finiten Elementen.
Ermitteln Sie für ein Euler-Bernoulli-Modell die analytischen Verläufe der Schnittgrößen und Verschiebungen im Balken für die angegebenen Parameter:
Die analytische Lösung finden Sie in Aufgabe Kw98.
Lösung mit Maxima
Header
Wir arbeiten mit den Standard-System-Matrizen nach Abschnitt "FEM-Formulierung für den Euler-Bernoulli-Balken".
/*******************************************************/
/* MAXIMA script */
/* version: wxMaxima 18.10.1 */
/* author: Andreas Baumgart */
/* last updated: 2019-02-10 */
/* ref: TM-C, Labor 4 */
/* description: finds the FE solution for */
/* lab problem #4 */
/*******************************************************/
Declarations
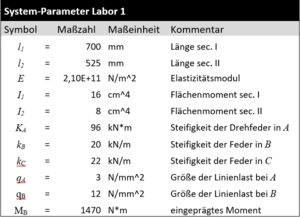
System-Parameter sind:
- .
/* declare variational variables - see 6.3 Identifiers */
declare("δA", alphabetic);
declare("δΠ", alphabetic);
declare("δW", alphabetic);
declare("δΦ", alphabetic);
declare("δw", alphabetic);
declare( "ℓ", alphabetic);
/* declarations */
assume(ℓ[i]>0);
/* system parameter */
units : [mm = m/1000, cm = m/100];
params : [q[A]=3*N/mm, ℓ[1]=700*mm, EI[1] = 2.1*10^11*N/m^2 * 3*cm*(4*cm)^3/12];
simple : [ℓ[2] = 3/4*ℓ[1], EI[2] = EI[1]/2,
K[A] = 2*EI[1]/ℓ[1], K[C] = 512/229*K[B]/2, K[B] = 2*EI[1]/ℓ[1]^3,
q[B] = 4*q[A], M[B] = q[A]*ℓ[1]^2];
params : append(params,makelist(
lhs(simple[i])=subst(params,rhs(simple[i])),i,1,length(simple)));
params : subst(units,params);
Formfunctions
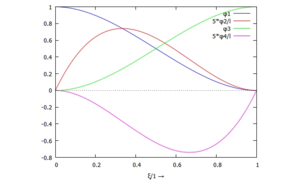
Die Ansatzfunktion für die Trial-Functions ist ein Polynom 3. Grades:
An den Rändern müssen die Auslenkung und Kippung mit den Knoten-Variablen übereinstimmen:
- .
/**** define form functions ***/
/* coordinates */
coords : [[ W[i-1], Φ[i-1], W[i], Φ[i]],
[δW[i-1],δΦ[i-1],δW[i],δΦ[i]]];
/* generic polynomials */
define(w(xi),sum(c[i]*xi^(i),i,0,3));
/* … and boundary conditions */
bc : [w(0) = W[i-1],
subst([xi=0],diff(w(xi),xi)/ℓ[i])=Φ[i-1],
w(1) = W[i],
subst([xi=1],diff(w(xi),xi)/ℓ[i])=Φ[i]];
/* solve for c's to comply with geometric boundary conditions */
coeffs : solve(bc, makelist(c[i],i,0,3))[1];
print("w(ξ) = ",facsum(expand(subst(coeffs,w(xi))),coords[1]));
trialfcts: makelist(phi[i]=coeff(expand(subst(coeffs,w(xi))),coords[1][i]),i,1,4);
plot2d(subst([ℓ[i]=5],subst(trialfcts,makelist(phi[i],i,1,4))),
[xi,0,1],[xlabel,"ξ/1 →"],
[legend,"φ1","5*φ2/ℓ","φ3","5*φ4/ℓ"]);
Equilibrium Conditions
So sind die Element-Steifigkeitsmatrix
die Koordinaten des FE-Modells - hier für das Element "1":
- .
Wir komponieren daraus die System-Steifigkeitsmatrix - durch Aufaddieren der Beiträge der beiden Elemente und Einarbeiten der Randbedingugnen - zu
Wie das geht, steht in Abschnitt Finite Elemente Methode.
/********************************************/
/* EUILIBRIUM CONDITIONS */
/* generic stiffness matrix */
K[i] : EI[i]/ℓ[i]^3*makelist(makelist(
integrate(
'diff(phi[i],xi,2)*'diff(phi[j],xi,2),
xi,0,1),
j,1,4),i,1,4);
K[i] : subst(trialfcts,K[i]);
K[i] : ev(K[i],nouns);
K[i] : funmake('matrix,K[i]);
/* compose system matrix */
NoN : 3; /* Number of Nodes*/
K[0] : zeromatrix(2*NoN,2*NoN);
for m:1 thru 4 do
for n:1 thru 4 do
(K[0][ m, n] : K[0][ m, n] + subst([i=1],K[i][m,n]),
K[0][2+m,2+n] : K[0][2+m,2+n] + subst([i=2],K[i][m,n]));
/* add springs */
K[0][2,2] : K[0][2,2] + K[A]; /* Φ[0] */
K[0][3,3] : K[0][3,3] + K[B]; /* W[1] */
K[0][5,5] : K[0][5,5] + K[C]; /* W[2] */
Q : matrix([W[0]],[Φ[0]],[W[1]],[Φ[1]],[W[2]],[Φ[2]]);
/* incorporate geometric boundary conditions */
/* eliminate rows / columns for W[0], Φ[2] (positions 1, 6) */
K[0] : submatrix(1,submatrix(6,K[0],6),1);
Q : submatrix(1,submatrix(6,Q));
/* compose righ-hand-side */
P : transpose(funmake('matrix,
[subst([i=1],append(makelist(integrate(
ℓ[i]*subst(trialfcts,(q[A]*(1-xi)+q[B]*xi)*phi[j]),
xi,0,1),j,1,4),[0,0]))]
));
P[4,1] : P[4,1]+M[B];
/* eliminate BCs */
P : submatrix(1,6,P);
print('K[i]," = ",EI[i]/ℓ[i]^3, ratsimp(K[i]/(EI[i]/ℓ[i]^3)))$
print('K[0]," = ", K[0])$
print("Q = ", Q)$
print("P = ", P)$
Solving
Die Knotenvariablen sind damit
- .
/********************************************/
/* SOLVE */
fpprintprec: 3;
sol[1] : linsolve_by_lu(subst(params,K[0]),subst(params,P))[1];
sol[1] : append([W[0]=0],makelist(Q[i][1] = sol[1][i][1],i,1,4), [Φ[2]=0]);
Post-Processing
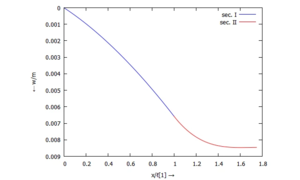
Die Biegelinie des Balkens sieht damit so aus:
/********************************************/
/* POSTPROCESS */
/* user parametric plot- hence t as independant variable */
f1 : subst([xi=t],subst(params,expand(subst(sol[1],subst([i=1],subst(coeffs,w(xi)))))));
f2 : subst([xi=t],subst(params,expand(subst(sol[1],subst([i=2],subst(coeffs,w(xi)))))));
scale : subst(params,(ℓ[2]/ℓ[1]));
plot2d([[parametric, t, f1/m, [t, 0, 1]],
[parametric, 1+t*scale, f2/m, [t, 0, 1]]],
[gnuplot_preamble, "set yrange [] reverse"],
[legend, "sec. I", "sec. II"],
[xlabel, "x/ℓ[1] →"],
[ylabel, "← w/m"])$
Links
- Analytische Lösung des Problems: Kw98
Literature
- ...