Gelöste Aufgaben/Kw96: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| (6 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
[[Category:Gelöste Aufgaben]] | [[Category:Gelöste Aufgaben]] | ||
[[Category:Numerische Lösung]] | [[Category:Numerische Lösung]] | ||
[[Category:Randwertproblem]] | [[Category:Randwertproblem]] | ||
[[Category:Euler-Bernoulli-Balken]] | [[Category:Euler-Bernoulli-Balken]] | ||
[[Category:Finite-Differenzen-Methode]] | |||
[[Category:Maxima]] | [[Category:Maxima]] | ||
==Aufgabenstellung== | ==Aufgabenstellung== | ||
Ein Stab ''ABC'' ist durch eine lineare veränderliche Streckenlast ''q'' mit den Eckwerten ''q<sub>A</sub>'' in ''A'' und ''q<sub>B</sub>'' in ''B'' sowie dem Moment ''M<sub>B</sub>'' in ''B'' belastet. Der Stab (E-Modul: ''E'') besteht aus zwei Sektionen mit den Längen ''l<sub>1</sub>'' bzw. ''l<sub>2</sub>'' sowie den Flächenmomenten ''I<sub>1</sub>'' bzw. ''I<sub>2</sub>''. Der Stab ist in ''A'' durch ein gelenkiges Festlager, in ''C'' durch eine Schiebehülse gelagert, in ''B'' sind die beiden Sektionen fest miteinander verbunden. Die Feder in ''A'' ist eine Drehfester mit Steifigkeit ''K<sub>A</sub>'', die Federn in ''B'' und ''C'' sind Translationsfedern mit den Steifigkeiten ''k<sub>B</sub>, k<sub>C</sub>''. | |||
<onlyinclude> | <onlyinclude> | ||
[[Datei: | [[Datei:Kw98-01.png|alternativtext=|links|mini|250x250px|Lageplan]] | ||
Gesucht ist | Gesucht ist die FEM Lösung für den Euler-Bernoulli-Balken unter Verwendung von zwei Finiten Elementen. | ||
</onlyinclude> | </onlyinclude> | ||
[[Datei:Kw98-02.png|mini|Systemparameter]] | |||
Ermitteln Sie für ein Euler-Bernoulli-Modell die analytischen Verläufe der Schnittgrößen und Verschiebungen im Balken für die angegebenen Parameter: | |||
Die analytische Lösung finden Sie in Aufgabe [[Gelöste Aufgaben/Kw98|Kw98]]. | |||
== Lösung mit Maxima == | == Lösung mit Maxima == | ||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Header | {{MyCodeBlock|title=Header | ||
|text= | |text=Wir arbeiten mit den Standard-System-Matrizen nach Abschnitt "[[Sources/Anleitungen/FEM-Formulierung für den Euler-Bernoulli-Balken|FEM-Formulierung für den Euler-Bernoulli-Balken]]". | ||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
1 | /*******************************************************/ | ||
/* MAXIMA script */ | |||
/* version: wxMaxima 18.10.1 */ | |||
/* author: Andreas Baumgart */ | |||
/* last updated: 2019-02-10 */ | |||
/* ref: TM-C, Labor 4 */ | |||
/* description: finds the FE solution for */ | |||
/* lab problem #4 */ | |||
/*******************************************************/ | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Declarations | {{MyCodeBlock|title=Declarations | ||
|text= | |text= | ||
System-Parameter sind: | |||
::<math>\begin{array}{l} \displaystyle {{q}_{A}}=3000 \frac{N}{m},\\ \displaystyle {\ell_{1}}=\frac{7\cdot m}{10},\\ \displaystyle {{\mathit{EI}}_{1}}=33600 N {{m}^{2}},\\ \displaystyle {\ell_{2}}=\frac{21}{40} m,\\ \displaystyle {{\mathit{EI}}_{2}}=16800 N {{m}^{2}},\\ \displaystyle {{K}_{A}}=96000 N m,\\ \displaystyle {{k}_{C}}=\frac{256}{229}\cdot {{k}_{B}},\\ \displaystyle {{k}_{B}}=\frac{256}{229} N m,\\ \displaystyle {{q}_{B}}=12000\frac{N}{m},\\ \displaystyle {{M}_{B}}=1470 N m \end{array}</math>. | |||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
1 | /* declare variational variables - see 6.3 Identifiers */ | ||
declare("δA", alphabetic); | |||
declare("δΠ", alphabetic); | |||
declare("δW", alphabetic); | |||
declare("δΦ", alphabetic); | |||
declare("δw", alphabetic); | |||
declare( "ℓ", alphabetic); | |||
/* declarations */ | |||
assume(ℓ[i]>0); | |||
/* system parameter */ | |||
units : [mm = m/1000, cm = m/100]; | |||
params : [q[A]=3*N/mm, ℓ[1]=700*mm, EI[1] = 2.1*10^11*N/m^2 * 3*cm*(4*cm)^3/12]; | |||
simple : [ℓ[2] = 3/4*ℓ[1], EI[2] = EI[1]/2, | |||
K[A] = 2*EI[1]/ℓ[1], K[C] = 512/229*K[B]/2, K[B] = 2*EI[1]/ℓ[1]^3, | |||
q[B] = 4*q[A], M[B] = q[A]*ℓ[1]^2]; | |||
params : append(params,makelist( | |||
lhs(simple[i])=subst(params,rhs(simple[i])),i,1,length(simple))); | |||
params : subst(units,params); | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
<!--------------------------------------------------------------------------------> | <!--------------------------------------------------------------------------------> | ||
{{MyCodeBlock|title=Formfunctions | {{MyCodeBlock|title=Formfunctions | ||
|text= | |text=Die Ansatzfunktion für die Trial-Functions ist ein Polynom 3. Grades: | ||
::<math>\mathrm{w}\left( \xi\right) :={{c}_{3}}\cdot {{\xi}^{3}}+{{c}_{2}}\cdot {{\xi}^{2}}+{{c}_{1}}\cdot \xi+{{c}_{0}}</math> | |||
An den Rändern müssen die Auslenkung und Kippung mit den Knoten-Variablen übereinstimmen: | |||
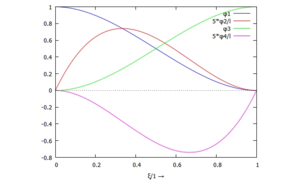
::<math>\begin{array}{l} \displaystyle {{c}_{0}}={{W}_{i-1}},\\ \displaystyle \frac{{{c}_{1}}}{{{l}_{i}}}={{\Phi}_{i-1}},\\ \displaystyle {{c}_{3}}+{{c}_{2}}+{{c}_{1}}+{{c}_{0}}={{W}_{i}},\\ \displaystyle \frac{{{c}_{1}}+2\cdot {{c}_{2}}+3\cdot {{c}_{3}}}{{{l}_{i}}}={{\Phi}_{i}} \end{array}</math>[[Datei:Kw96-11.png|alternativtext=Trial-Functions|mini|Trial-Functions]]Damit ist die Ansatzfunktion des Finiten Elements mit den vier Knotenvariablen | |||
::<math>w(\xi)\;=\; \ell_i \cdot \Phi_i \cdot \left( \xi-1 \right) \cdot \xi^2+W_{i-1} \cdot \left( \xi-1\right) ^2 \cdot \left( 1+2 \cdot \xi\right)-W_i \cdot \xi^2 \cdot \left( 2\cdot \xi-3\right) +\Phi_{i-1} \cdot \ell_i \cdot \left( \xi-1\right) ^2 \cdot \xi</math>. | |||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
1 | /**** define form functions ***/ | ||
/* coordinates */ | |||
coords : [[ W[i-1], Φ[i-1], W[i], Φ[i]], | |||
[δW[i-1],δΦ[i-1],δW[i],δΦ[i]]]; | |||
/* generic polynomials */ | |||
define(w(xi),sum(c[i]*xi^(i),i,0,3)); | |||
/* … and boundary conditions */ | |||
bc : [w(0) = W[i-1], | |||
subst([xi=0],diff(w(xi),xi)/ℓ[i])=Φ[i-1], | |||
w(1) = W[i], | |||
subst([xi=1],diff(w(xi),xi)/ℓ[i])=Φ[i]]; | |||
/* solve for c's to comply with geometric boundary conditions */ | |||
coeffs : solve(bc, makelist(c[i],i,0,3))[1]; | |||
print("w(ξ) = ",facsum(expand(subst(coeffs,w(xi))),coords[1])); | |||
trialfcts: makelist(phi[i]=coeff(expand(subst(coeffs,w(xi))),coords[1][i]),i,1,4); | |||
plot2d(subst([ℓ[i]=5],subst(trialfcts,makelist(phi[i],i,1,4))), | |||
[xi,0,1],[xlabel,"ξ/1 →"], | |||
[legend,"φ1","5*φ2/ℓ","φ3","5*φ4/ℓ"]); | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
<!--------------------------------------------------------------------------------> | <!--------------------------------------------------------------------------------> | ||
{{MyCodeBlock|title=Equilibrium Conditions | {{MyCodeBlock|title=Equilibrium Conditions | ||
|text= | |text= | ||
So sind die Element-Steifigkeitsmatrix | |||
::<math>\displaystyle \underline{\underline{K}}_i=\,\frac{EI_i}{\ell_i^3}\begin{pmatrix}12 & 6\cdot {{\ell}_{i}} & -12 & 6\cdot {{\ell}_{i}}\\ 6\cdot {{\ell}_{i}} & 4\cdot {{\ell}_{i}^{2}} & -6\cdot {{\ell}_{i}} & 2\cdot {{\ell}_{i}^{2}}\\ -12 & -6\cdot {{\ell}_{i}} & 12 & -6\cdot {{\ell}_{i}}\\ 6\cdot {{\ell}_{i}} & 2\cdot {{\ell}_{i}^{2}} & -6\cdot {{\ell}_{i}} & 4\cdot {{\ell}_{i}^{2}}\end{pmatrix}</math> | |||
die Koordinaten des FE-Modells - hier für das Element "1": | |||
::<math>\underline{Q}\,=\,\begin{pmatrix}{{\Phi}_{0}}\\ {{W}_{1}}\\ {{\Phi}_{1}}\\ {{W}_{2}}\end{pmatrix}</math>. | |||
Wir komponieren daraus die System-Steifigkeitsmatrix - durch Aufaddieren der Beiträge der beiden Elemente und Einarbeiten der Randbedingugnen - zu | |||
::<math>\underline{\underline{K}}_0 =\begin{pmatrix} {K_A}+\frac{4 {{\mathit{EI}}_1}}{{\ell_1}} & -\frac{6 {{\mathit{EI}}_1}}{{{\ell}_{1}^{2}}} & \frac{2 {{\mathit{EI}}_1}}{{\ell_1}} & 0\\ -\frac{6 {{\mathit{EI}}_1}}{{{\ell}_{1}^{2}}} & {k_B}+\frac{12 {{\mathit{EI}}_2}}{{{\ell}_{2}^{3}}}+\frac{12 {{\mathit{EI}}_1}}{{{\ell}_{1}^{3}}} & \frac{6 {{\mathit{EI}}_2}}{{{\ell}_{2}^{2}}}-\frac{6 {{\mathit{EI}}_1}}{{{\ell}_{1}^{2}}} & -\frac{12 {{\mathit{EI}}_2}}{{{\ell}_{2}^{3}}}\\ \frac{2 {{\mathit{EI}}_1}}{{\ell_1}} & \frac{6 {{\mathit{EI}}_2}}{{{\ell}_{2}^{2}}}-\frac{6 {{\mathit{EI}}_1}}{{{\ell}_{1}^{2}}} & \frac{4 {{\mathit{EI}}_2}}{{\ell_2}}+\frac{4 {{\mathit{EI}}_1}}{{\ell_1}} & -\frac{6 {{\mathit{EI}}_2}}{{{\ell}_{2}^{2}}}\\ 0 & -\frac{12 {{\mathit{EI}}_2}}{{{\ell}_{2}^{3}}} & -\frac{6 {{\mathit{EI}}_2}}{{{\ell}_{2}^{2}}} & {k_C}+\frac{12 {{\mathit{EI}}_2}}{{{\ell}_{2}^{3}}}\end{pmatrix}</math> | |||
Wie das geht, steht in Abschnitt [[Randwertprobleme/Methoden zur Lösung von Randwertproblemen/Finite Elemente Methode|Finite Elemente Methode]]. | |||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
1+1 | /********************************************/ | ||
/* EUILIBRIUM CONDITIONS */ | |||
/* generic stiffness matrix */ | |||
K[i] : EI[i]/ℓ[i]^3*makelist(makelist( | |||
integrate( | |||
'diff(phi[i],xi,2)*'diff(phi[j],xi,2), | |||
xi,0,1), | |||
j,1,4),i,1,4); | |||
K[i] : subst(trialfcts,K[i]); | |||
K[i] : ev(K[i],nouns); | |||
K[i] : funmake('matrix,K[i]); | |||
/* compose system matrix */ | |||
NoN : 3; /* Number of Nodes*/ | |||
K[0] : zeromatrix(2*NoN,2*NoN); | |||
for m:1 thru 4 do | |||
for n:1 thru 4 do | |||
(K[0][ m, n] : K[0][ m, n] + subst([i=1],K[i][m,n]), | |||
K[0][2+m,2+n] : K[0][2+m,2+n] + subst([i=2],K[i][m,n])); | |||
/* add springs */ | |||
K[0][2,2] : K[0][2,2] + K[A]; /* Φ[0] */ | |||
K[0][3,3] : K[0][3,3] + K[B]; /* W[1] */ | |||
K[0][5,5] : K[0][5,5] + K[C]; /* W[2] */ | |||
Q : matrix([W[0]],[Φ[0]],[W[1]],[Φ[1]],[W[2]],[Φ[2]]); | |||
/* incorporate geometric boundary conditions */ | |||
/* eliminate rows / columns for W[0], Φ[2] (positions 1, 6) */ | |||
K[0] : submatrix(1,submatrix(6,K[0],6),1); | |||
Q : submatrix(1,submatrix(6,Q)); | |||
/* compose righ-hand-side */ | |||
P : transpose(funmake('matrix, | |||
[subst([i=1],append(makelist(integrate( | |||
ℓ[i]*subst(trialfcts,(q[A]*(1-xi)+q[B]*xi)*phi[j]), | |||
xi,0,1),j,1,4),[0,0]))] | |||
)); | |||
P[4,1] : P[4,1]+M[B]; | |||
/* eliminate BCs */ | |||
P : submatrix(1,6,P); | |||
print('K[i]," = ",EI[i]/ℓ[i]^3, ratsimp(K[i]/(EI[i]/ℓ[i]^3)))$ | |||
print('K[0]," = ", K[0])$ | |||
print("Q = ", Q)$ | |||
print("P = ", P)$ | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
<!--------------------------------------------------------------------------------> | <!--------------------------------------------------------------------------------> | ||
{{MyCodeBlock|title=Solving | {{MyCodeBlock|title=Solving | ||
|text= | |text= | ||
Die Knotenvariablen sind damit | |||
::<math>\begin{array}{ll}W_0 = 0& \\\Phi_0 = 0.00624& \\W_1 = 0.00657 m& \\\Phi_1 = 0.0123& \\W_2 = 0.00846 m& \\\Phi_2 = 0& \end{array}</math>. | |||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
1 | /********************************************/ | ||
/* SOLVE */ | |||
fpprintprec: 3; | |||
sol[1] : linsolve_by_lu(subst(params,K[0]),subst(params,P))[1]; | |||
sol[1] : append([W[0]=0],makelist(Q[i][1] = sol[1][i][1],i,1,4), [Φ[2]=0]); | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
<!--------------------------------------------------------> | |||
{{MyCodeBlock|title=Post-Processing | {{MyCodeBlock|title=Post-Processing | ||
|text= | |||
|text= | [[Datei:Kw96-21.png|mini|Biegelinie ''w(x)''|ohne]] | ||
Die Biegelinie des Balkens sieht damit so aus: | |||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
1+1 | /********************************************/ | ||
/* POSTPROCESS */ | |||
/* user parametric plot- hence t as independant variable */ | |||
f1 : subst([xi=t],subst(params,expand(subst(sol[1],subst([i=1],subst(coeffs,w(xi))))))); | |||
f2 : subst([xi=t],subst(params,expand(subst(sol[1],subst([i=2],subst(coeffs,w(xi))))))); | |||
scale : subst(params,(ℓ[2]/ℓ[1])); | |||
plot2d([[parametric, t, f1/m, [t, 0, 1]], | |||
[parametric, 1+t*scale, f2/m, [t, 0, 1]]], | |||
[gnuplot_preamble, "set yrange [] reverse"], | |||
[legend, "sec. I", "sec. II"], | |||
[xlabel, "x/ℓ[1] →"], | |||
[ylabel, "← w/m"])$ | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
<hr/> | <hr/> | ||
'''Links''' | '''Links''' | ||
* | * Analytische Lösung des Problems: [[Gelöste Aufgaben/Kw98|Kw98]] | ||
'''Literature''' | '''Literature''' | ||
* ... | * ... | ||
Aktuelle Version vom 31. März 2021, 13:48 Uhr
Aufgabenstellung
Ein Stab ABC ist durch eine lineare veränderliche Streckenlast q mit den Eckwerten qA in A und qB in B sowie dem Moment MB in B belastet. Der Stab (E-Modul: E) besteht aus zwei Sektionen mit den Längen l1 bzw. l2 sowie den Flächenmomenten I1 bzw. I2. Der Stab ist in A durch ein gelenkiges Festlager, in C durch eine Schiebehülse gelagert, in B sind die beiden Sektionen fest miteinander verbunden. Die Feder in A ist eine Drehfester mit Steifigkeit KA, die Federn in B und C sind Translationsfedern mit den Steifigkeiten kB, kC.
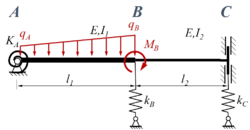
Gesucht ist die FEM Lösung für den Euler-Bernoulli-Balken unter Verwendung von zwei Finiten Elementen.
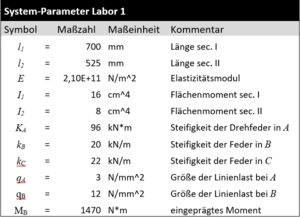
Ermitteln Sie für ein Euler-Bernoulli-Modell die analytischen Verläufe der Schnittgrößen und Verschiebungen im Balken für die angegebenen Parameter:
Die analytische Lösung finden Sie in Aufgabe Kw98.
Lösung mit Maxima
Header
Wir arbeiten mit den Standard-System-Matrizen nach Abschnitt "FEM-Formulierung für den Euler-Bernoulli-Balken".
/*******************************************************/
/* MAXIMA script */
/* version: wxMaxima 18.10.1 */
/* author: Andreas Baumgart */
/* last updated: 2019-02-10 */
/* ref: TM-C, Labor 4 */
/* description: finds the FE solution for */
/* lab problem #4 */
/*******************************************************/
Declarations
System-Parameter sind:
- .
/* declare variational variables - see 6.3 Identifiers */
declare("δA", alphabetic);
declare("δΠ", alphabetic);
declare("δW", alphabetic);
declare("δΦ", alphabetic);
declare("δw", alphabetic);
declare( "ℓ", alphabetic);
/* declarations */
assume(ℓ[i]>0);
/* system parameter */
units : [mm = m/1000, cm = m/100];
params : [q[A]=3*N/mm, ℓ[1]=700*mm, EI[1] = 2.1*10^11*N/m^2 * 3*cm*(4*cm)^3/12];
simple : [ℓ[2] = 3/4*ℓ[1], EI[2] = EI[1]/2,
K[A] = 2*EI[1]/ℓ[1], K[C] = 512/229*K[B]/2, K[B] = 2*EI[1]/ℓ[1]^3,
q[B] = 4*q[A], M[B] = q[A]*ℓ[1]^2];
params : append(params,makelist(
lhs(simple[i])=subst(params,rhs(simple[i])),i,1,length(simple)));
params : subst(units,params);
Formfunctions
Die Ansatzfunktion für die Trial-Functions ist ein Polynom 3. Grades:
An den Rändern müssen die Auslenkung und Kippung mit den Knoten-Variablen übereinstimmen:
- .
/**** define form functions ***/
/* coordinates */
coords : [[ W[i-1], Φ[i-1], W[i], Φ[i]],
[δW[i-1],δΦ[i-1],δW[i],δΦ[i]]];
/* generic polynomials */
define(w(xi),sum(c[i]*xi^(i),i,0,3));
/* … and boundary conditions */
bc : [w(0) = W[i-1],
subst([xi=0],diff(w(xi),xi)/ℓ[i])=Φ[i-1],
w(1) = W[i],
subst([xi=1],diff(w(xi),xi)/ℓ[i])=Φ[i]];
/* solve for c's to comply with geometric boundary conditions */
coeffs : solve(bc, makelist(c[i],i,0,3))[1];
print("w(ξ) = ",facsum(expand(subst(coeffs,w(xi))),coords[1]));
trialfcts: makelist(phi[i]=coeff(expand(subst(coeffs,w(xi))),coords[1][i]),i,1,4);
plot2d(subst([ℓ[i]=5],subst(trialfcts,makelist(phi[i],i,1,4))),
[xi,0,1],[xlabel,"ξ/1 →"],
[legend,"φ1","5*φ2/ℓ","φ3","5*φ4/ℓ"]);
Equilibrium Conditions
So sind die Element-Steifigkeitsmatrix
die Koordinaten des FE-Modells - hier für das Element "1":
- .
Wir komponieren daraus die System-Steifigkeitsmatrix - durch Aufaddieren der Beiträge der beiden Elemente und Einarbeiten der Randbedingugnen - zu
Wie das geht, steht in Abschnitt Finite Elemente Methode.
/********************************************/
/* EUILIBRIUM CONDITIONS */
/* generic stiffness matrix */
K[i] : EI[i]/ℓ[i]^3*makelist(makelist(
integrate(
'diff(phi[i],xi,2)*'diff(phi[j],xi,2),
xi,0,1),
j,1,4),i,1,4);
K[i] : subst(trialfcts,K[i]);
K[i] : ev(K[i],nouns);
K[i] : funmake('matrix,K[i]);
/* compose system matrix */
NoN : 3; /* Number of Nodes*/
K[0] : zeromatrix(2*NoN,2*NoN);
for m:1 thru 4 do
for n:1 thru 4 do
(K[0][ m, n] : K[0][ m, n] + subst([i=1],K[i][m,n]),
K[0][2+m,2+n] : K[0][2+m,2+n] + subst([i=2],K[i][m,n]));
/* add springs */
K[0][2,2] : K[0][2,2] + K[A]; /* Φ[0] */
K[0][3,3] : K[0][3,3] + K[B]; /* W[1] */
K[0][5,5] : K[0][5,5] + K[C]; /* W[2] */
Q : matrix([W[0]],[Φ[0]],[W[1]],[Φ[1]],[W[2]],[Φ[2]]);
/* incorporate geometric boundary conditions */
/* eliminate rows / columns for W[0], Φ[2] (positions 1, 6) */
K[0] : submatrix(1,submatrix(6,K[0],6),1);
Q : submatrix(1,submatrix(6,Q));
/* compose righ-hand-side */
P : transpose(funmake('matrix,
[subst([i=1],append(makelist(integrate(
ℓ[i]*subst(trialfcts,(q[A]*(1-xi)+q[B]*xi)*phi[j]),
xi,0,1),j,1,4),[0,0]))]
));
P[4,1] : P[4,1]+M[B];
/* eliminate BCs */
P : submatrix(1,6,P);
print('K[i]," = ",EI[i]/ℓ[i]^3, ratsimp(K[i]/(EI[i]/ℓ[i]^3)))$
print('K[0]," = ", K[0])$
print("Q = ", Q)$
print("P = ", P)$
Solving
Die Knotenvariablen sind damit
- .
/********************************************/
/* SOLVE */
fpprintprec: 3;
sol[1] : linsolve_by_lu(subst(params,K[0]),subst(params,P))[1];
sol[1] : append([W[0]=0],makelist(Q[i][1] = sol[1][i][1],i,1,4), [Φ[2]=0]);
Post-Processing
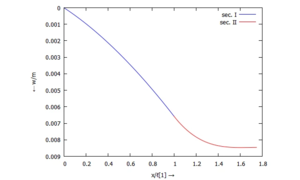
Die Biegelinie des Balkens sieht damit so aus:
/********************************************/
/* POSTPROCESS */
/* user parametric plot- hence t as independant variable */
f1 : subst([xi=t],subst(params,expand(subst(sol[1],subst([i=1],subst(coeffs,w(xi)))))));
f2 : subst([xi=t],subst(params,expand(subst(sol[1],subst([i=2],subst(coeffs,w(xi)))))));
scale : subst(params,(ℓ[2]/ℓ[1]));
plot2d([[parametric, t, f1/m, [t, 0, 1]],
[parametric, 1+t*scale, f2/m, [t, 0, 1]]],
[gnuplot_preamble, "set yrange [] reverse"],
[legend, "sec. I", "sec. II"],
[xlabel, "x/ℓ[1] →"],
[ylabel, "← w/m"])$
Links
- Analytische Lösung des Problems: Kw98
Literature
- ...