Gelöste Aufgaben/Kw56

Aufgabenstellung

Die Aufgabenstellung ist identisch mit Aufgabe Kw55, hier ist die Lösung mit dem Verfahren von Rayleigh-Ritz gefragt.

Lageplan

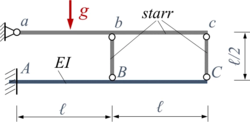
Gesucht ist eine Näherungslösung mit dem Verfahren von Rayleigh-Ritz für ein Euler-Bernoulli-Modell der Struktur.

Verwenden Sie zwei freie Trial-Funtions.

Lösung mit Maxima

Header

Die Herausforderung der Aufgabe liegt wieder in der kinematischen Zwangsbedingung, die der starre Stab abc dem Euler-Bernoulli-Balken auferlegt. Diese Zwangsbedingung lautet

$w_{B}=\displaystyle {\frac {1}{2}}w_{C}$,

mit den Abkürzungen

• w_B = w( ℓ),
• w_C = w(2ℓ).

Die geometrischen Randbedingungen in A erfüllen wir, indem wir Polynome ab dem Grad 2 verwenden.

Für die Lösung nach Rayleigh-Ritz können wir

• zwei freie Trial-Functions wählen, die die Zwangsbedingung selbst schon erfüllen
• mit Lagrange-Multiplikator die Zwangsbedingung einbauen.

Der zweite Weg ist bei Computer-Anwendungen meist viel einfacher - den gehen wir hier.

/*******************************************************/
/* MAXIMA script                                       */
/* version: wxMaxima 15.08.2                           */
/* author: Andreas Baumgart                            */
/* last updated: 2019-09-01                            */
/* ref: TMC                                            */
/* description: Rayley-Ritz-Solution for EBB           */
/*              with kinemtic constraints              */
/*******************************************************/

Declarations

Wir brauchen

$q_{0}=\displaystyle {\frac {m\,g}{\ell }}$

und nutzen eine Referenzlösung (wie in Kw55)

${\begin{array}{ccc}{\hat {w}}&=&\displaystyle {\frac {q_{0}\,(2\ell )^{4}}{8EI}}\\{\hat {\phi }}&=&\displaystyle {\frac {q_{0}\,(2\ell )^{3}}{6EI}}\end{array}}$.

/************************************************************/
/* declare variational variables - see 6.3 Identifiers      */
declare( "ℓ", alphabetic);
declare( "ϕ", alphabetic);
declare( "λ", alphabetic);

/* system parameters                                        */
params:  [q[0] = m*g/ℓ];
dimless: [ x   = xi*ℓ];

/* make equations of motion dim'less with load case #1 from Gross e.a., same as UEBI */
reference : [W[ref] = q[0]*(2*ℓ)^4/(8*EI), ϕ[ref] = q[0]*(2*ℓ)^3/(6*EI), M[ref] = m*g*ℓ, Q[ref] = 2*m*g];

Formfunctions

Um zwei freie Trial-Functions zu bekommen, müssen wir drei ansetzen: ein Freiheitsgrad wird von der kinematischen Zwangsbedingung aufgehoben.

Also wählen wir

$\displaystyle w(\xi )={\hat {w}}\cdot \sum _{i=2}^{4}W_{i}\cdot \xi ^{i}$

mit

$x=\xi \cdot \ell$

und ergänzen dies um die Zwangsbedingung

$2\cdot w(1)=\,w(2)$.

Achtung: Der Balken ist "2"-lang.

/************************************************************/
/* Rayleigh-Ritz                                            */
/* trial function */
trial: w(xi) = W[ref]*sum(W[j]*xi^(j),j,2,4);

/* kinemtic constraints                                     */
nodes : [W[B]=subst([xi=1], subst(trial,w(xi))), W[C]=subst([xi=2], subst(trial,w(xi)))];
BC: ratsimp(subst(nodes,[2*W[B]=W[C]])/W[ref])[1];

Equilibrium Conditions

Für die Gleichgewichtsbedingungen brauchen wir die potentielle Energie (hier die Lagrange-Funktion)

${\begin{array}{lcl}\Lambda =&&\displaystyle {\frac {1}{2\cdot \ell ^{3}}}\displaystyle EI\int _{0}^{2}\left(\displaystyle {\frac {d^{2}}{d\,\xi ^{2}}}\cdot w(\xi )\right)^{2}d\xi \\&-&\left(2m\,g+\displaystyle {\frac {1}{2}}m\,g\right)\cdot w(1)+\left(\displaystyle {\frac {1}{2}}m\,g\right)\cdot w(2)\\&+&\lambda \cdot \displaystyle {\frac {m^{2}\,g^{2}\ell ^{3}}{EI}}\cdot (2\,w(1)-w(2))\end{array}}$

wobei der konstante Faktor bei dem Lagrange-Multiplikator λ nur der Ästhetik dient ....

Die gesuchten Größen sind nun

${\underline {Q}}=\left({\begin{array}{c}W_{2}\\W_{3}\\W_{4}\\\lambda \end{array}}\right)$,

und die Gleichgewichtsbedingungen kommen aus

$\displaystyle {\frac {d\Lambda }{dQ_{i}}}{\stackrel {!}{=}}0$

zu

${\begin{array}{cc}-2\lambda +256{W_{4}}+96{W_{3}}+32{W_{2}}-1&=0,\\-2\lambda +384{W_{4}}+128{W_{3}}+32{W_{2}}+1&=0,\\70\lambda -18432{W_{4}}-5760{W_{3}}-1280{W_{2}}-55&=0,\\-7{W_{4}}-3{W_{3}}-{W_{2}}&=0\end{array}}$.

/* Lagrange formulation */
Lambda : + 1/2*ℓ*'integrate(EI*diff(w(xi),xi,2)^2/ℓ^4,xi,0,2)
         - (2*m*g+m*g/2)*subst(nodes, W[B])+(m*g/2)*subst(nodes,W[C])
         + λ*m*g*(lhs(BC)-rhs(BC));
Lambda : subst(trial,Lambda);
Lambda : ev(Lambda, nouns);

X : append(makelist(W[j],j,2,4),[λ]);

fact: g^2*m^2*ℓ^3/EI; 
eom : ratsimp(subst(params,subst(reference,
       makelist(diff(Lambda/fact,X[i])=0,i,1,length(X))
      )));

Solving

Dieses lineare Gleichungssystem hat die Lösung

$\displaystyle {{W}_{2}}={\frac {23}{56}},{{W}_{3}}=-{\frac {27}{112}},{{W}_{4}}={\frac {5}{112}},\lambda ={\frac {3}{14}}$

/* solve! */
sol: solve(eom,X)[1];

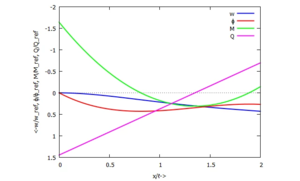
Post-Processing

Einsetzen in die Trial-Functions liefert die (dimensionslosen) Funktionsverläufe für w, ϕ, M und Q:

Verläufe der gesuchten Größen

/************************************************************/
/* post - processing                                        */

/* cross-sectional bending moment */

toPlot : [
           w[xi] = ratsimp(subst(trial,w(xi))/W[ref]),
           ϕ[xi] = ratsimp(subst(params,subst(reference,    diff(subst(trial,w(xi)),xi,1)/ℓ^1/ϕ[ref]))),
           M[xi] = ratsimp(subst(params,subst(reference,-EI*diff(subst(trial,w(xi)),xi,2)/ℓ^2/M[ref]))),
           Q[xi] = ratsimp(subst(params,subst(reference,-EI*diff(subst(trial,w(xi)),xi,3)/ℓ^3/Q[ref])))
          ];

plot2d(subst(sol,subst(toPlot,[w[xi],ϕ[xi],M[xi],Q[xi]])),[xi,0,1],
       [gnuplot_preamble, "set yrange [] reverse"],
       [legend, "w", "ϕ", "M", "Q"],
       [xlabel, "x/ℓ->"], [ylabel, "<-w/w_ref, ϕ/ϕ_ref, M/M_ref, Q/Q_ref"],
       [style, [lines,2]]);

---

Links

• ...

Literature

• ...