Anfangswertprobleme/Methoden zur Lösung von Anfangswertproblemen/Euler-Streckenzug-Verfahren: Unterschied zwischen den Versionen
Die Seite wurde neu angelegt: „x“ |
Keine Bearbeitungszusammenfassung |
||
| (Eine dazwischenliegende Version desselben Benutzers wird nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
Beim Euler-Streckenzug- oder Euler-Einschritt-Verfahren wiederholt man für die numerische Lösung des Anfangswertproblems | |||
::<math>\underline{\dot{q}}(t) = \underline{f}(\underline{q}(t),t)</math> | |||
konsequent den Schritt | |||
::<math>\underline{q}_{i+1} = \underline{q}_i + \underline{\dot{q}}|_{t=t_i}\cdot\Delta t \text{ mit } \underline{\dot{q}}|_{t=t_i} = \underline{f}(\underline{q}_i,t_i)</math> | |||
In dieser Gleichung steckt der Differenzenquotient | |||
::<math>\displaystyle \dot{q}_{t_i} \approx \frac{q(t_i+\Delta t) - q(t_i)}{\Delta t}</math> | |||
den wir nach ''q(t+Δt)'' auflösen. | |||
So sehen die ersten beiden Schritte für das Einführungs-[[Anfangswertprobleme/Methoden zur Lösung von Anfangswertproblemen|Beispiel]] so aus: | |||
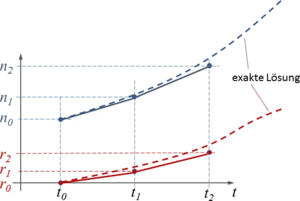
[[Datei:Euler-Verfahren-Integrationschritt.png|ohne|mini|Analytische und numerische Näherungslösung]] | |||
Jeder dieser Schritte ist für sich trivial, erfordert aber die Durchführung von sehr vielen Rechenoperationen. Mit den ersten Computern hat dieses Verfahren deshalb seine große Bedeutung bekommen. | |||
Die Umsetzung dieses Verfahrens ist konzeptionell wichtig, weil es das Vorgehen zur numerischen Lösung von Anfangswerten verdeutlicht. Für die praktische Umsetzung ist es in dieser Form nicht empfehlenswert, da es ungenau und numerisch ineffizient ist. | |||
Allerdings gehen alle praktikablen Lösungsverfahren aus die Grundidee dieses Verfahrens zurück: | |||
* addiere sukzessive kleine Inkremente zu der Zustandsgrößen des Ausgangs-Zustands, indem die Werte der Ableitungen (Rechte Seite der Gleichung) mit kleinen Zeitschritten hinzugefügt werden. | |||
Aktuelle Version vom 22. Februar 2021, 12:14 Uhr
Beim Euler-Streckenzug- oder Euler-Einschritt-Verfahren wiederholt man für die numerische Lösung des Anfangswertproblems
konsequent den Schritt
In dieser Gleichung steckt der Differenzenquotient
den wir nach q(t+Δt) auflösen.
So sehen die ersten beiden Schritte für das Einführungs-Beispiel so aus:
Jeder dieser Schritte ist für sich trivial, erfordert aber die Durchführung von sehr vielen Rechenoperationen. Mit den ersten Computern hat dieses Verfahren deshalb seine große Bedeutung bekommen.
Die Umsetzung dieses Verfahrens ist konzeptionell wichtig, weil es das Vorgehen zur numerischen Lösung von Anfangswerten verdeutlicht. Für die praktische Umsetzung ist es in dieser Form nicht empfehlenswert, da es ungenau und numerisch ineffizient ist.
Allerdings gehen alle praktikablen Lösungsverfahren aus die Grundidee dieses Verfahrens zurück:
- addiere sukzessive kleine Inkremente zu der Zustandsgrößen des Ausgangs-Zustands, indem die Werte der Ableitungen (Rechte Seite der Gleichung) mit kleinen Zeitschritten hinzugefügt werden.