Gelöste Aufgaben/W8Zu: Unterschied zwischen den Versionen
Die Seite wurde neu angelegt: „g“ |
Keine Bearbeitungszusammenfassung |
||
| (5 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
[[Category:Gelöste Aufgaben]] | |||
[[Category:Numerische Lösung]] | |||
[[Category:Randwertproblem]] | |||
[[Category:Prinzip vom Minimum der Potentiellen Energie]] | |||
[[Category:Biege-Belastung]][[Category:Euler-Bernoulli-Balken]] | |||
[[Category:Rayleigh-Ritz-Prinzip]] | |||
[[Category:Maxima]] | |||
==Aufgabenstellung== | |||
Zu den tabellierten [[Sources/Lexikon/Euler-Bernoulli-Balken/Standard-Lösungen#Einzellast, doppeltgelenkige Lagerung|Standardlösungen für den Euler-Bernoulli-Blaken]] berechnen wir eine Näherungslösung für einen beidseitig gelenkig gelagerten Euler-Bernoulli-Balken: | |||
<onlyinclude> | |||
[[Datei:W8Zt-01.png|250px|left|mini|Caption]] | |||
Gesucht ist eine Lösung in Anlehnung an das Verfahren von Ryleigh-Ritz. | |||
</onlyinclude> | |||
Die Lösung nach einer Variante zu diesem Standardverfahren finden Sie hier in [[Gelöste Aufgaben/W8Zt|W8Zt]]. | |||
== Lösung mit Maxima == | |||
Mit dem [[Sources/Lexikon/Föppl-Symbol|Föppl-Symbol "<>"]], sowie | |||
::<math>\alpha = a/\ell</math>, <math>\beta = 1-\alpha</math> und <math>\xi = x/\ell</math> | |||
ist die analytische Lösung: | |||
::<math>EI w(x) = \frac{\displaystyle F \ell^3}{\displaystyle 6}\left[ \beta \xi ( 1-\beta^2-\xi^2)+<\xi-\alpha>^3 \right]</math>. | |||
Bei dieser Lösung hat die [[Sources/Lexikon/unabhängige Koordinaten|unabhängige Koordinate]] ''x'' ihren Ursprung in ''A'' - wir verwenden unten einen anderen Ursprung! | |||
Mit den passenden Ansatzfunktionen nach Ritz berechnen Sie eine Näherungslösung des Problems nach dem [[Werkzeuge/Gleichgewichtsbedingungen/Arbeitsprinzipe der Analytischen Mechanik/Prinzip vom Minimum der Potentiellen Energie|Prinzip vom Minimum der Potentiellen Energie]]. | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Header | |||
|text=Wir lösen das Problem mit [[Werkzeuge/Software/Maxima|Maxima]]. | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
/*******************************************************/ | |||
/* MAXIMA script */ | |||
/* version: wxMaxima 15.08.2 */ | |||
/* author: Andreas Baumgart */ | |||
/* last updated: 2017-10-14 */ | |||
/* ref: TM-C, Labor 3 - aus Gross, Augf. TM 2, Biegetab*/ | |||
/* description: finds the approx. solution for */ | |||
/* problem #1 using PMPE */ | |||
/*******************************************************/ | |||
</syntaxhighlight> | |||
}} | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Declarations | |||
|text= | |||
In Maxima treffen wir die Annahme ℓ>0, damit einige Integrale richtig gelöst werden. | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
/* declarations */ | |||
assume(l>0); | |||
</syntaxhighlight> | |||
}} | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Formfunctions | |||
|text= | |||
Als [[Sources/Lexikon/unabhängige Koordinaten|unabhängige Koordinaten]] des Balkens wählen wir "''x''" entlang der [[Sources/Lexikon/Euler-Bernoulli-Balken/Neutrale Faser|Neutralen Faser]] mit Ursprung in der Mitte zwischen A und B. | |||
Wir entscheiden uns zunächst für zwei abhängige Koordinaten des Systems | |||
::<math>\underline{q} = \left(\begin{array}{c}V\\\Psi \end{array}\right)</math> | |||
[[Datei:W8Zt-11.png|mini|200x200px|Trial-Functions]] | |||
und wählen ''V'' und ψ als die Verschiebung und Verdrehung (=Neigung) des Querschnitts im Punkt ''x''=0 des Balkens. | |||
Jetzt brauchen wir zwei [[Sources/Lexikon/Ansatzfunktion|Ansatzfunktionen]], die unseren Koordinaten ''V'' und ''ψ'' entsprechen. Wir wollen diese beiden anschaulich denken können - wir wählen einfache Polynome: eine achsensymmetrische und eine punktsymmetrische Funktion mit den noch unbestimmten Konstanten ''c<sub>ij</sub>'': | |||
* <math>{{v}_{1}}\left( x\right) :={{c}_{1,2}}\cdot {{x}^{2}}+{{c}_{1,0}}</math> | |||
* <math>v_{2} (x) := c_{2,3} \cdot x^3+c_{2,1} \cdot x</math> | |||
Diese beiden Funktionen müssen | |||
# [[Sources/Lexikon/Geometrische Randbedingungen|Geometrische Randbedingungen]] erfüllen und | |||
# jeweils mit den Koordinaten ''V'' und ''ψ'' verknüpft werden. | |||
Die zugehörigen Gleichungen (= die Randbedingungen) sind | |||
* <math>{{c}_{1,0}}=V,\;\;\;\frac{\displaystyle {{c}_{1,2}}\cdot {{\ell}^{2}}}{\displaystyle 4}+{{c}_{1,0}}=0</math> und | |||
* <math>{{c}_{2,1}}=\Psi,\;\;\;\frac{\displaystyle {{c}_{2,3}}\cdot {{\ell}^{3}}}{\displaystyle 8}+\frac{\displaystyle {{c}_{2,1}}\cdot \ell}{\displaystyle 2}=0</math> | |||
mit der Lösung | |||
::<math>\begin{array}{l} | |||
{{c}_{1,0}}=V,\\ | |||
{{c}_{1,2}}=-\frac{\displaystyle 4\cdot V}{{{\displaystyle \ell}^{2}}},\\ | |||
{{c}_{2,1}}=\Psi,\\ | |||
{{c}_{2,3}}=-\frac{\displaystyle 4\cdot \Psi}{\displaystyle {{\ell}^{2}}} | |||
\end{array}</math> | |||
Anstatt der exakten, bekannten Lösung, verwenden wir in diesem Näherungsansatz also nun die Funktion | |||
::<math>w\left( x\right) =-\frac{\displaystyle 4\cdot {{x}^{2}}\cdot V}{{\displaystyle {\ell}^{2}}}+V-\frac{\displaystyle 4\cdot \Psi\cdot {{x}^{3}}}{{\displaystyle {\ell}^{2}}}+\Psi\cdot x</math>, | |||
mit den beiden Koordinaten ''V'' und ''ψ''. die wir nun bestimmen müssen. Anschaulich können wir nun | |||
::<math>w(\xi) = V\cdot \phi_1(\xi) + \Phi\cdot \phi_2(\xi)</math> | |||
mit | |||
::<math>\begin{array}{ll}\phi_1(\xi) &= 1-4\cdot {{\xi}^{2}}\\\phi_2(\xi) &= \ell\cdot \xi-4\cdot \ell\cdot {{\xi}^{3}}\end{array}</math> | |||
[[Datei:W8Zt-12.png|mini|Trial-Functions ''ϕ<sub>1</sub>'', ''ϕ<sub>2</sub>'']] | |||
schreiben. So sehen die beiden Trial-Funktionen aus: | |||
Klar ist: die exakte Lösung dieses Lastfalls ist eine Funktion, die im [[Sources/Lexikon/Querkraftverlauf|Querkraftverlauf]] am Kraftangriffspunkt (''x=a - ℓ/2'') einen Sprung hat. Dagegen ist der Querkraftverlauf unserer Näherungslösung stetig differenzierbar und obendrauf noch konstant! | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
/**** define form functions ***/ | |||
/* coordinates */ | |||
q : [V,Psi]; | |||
/* generic polynomials */ | |||
define(v[1](x),sum(c[1,2*i]*x^(2*i),i,0,1)); | |||
define(v[2](x),sum(c[2,(2*i+1)]*x^(2*i+1),i,0,1)); | |||
/* solve for c's to comply with geometric boundary conditions */ | |||
coeffs : append(solve([v[1](0)=V,v[1](+l/2)=0],[c[1,0],c[1,2]])[1], | |||
solve([subst([x=0],diff(v[2](x),x))=Psi,v[2](+l/2)=0],[c[2,1],c[2,3]])[1]); | |||
/* employ in polynomials */ | |||
forms : [w(x) = expand(subst(coeffs, sum(v[i](x),i,1,2)))]; | |||
trials: subst([x=l*xi],makelist(coeff(subst(forms,w(x)), q[i]),i,1,2)); | |||
plot2d( [trials[1],trials[2]/l],[xi,-1/2,+1/2], [legend, "ϕ[1]","ϕ[2]"]); | |||
</syntaxhighlight> | |||
}} | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Equilibrium Conditions | |||
|text= | |||
Mit dem [[Werkzeuge/Gleichgewichtsbedingungen/Arbeitsprinzipe der Analytischen Mechanik/Prinzip vom Minimum der Potentiellen Energie|Prinzip vom Minimum der Potentiellen Energie]] sind die Gleichgewichtsbedingungen | |||
::<math>\displaystyle \frac{\partial U}{\partial q_i}\stackrel{!}{=}0 \text{ für alle Koordinaten }i.</math>, | |||
dabei ist | |||
::<math>U = \Pi - A, \;\; \text{ mit } \Pi \text{: elastisches Potential und } A \text{: Arbeit der Kraft F.}</math>. | |||
Einsetzen der Trial-Funktionen liefert | |||
::<math>\begin{array}{l}\displaystyle A=F\cdot \left( -{{\alpha}^{2}}\cdot V+V-\frac{{{\alpha}^{3}}\cdot \ell\cdot \Psi}{2}+\frac{\alpha\cdot \ell\cdot \Psi}{2}\right) \\\displaystyle \Pi=\mathit{EI}\cdot \int_{-\frac{\ell}{2}}^{\frac{\ell}{2}}{{\left( \frac{{{d}^{2}}}{d\,{{x}^{2}}}\cdot \left( \Psi\cdot x-\frac{4\cdot \Psi\cdot {{x}^{3}}}{{{\ell}^{2}}}+V-\frac{4\cdot {{x}^{2}}\cdot V}{{{\ell}^{2}}}\right) \right) }^{2}}dx\end{array}</math> | |||
und wir finden nach dem Ausführen der Differentiation und Integration | |||
::<math>\displaystyle U=-\frac{64\cdot \mathit{EI}\cdot {{V}^{2}}}{{{\ell}^{3}}}-{{\alpha}^{2}}\cdot F\cdot V+F\cdot V-\frac{{{\alpha}^{3}}\cdot \ell\cdot \Psi\cdot F}{2}+\frac{\alpha\cdot \ell\cdot \Psi\cdot F}{2}-\frac{48\cdot {{\Psi}^{2}}\cdot \mathit{EI}}{\ell}</math> | |||
Achtung: hier bezeichnet nun ''α=-1'' den Punkt A, ''α=+1'' den Punkt B. | |||
Die Koordinaten fassen wir zu | |||
::<math>\underline{q} = \left( \begin{array}{c} V\\ \Psi\end{array}\right)</math> | |||
zusammen und schreiben damit | |||
::<math>\displaystyle U(\underline{q}) = \frac{1}{2} \; \underline{q}^T\cdot \underline{\underline{A}}\cdot \underline{q} - \underline{q}^T \cdot \underline{b}</math> | |||
mit | |||
::<math>\underline{\underline{A}} = \begin{pmatrix}\displaystyle -\frac{64\cdot \mathit{EI}}{{{\ell}^{3}}} & 0\\ 0 & \displaystyle -\frac{48\cdot \mathit{EI}}{\ell}\end{pmatrix}</math> | |||
und | |||
::<math>\underline{b} = \begin{pmatrix}{{\alpha}^{2}}\cdot F-F\\ \displaystyle \frac{{{\alpha}^{3}}\cdot \ell\cdot F}{2}-\frac{\alpha\cdot \ell\cdot F}{2}\end{pmatrix}</math> | |||
Mit dieser Formulierung sind wir bei den [[Sources/Lexikon/Minimum Prinzipe|Minimum Prinzipen]] angekommen, die Lösung kommt aus dem linearen Gleichungssystem | |||
::<math>\underline{\underline{A}}\cdot\underline{q} = \underline{b}</math> | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
/* potential energy of system */ | |||
PMPE : U = A-Pi; | |||
parts : [/*virt. strain energy */ | |||
A = F*w(x[F]), | |||
/* work of implied external force F*/ | |||
Pi = integrate(EI*diff(w(x),x,2)^2,x,-l/2,+l/2)]; | |||
parts : subst([w(x[F]) = subst([x=\alpha*l/2], subst(forms,w(x)))],parts); | |||
parts : subst(forms,parts); | |||
/* substitute .... */ | |||
PMPE : subst(forms,subst(parts,PMPE)); | |||
/* execute differntiation and integration of δW */ | |||
PMPE : expand(ev(PMPE,nouns)); | |||
/* pick individual equations */ | |||
OLE: [b = - makelist([coeff(subst(PMPE,U),q[i])],i,1,2), | |||
A = [[coeff(subst(PMPE,U),q[1],2),0],[0,coeff(subst(PMPE,U),q[2],2)]]]; | |||
</syntaxhighlight> | |||
}} | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Solve | |||
|text= | |||
Die Lösung für die Koordinaten ''<u>q</u>'' ist | |||
::<math>\begin{array}{l}V=\displaystyle -\frac{\left( {{\alpha}^{2}}-1\right) \cdot {{\ell}^{3}}\cdot F}{64\cdot \mathit{EI}}\\ | |||
\Psi=\displaystyle -\frac{\left( {{\alpha}^{3}}-\alpha\right) \cdot {{\ell}^{2}}\cdot F}{96\cdot \mathit{EI}}\end{array}</math> | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
/* solve .... */ | |||
K: funmake('matrix,subst(OLE,A)); | |||
f : funmake('matrix,subst(OLE,b)); | |||
print(K,transpose(q)=f)$ | |||
equs : makelist((K.q)[i][1]=f[i][1],i,1,2); | |||
sol: solve(equs,q)[1]; | |||
</syntaxhighlight> | |||
}} | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Post-Process | |||
|text= | |||
Die Lösung normieren wir noch für das Post-Processing mit der analytischen maximalen Auslenkung im symmetrischen Belastungsfall (wenn ''F'' in der Mitte zwischen A und B angreift): | |||
Wir tragen sie für verschiedene Kraft-Angriffspunkte (''α=-1,...α=+1'') auf: | |||
[[Datei:W8Zt-31.png|ohne|mini|Auslenkung ''w(x)'' am Kraftangriffspunkt]] | |||
{{MyAttention|title=Wissen Sie ...|text=... warum A hier eine Diagonalmatrix ist? Schauen Sie sich die Formel zur Berechnung der Koeffizienten ''a<sub>ij</sub>'' an - was erkennen Sie?}} | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
/* plot results */ | |||
m : 2; scale : F*l^3/(EI*48); | |||
leg : append([legend],makelist(simplode(["α=",(-m+i)/m]),i,0,2*m)); | |||
plotfct : expand(subst([x=xi*l],subst(sol,subst(forms,w(x)/scale)))); | |||
toplot : makelist(subst([alpha=(-m+i)/m],plotfct),i,0,2*m); | |||
plot2d(subst([alpha=0],toplot),[xi,-1/2,+1/2], [y,-0.05,1.0], leg); | |||
</syntaxhighlight> | |||
}} | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Post-Process: Compare with Analytic Solution | |||
|text= | |||
Und wir schauen uns für ''α=1/2'' die Verschiebung der Ritz- und analytischen-Lösung im Vergleich an: | |||
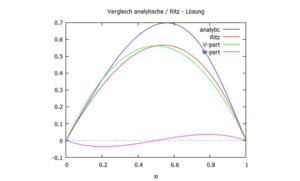
[[Datei:W8Zt-32.png|ohne|mini|Vergleich von analytischer / numerischer Lösung für ''w(x)'']] | |||
{{MyTip|title=Und wissen Sie auch ...|text=... wie der Verlauf der Querkraft im Vergleich Ritz / analytisch aussieht?}} | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
/* Vergleich mit analytischer Lösung */ | |||
foppl(xi,alpha) := if (xi < alpha) then 0 else xi-alpha; | |||
anplot : F*l^3/(6*EI)*(beta*xi*(1-beta^2-xi^2)+foppl(xi,alpha)^3)/scale; | |||
anplot : subst([beta=1-alpha],anplot); | |||
ritz: subst([xi=xi-1/2],subst(alpha=1/2,expand(subst(sol,makelist(trials[i]*q[i]/scale,i,1,2))))); | |||
plot2d([subst([alpha=3/4],anplot),ritz[1]+ritz[2], ritz[1],ritz[2]],[xi,0,1], | |||
[legend, "analytic", "Ritz", "V-part", "Ψ-part"], | |||
[title, "Vergleich analytytische / Ritz - Lösung"]) | |||
</syntaxhighlight> | |||
}} | |||
<hr/> | |||
'''Links''' | |||
* ... | |||
'''Literature''' | |||
* ... | |||
Aktuelle Version vom 19. April 2021, 11:09 Uhr
Aufgabenstellung
Zu den tabellierten Standardlösungen für den Euler-Bernoulli-Blaken berechnen wir eine Näherungslösung für einen beidseitig gelenkig gelagerten Euler-Bernoulli-Balken:
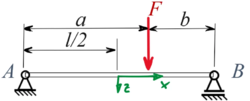
Gesucht ist eine Lösung in Anlehnung an das Verfahren von Ryleigh-Ritz.
Die Lösung nach einer Variante zu diesem Standardverfahren finden Sie hier in W8Zt.
Lösung mit Maxima
Mit dem Föppl-Symbol "<>", sowie
- , und
ist die analytische Lösung:
- .
Bei dieser Lösung hat die unabhängige Koordinate x ihren Ursprung in A - wir verwenden unten einen anderen Ursprung!
Mit den passenden Ansatzfunktionen nach Ritz berechnen Sie eine Näherungslösung des Problems nach dem Prinzip vom Minimum der Potentiellen Energie.
Header
Wir lösen das Problem mit Maxima.
/*******************************************************/
/* MAXIMA script */
/* version: wxMaxima 15.08.2 */
/* author: Andreas Baumgart */
/* last updated: 2017-10-14 */
/* ref: TM-C, Labor 3 - aus Gross, Augf. TM 2, Biegetab*/
/* description: finds the approx. solution for */
/* problem #1 using PMPE */
/*******************************************************/
Declarations
In Maxima treffen wir die Annahme ℓ>0, damit einige Integrale richtig gelöst werden.
/* declarations */
assume(l>0);
Formfunctions
Als unabhängige Koordinaten des Balkens wählen wir "x" entlang der Neutralen Faser mit Ursprung in der Mitte zwischen A und B.
Wir entscheiden uns zunächst für zwei abhängige Koordinaten des Systems
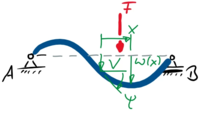
und wählen V und ψ als die Verschiebung und Verdrehung (=Neigung) des Querschnitts im Punkt x=0 des Balkens.
Jetzt brauchen wir zwei Ansatzfunktionen, die unseren Koordinaten V und ψ entsprechen. Wir wollen diese beiden anschaulich denken können - wir wählen einfache Polynome: eine achsensymmetrische und eine punktsymmetrische Funktion mit den noch unbestimmten Konstanten cij:
Diese beiden Funktionen müssen
- Geometrische Randbedingungen erfüllen und
- jeweils mit den Koordinaten V und ψ verknüpft werden.
Die zugehörigen Gleichungen (= die Randbedingungen) sind
- und
mit der Lösung
Anstatt der exakten, bekannten Lösung, verwenden wir in diesem Näherungsansatz also nun die Funktion
- ,
mit den beiden Koordinaten V und ψ. die wir nun bestimmen müssen. Anschaulich können wir nun
mit
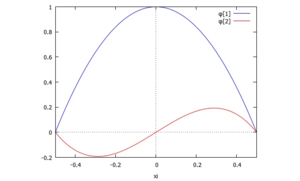
schreiben. So sehen die beiden Trial-Funktionen aus:
Klar ist: die exakte Lösung dieses Lastfalls ist eine Funktion, die im Querkraftverlauf am Kraftangriffspunkt (x=a - ℓ/2) einen Sprung hat. Dagegen ist der Querkraftverlauf unserer Näherungslösung stetig differenzierbar und obendrauf noch konstant!
/**** define form functions ***/
/* coordinates */
q : [V,Psi];
/* generic polynomials */
define(v[1](x),sum(c[1,2*i]*x^(2*i),i,0,1));
define(v[2](x),sum(c[2,(2*i+1)]*x^(2*i+1),i,0,1));
/* solve for c's to comply with geometric boundary conditions */
coeffs : append(solve([v[1](0)=V,v[1](+l/2)=0],[c[1,0],c[1,2]])[1],
solve([subst([x=0],diff(v[2](x),x))=Psi,v[2](+l/2)=0],[c[2,1],c[2,3]])[1]);
/* employ in polynomials */
forms : [w(x) = expand(subst(coeffs, sum(v[i](x),i,1,2)))];
trials: subst([x=l*xi],makelist(coeff(subst(forms,w(x)), q[i]),i,1,2));
plot2d( [trials[1],trials[2]/l],[xi,-1/2,+1/2], [legend, "ϕ[1]","ϕ[2]"]);
Equilibrium Conditions
Mit dem Prinzip vom Minimum der Potentiellen Energie sind die Gleichgewichtsbedingungen
- ,
dabei ist
- .
Einsetzen der Trial-Funktionen liefert
und wir finden nach dem Ausführen der Differentiation und Integration
Achtung: hier bezeichnet nun α=-1 den Punkt A, α=+1 den Punkt B.
Die Koordinaten fassen wir zu
zusammen und schreiben damit
mit
und
Mit dieser Formulierung sind wir bei den Minimum Prinzipen angekommen, die Lösung kommt aus dem linearen Gleichungssystem
/* potential energy of system */
PMPE : U = A-Pi;
parts : [/*virt. strain energy */
A = F*w(x[F]),
/* work of implied external force F*/
Pi = integrate(EI*diff(w(x),x,2)^2,x,-l/2,+l/2)];
parts : subst([w(x[F]) = subst([x=\alpha*l/2], subst(forms,w(x)))],parts);
parts : subst(forms,parts);
/* substitute .... */
PMPE : subst(forms,subst(parts,PMPE));
/* execute differntiation and integration of δW */
PMPE : expand(ev(PMPE,nouns));
/* pick individual equations */
OLE: [b = - makelist([coeff(subst(PMPE,U),q[i])],i,1,2),
A = [[coeff(subst(PMPE,U),q[1],2),0],[0,coeff(subst(PMPE,U),q[2],2)]]];
Solve
Die Lösung für die Koordinaten q ist
/* solve .... */
K: funmake('matrix,subst(OLE,A));
f : funmake('matrix,subst(OLE,b));
print(K,transpose(q)=f)$
equs : makelist((K.q)[i][1]=f[i][1],i,1,2);
sol: solve(equs,q)[1];
Post-Process
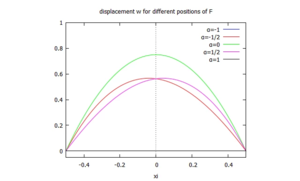
Die Lösung normieren wir noch für das Post-Processing mit der analytischen maximalen Auslenkung im symmetrischen Belastungsfall (wenn F in der Mitte zwischen A und B angreift):
Wir tragen sie für verschiedene Kraft-Angriffspunkte (α=-1,...α=+1) auf:
| ⚠ Wissen Sie ...: |
| ... warum A hier eine Diagonalmatrix ist? Schauen Sie sich die Formel zur Berechnung der Koeffizienten aij an - was erkennen Sie? |
/* plot results */
m : 2; scale : F*l^3/(EI*48);
leg : append([legend],makelist(simplode(["α=",(-m+i)/m]),i,0,2*m));
plotfct : expand(subst([x=xi*l],subst(sol,subst(forms,w(x)/scale))));
toplot : makelist(subst([alpha=(-m+i)/m],plotfct),i,0,2*m);
plot2d(subst([alpha=0],toplot),[xi,-1/2,+1/2], [y,-0.05,1.0], leg);
Post-Process: Compare with Analytic Solution
Und wir schauen uns für α=1/2 die Verschiebung der Ritz- und analytischen-Lösung im Vergleich an:
| ✔ Und wissen Sie auch ...: |
| ... wie der Verlauf der Querkraft im Vergleich Ritz / analytisch aussieht? |
/* Vergleich mit analytischer Lösung */
foppl(xi,alpha) := if (xi < alpha) then 0 else xi-alpha;
anplot : F*l^3/(6*EI)*(beta*xi*(1-beta^2-xi^2)+foppl(xi,alpha)^3)/scale;
anplot : subst([beta=1-alpha],anplot);
ritz: subst([xi=xi-1/2],subst(alpha=1/2,expand(subst(sol,makelist(trials[i]*q[i]/scale,i,1,2)))));
plot2d([subst([alpha=3/4],anplot),ritz[1]+ritz[2], ritz[1],ritz[2]],[xi,0,1],
[legend, "analytic", "Ritz", "V-part", "Ψ-part"],
[title, "Vergleich analytytische / Ritz - Lösung"])
Links
- ...
Literature
- ...