Gelöste Aufgaben/Kv53: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| (11 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 11: | Zeile 11: | ||
==Aufgabenstellung== | ==Aufgabenstellung== | ||
Eine Kiste der Masse ''m'' bewegt sich auf einer schiefen Ebene, die unter dem Winkel ''α'' gegenüber der Horizontalen geneigt ist. Zwischen Kiste und Ebene wirkt eine Reibkraft (Haft-Koeffizient ''μ<sub>0</sub>'', Reib-Koeffizient ''μ<sub>1</sub>''). Zu Beginn der Bewegung wird die Kiste wie skizziert um den Betrag ''Δℓ'' in eine Feder der Steifigkeit ''k'' eingedrückt und dann losgelassen. | |||
<onlyinclude> | <onlyinclude> | ||
[[Datei: | [[Datei:Kv53-01.png|alternativtext=|links|mini|250x250px|Lageplan]] | ||
Gesucht ist | Gesucht ist die nichtlineare Bewegungsgleichung mit Reibkennlinie sowie die numerische Lösung als Anfangswertproblem. | ||
</onlyinclude> | </onlyinclude> | ||
Dabei sollen verschiedene Ergebnis-Muster gezeigt werden: | |||
# die Kiste bleibt nach der ersten Aufwärts-Bewegung auf der Ebene bei ''B'' haften und bewegt sich nicht weiter. | |||
# die Kiste erfährt mehrere Aufwärts- und Abwärts-Bewegungen, bevor sie liegen bleibt. | |||
== Lösung mit Maxima == | == Lösung mit Maxima == | ||
<!--------------------------------------------------------------------------------> | <!--------------------------------------------------------------------------------> | ||
{{MyCodeBlock|title=Header | {{MyCodeBlock|title=Header | ||
|text= | |text= | ||
Wir stellen die Bewegungsgleichungen des Systems als System con Differentialgleichungen erster Ordnung auf. Die Nichtlinearität kommt aus der Reibkraft und dem "Abheben" der Kiste von der Feder. | |||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
/*********************************************************/ | |||
/* MAXIMA script */ | |||
/* version: wxMaxima 15.08.2 */ | |||
/* author: Andreas Baumgart */ | |||
/* last updated: 2019-02-21 */ | |||
/* ref: Kv52 (TM-C, Labor 5) */ | |||
/* description: finds the solution for */ | |||
/* the nonlinear IVP */ | |||
/*********************************************************/ | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
<!--------------------------------------------------------------------------------> | <!--------------------------------------------------------------------------------> | ||
{{MyCodeBlock|title=Declarations | {{MyCodeBlock|title=Declarations | ||
|text= | |text=Die System-Parameter sind | ||
::<math>\begin{array}{l}\mu_0 = 0.4\\\mu_1 = 0.2\\\alpha=15^{\circ}\end{array}</math>. | |||
Zum Dimensionslos-Machen der Bewegungsgleichungen brauchen wir später eine Bezugslänge ℓ''<sub>B</sub>'' und eine Bezugszeit ''t<sub>B</sub>'', die wir mit Hilfe der Eigenfrequenz der zugeordneten linearen Systems so wählen: | |||
::<math>\displaystyle \frac{k}{m} = \omega_0^2; \text{ , } \omega_0 = \frac{2 \pi}{t_B}</math> | |||
::(Achtung: das macht ''"1"''-periodische Lösungen) | |||
Die Bezugslänge wählen wir zusätzlich so, dass | |||
::<math>\displaystyle g= 1 \cdot \frac{\ell_B}{t_B^2}</math> | |||
[[Datei:Kv53-11.png|mini|Kennlinie]]Nun müssen wir zwei [[Sources/Lexikon/Kennlinie|Kennlinien]] definieren: die [[Sources/Lexikon/Kontaktkennlinie|Kontakt-Kennlinie]] mit der Feder und die [[Sources/Lexikon/Reibkennlinie|Reib-Kennlinie]] zwischen Körper und Ebene. | |||
Für den nichtlinearen Kontakt wählen wir | |||
::<math>K(\Delta\ell) = \left\{\begin{array}{cl}0&\text{ für } \Delta\ell< 0\\\displaystyle k \cdot \Delta\ell&\text{ sonst }\end{array}\right.</math> | |||
oder analog | |||
::<math>K(\Delta\ell) = k \cdot \displaystyle \frac{1}{2} \left( |\Delta\ell|+ \Delta\ell \right)</math>. | |||
Und für ''Δℓ'' =-u sieht sie dann so aus. | |||
Aus numerischer Sicht ist diese Kennlinie "Pfusch" - sie ist nicht stetig differenzierbar. Wenn wir also auf Probleme bei der Lösung stoßen - hier loht es sich, wieder einzusteigen . | |||
[[Datei:Kv53.png|mini|Reib-Kennlinie]]Bei der Reib-Kennlinie geben wir uns mehr Mühe - sie sei ein punktsymmetrisches Polynom | |||
::<math>\mu(v) = \mu_1 \cdot \left\{\begin{array}{cl}-1&\text{ wenn } v< -v_0 \text{ , }\\\displaystyle \sum_1^4 a_{2 i-1}\cdot v^{2 i-1}&\text{ wenn } -v_0<v< v_0 \text{ und }\\+1&\text{ sonst }\end{array}\right.</math> | |||
Und für die Parameter | |||
::<math>\begin{array}{l} \\\displaystyle {{a}_{1}}=\frac{25+160\cdot r}{54},\\\displaystyle{{a}_{3}}=-\frac{73+64\cdot r}{18},\\\displaystyle{{a}_{5}}=-\frac{16\cdot r-92}{9},\\\displaystyle{{a}_{7}}=\frac{64\cdot r-152}{27}\end{array}</math> | |||
mit | |||
::<math>\displaystyle r=\frac{\mu_0}{\mu_1}</math> | |||
erhalten wir die Kennlinie rechts: | |||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
1 | /* declarations */ | ||
declare("Δℓ", alphabetic); | |||
assume(g>0, mu[0]>0, mu[1]>0); | |||
/* parameter */ | |||
dimless: [[a[Bez] = g, solve(k/m = (2*%pi/t[Bez])^2,t[Bez])[2], l[Bez] = 1/2*a[Bez]*t[Bez]^2], | |||
['diff(u,t,2)=l[Bez]*'diff(U,tau,2)/t[Bez]^2, nu = V/epsilon, upsilon=U]]; | |||
params: [mu[1]=2/10,mu[0]=4/10,alpha=%pi/12, epsilon=1/10000, solve(g*t[Bez]^2/l[Bez] = 1,l[Bez])[1], solve((t[Bez]^2*k)/(2*m)=1000,m)[1]]; | |||
/**** define nonlinear friction characteristic ***/ | |||
/* choose generic polynom */ | |||
p : lsum(a[i]*nu^i,i,[1,3,5,7]); | |||
bcs : [subst([nu= 1 ], p ) = 1, | |||
subst([nu= 1 ], diff(p,nu)) = 0 , | |||
subst([nu= 1/2 ], diff(p,nu)) = 0 , | |||
subst([nu= 1/2 ], p ) = r]; | |||
coe : [a[1],a[3],a[5],a[7]]; | |||
charc : ratsimp(solve(subst(params,bcs),coe))[1]$ | |||
charc : append(charc, [r = subst(params, mu[0]/mu[1])]); | |||
mu(nu,charc) := if abs(nu)<1 then subst(charc, lsum(a[i]*nu^i,i,[1,3,5,7])) else signum(nu); | |||
plot2d(mu(nu,charc),[nu,-2,2], [xlabel,"ν →"], [ylabel,"μ →"])$ | |||
/**** define nonlinear friction characteristic ***/ | |||
K(upsilon):= (sqrt(upsilon^2)-upsilon)/2; | |||
plot2d(K(upsilon),[upsilon,-1,1])$ | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Equilibrium Conditions | |||
|text= | |||
Die Gleichgewichtsbeziehungen kommen aus dem Kräftegleichgewicht. Das Freikörperbild | |||
<table class="wikitable" style="background-color:white;"> | |||
<tr><td><br/><br/><br/><br/><br/><br/><br/>[[Datei:Kv53-12.png|rahmenlos|alternativtext=|60x60px]] | |||
</td><td>[[Datei:Kv53-13.png|rahmenlos|alternativtext=|180x180px]] | |||
</td></tr> | |||
</table> | |||
liefert die Bewegungsgleichung | |||
::<math>\displaystyle m \ddot{u}-k\cdot K(u) + m\,g\,\sin(\alpha) + R(v) = 0</math> | |||
< | mit | ||
::<math>R(v) = \mu(v)\,N, \;\; N = m\,g\,cos(\alpha)</math>. | |||
Mit den Bezugsgrößen und | |||
::<math>\displaystyle u = \ell_B \cdot U \text{ und } v = \frac{\ell_B}{t_B} \cdot V</math> | |||
finden wir als Bewegungsgleichung des Systems dann | |||
::<math>\displaystyle \frac{d^2}{d\tau^2} U + 2\, \pi^2 \left(U - |U|\right) + 2\,\sin(\alpha) + 2\,\cos(\alpha) \cdot \mu(\frac{V}{\epsilon})=0</math> | |||
< | |||
{{ | |||
| | |||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
1+1 | /*********************************************************/ | ||
/* define ODE in dim'less coordinate U */ | |||
eom : m*'diff(u,t,2) + m*g*sin(alpha) + m*g*cos(alpha)*mu[1]*mu(nu,charc) + k*l[Bez]*upsilon*K(upsilon)= 0; | |||
eom: [expand(subst(params,subst(dimless[2],eom))), 'diff(U,tau,1)=V]; | |||
dydt : solve(eom, ['diff(U,tau),'diff(U,tau,2)])[1]; | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
<!--------------------------------------------------------------------------------> | <!--------------------------------------------------------------------------------> | ||
{{MyCodeBlock|title=Solving | {{MyCodeBlock|title=Solving | ||
|text= | |text= | ||
Umschreiben in ein Differentialgleichungssystem erster Ordnung - wie wir es für die numerische Lösung brauchen - liefert | |||
::<math>\displaystyle \frac{d}{d\tau}\left(\begin{array}{c}U\\V\end{array}\right) = \left(\begin{array}{c}V\\\displaystyle - 2\, \pi^2 \left(U - |U|\right) - 2\,\sin(\alpha) - 2\,\cos(\alpha) \cdot \mu(\frac{V}{\epsilon})\end{array}\right)</math>. | |||
Mit den Anfangsbedingungen | |||
::<math>\begin{array}{l}U(0) = U_0\\V(0) = V_0\end{array}</math> | |||
erhalten wir aus einer Lösungsroutine nach dem [[Anfangswertprobleme/Methoden zur Lösung von Anfangswertproblemen/Runge-Kutta-Verfahren 4.ter Ordnung|Runge-Kutta-Verfahren 4.ter Ordnung]] das numerische Ergebnis. | |||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
1 | /*********************************************************/ | ||
/* numerical solution of IVP */ | |||
times : subst([t0 = 0, tmax = 15, dt = 0.01], | |||
[t, t0, tmax, dt]); | |||
stateVabs : [U,V]; | |||
dgl1stOrder : [rhs(dydt[1]),rhs(dydt[2])]; | |||
initiVals : [[1,0],[-0.1,0]]; | |||
/* solution of IVP (ivs) */ | |||
for i: 1 thru length(initiVals) do | |||
ivs[i] : rk(dgl1stOrder, stateVabs, initiVals[i], times)$ | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
== | <!--------------------------------------------------------------------------------> | ||
{{MyCodeBlock|title=Post-Processing | |||
|text= | |||
Wir tragen hier die Ergebnisse auf: | |||
<table class="wikitable" style="backgound:white;"> | <table class="wikitable" style="backgound:white;"> | ||
<tr><th></th><th></th></tr> | <tr><th>... in dieser Spalte für die Anfangsbedingungen <math>\begin{array}{l}U_0 = +1\\V_0 = 0\end{array}</math></th> | ||
<tr><td></td><td></td></tr> | <th>... in dieser Spalte für die Anfangsbedingungen <math>\begin{array}{l}U_0 = -0.1\\V_0 = 0\end{array}</math></th></tr> | ||
</table> | <tr><td>zunächst im Zeitbereich | ||
</td><td></td></tr><tr><td>[[Datei:Kv53-21.png|rahmenlos]]</td><td>[[Datei:Kv53-22.png|rahmenlos]]</td></tr></table> | |||
Im Phasenraum können wir beide Lösungen übereinander plotten: | |||
[[Datei:Kv53-23.png|alternativtext=|ohne|mini|Phasendiagramm (beide Lösungen)]] | |||
Und wir können uns die Reibkraft anschauen - mit den Spitzen, zu denen Haften auftritt:[[Datei:Kv53-15.png|mini|Reibkoeffizient ''μ''|alternativtext=|ohne]] | |||
Machen wir den WInkel der Ebene etwas flacher - hier ''α'' = 4° - so bleibt die Kiste im Umkehrpunkt liegen. Man sieht: sie haftet nicht wirklich, sondern rutscht nur sehr langsam die Ebene herunter. | |||
Damit wir den Effekt des "Haftens" genauer abbilden, können wir das ε noch kleiner machen. | |||
| | <table class="wikitable" style="backgound:white;"> | ||
<tr><th>Lösung im Zeitbereich für <math>\begin{array}{l}U_0 = +1\\V_0 = 0\end{array}</math></th> | |||
<th>Lösung im Phasenraum für <math>\begin{array}{l}U_0 = -0.1\\V_0 = 0\end{array}</math></th></tr> | |||
<tr><td>[[Datei:Kv53-31.png|rahmenlos]] | |||
</td><td>[[Datei:Kv53-32.png|rahmenlos]] | |||
</td></tr> | |||
</table>Zu dieser Lösung gehört die Reibkraft | |||
[[Datei:Kv53-33.png|mini|Reibkoeffizient ''μ''|ohne]] | |||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
1+1 | /*********************************************************/ | ||
/* plot results */ | |||
for i: 1 thru length(initiVals) do | |||
(T[i] : makelist(ivs[i][j][1],j,1,length(ivs[i])), | |||
uD[i] : makelist(ivs[i][j][2],j,1,length(ivs[i])), | |||
vD[i] : makelist(ivs[i][j][3],j,1,length(ivs[i])), | |||
mD[i] : makelist(subst(params,mu[1])*mu(ivs[i][j][3]/subst(params,epsilon),charc),j,1,length(ivs[i])), | |||
plot2d([discrete, T[i], uD[i]], | |||
[title, sconcat("start @: ",string(initiVals[i]))], | |||
[xlabel,"τ/1->"], [ylabel,"U/1->"])); | |||
/* phase plot */ | |||
curves : makelist([discrete,uD[i],vD[i]],i,1,length(initiVals))$ | |||
plot2d(curves, [legend, false], [x,-0.2,1.2], | |||
[ylabel,"V/1->"], [xlabel,"U/1->"], | |||
[legend, "first initial conditions", "second initial conditions"]); | |||
/* friction characteristic plot */ | |||
curves : makelist([discrete,T[i],mD[i]],i,1,length(initiVals))$ | |||
plot2d(curves, [legend, false], [y,-0.3,+0.3], | |||
[ylabel,"mu/1->"], [xlabel,"tau/1->"]); | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
'''Links''' | '''Links''' | ||
* ... | * ... | ||
Aktuelle Version vom 27. März 2021, 07:09 Uhr
Aufgabenstellung
Eine Kiste der Masse m bewegt sich auf einer schiefen Ebene, die unter dem Winkel α gegenüber der Horizontalen geneigt ist. Zwischen Kiste und Ebene wirkt eine Reibkraft (Haft-Koeffizient μ0, Reib-Koeffizient μ1). Zu Beginn der Bewegung wird die Kiste wie skizziert um den Betrag Δℓ in eine Feder der Steifigkeit k eingedrückt und dann losgelassen.
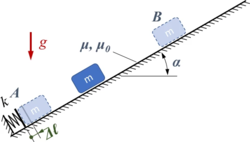
Gesucht ist die nichtlineare Bewegungsgleichung mit Reibkennlinie sowie die numerische Lösung als Anfangswertproblem.
Dabei sollen verschiedene Ergebnis-Muster gezeigt werden:
- die Kiste bleibt nach der ersten Aufwärts-Bewegung auf der Ebene bei B haften und bewegt sich nicht weiter.
- die Kiste erfährt mehrere Aufwärts- und Abwärts-Bewegungen, bevor sie liegen bleibt.
Lösung mit Maxima
Header
Wir stellen die Bewegungsgleichungen des Systems als System con Differentialgleichungen erster Ordnung auf. Die Nichtlinearität kommt aus der Reibkraft und dem "Abheben" der Kiste von der Feder.
/*********************************************************/
/* MAXIMA script */
/* version: wxMaxima 15.08.2 */
/* author: Andreas Baumgart */
/* last updated: 2019-02-21 */
/* ref: Kv52 (TM-C, Labor 5) */
/* description: finds the solution for */
/* the nonlinear IVP */
/*********************************************************/
Declarations
Die System-Parameter sind
- .
Zum Dimensionslos-Machen der Bewegungsgleichungen brauchen wir später eine Bezugslänge ℓB und eine Bezugszeit tB, die wir mit Hilfe der Eigenfrequenz der zugeordneten linearen Systems so wählen:
- (Achtung: das macht "1"-periodische Lösungen)
Die Bezugslänge wählen wir zusätzlich so, dass
Nun müssen wir zwei Kennlinien definieren: die Kontakt-Kennlinie mit der Feder und die Reib-Kennlinie zwischen Körper und Ebene.
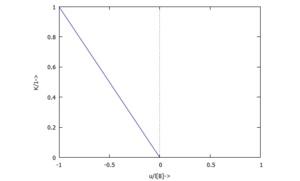
Für den nichtlinearen Kontakt wählen wir
oder analog
- .
Und für Δℓ =-u sieht sie dann so aus.
Aus numerischer Sicht ist diese Kennlinie "Pfusch" - sie ist nicht stetig differenzierbar. Wenn wir also auf Probleme bei der Lösung stoßen - hier loht es sich, wieder einzusteigen .
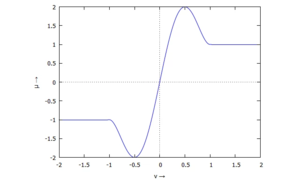
Bei der Reib-Kennlinie geben wir uns mehr Mühe - sie sei ein punktsymmetrisches Polynom
Und für die Parameter
mit
erhalten wir die Kennlinie rechts:
/* declarations */
declare("Δℓ", alphabetic);
assume(g>0, mu[0]>0, mu[1]>0);
/* parameter */
dimless: [[a[Bez] = g, solve(k/m = (2*%pi/t[Bez])^2,t[Bez])[2], l[Bez] = 1/2*a[Bez]*t[Bez]^2],
['diff(u,t,2)=l[Bez]*'diff(U,tau,2)/t[Bez]^2, nu = V/epsilon, upsilon=U]];
params: [mu[1]=2/10,mu[0]=4/10,alpha=%pi/12, epsilon=1/10000, solve(g*t[Bez]^2/l[Bez] = 1,l[Bez])[1], solve((t[Bez]^2*k)/(2*m)=1000,m)[1]];
/**** define nonlinear friction characteristic ***/
/* choose generic polynom */
p : lsum(a[i]*nu^i,i,[1,3,5,7]);
bcs : [subst([nu= 1 ], p ) = 1,
subst([nu= 1 ], diff(p,nu)) = 0 ,
subst([nu= 1/2 ], diff(p,nu)) = 0 ,
subst([nu= 1/2 ], p ) = r];
coe : [a[1],a[3],a[5],a[7]];
charc : ratsimp(solve(subst(params,bcs),coe))[1]$
charc : append(charc, [r = subst(params, mu[0]/mu[1])]);
mu(nu,charc) := if abs(nu)<1 then subst(charc, lsum(a[i]*nu^i,i,[1,3,5,7])) else signum(nu);
plot2d(mu(nu,charc),[nu,-2,2], [xlabel,"ν →"], [ylabel,"μ →"])$
/**** define nonlinear friction characteristic ***/
K(upsilon):= (sqrt(upsilon^2)-upsilon)/2;
plot2d(K(upsilon),[upsilon,-1,1])$
Equilibrium Conditions
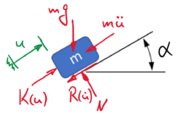
Die Gleichgewichtsbeziehungen kommen aus dem Kräftegleichgewicht. Das Freikörperbild
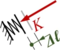
| 
|
liefert die Bewegungsgleichung
mit
- .
Mit den Bezugsgrößen und
finden wir als Bewegungsgleichung des Systems dann
/*********************************************************/
/* define ODE in dim'less coordinate U */
eom : m*'diff(u,t,2) + m*g*sin(alpha) + m*g*cos(alpha)*mu[1]*mu(nu,charc) + k*l[Bez]*upsilon*K(upsilon)= 0;
eom: [expand(subst(params,subst(dimless[2],eom))), 'diff(U,tau,1)=V];
dydt : solve(eom, ['diff(U,tau),'diff(U,tau,2)])[1];
Solving
Umschreiben in ein Differentialgleichungssystem erster Ordnung - wie wir es für die numerische Lösung brauchen - liefert
- .
Mit den Anfangsbedingungen
erhalten wir aus einer Lösungsroutine nach dem Runge-Kutta-Verfahren 4.ter Ordnung das numerische Ergebnis.
/*********************************************************/
/* numerical solution of IVP */
times : subst([t0 = 0, tmax = 15, dt = 0.01],
[t, t0, tmax, dt]);
stateVabs : [U,V];
dgl1stOrder : [rhs(dydt[1]),rhs(dydt[2])];
initiVals : [[1,0],[-0.1,0]];
/* solution of IVP (ivs) */
for i: 1 thru length(initiVals) do
ivs[i] : rk(dgl1stOrder, stateVabs, initiVals[i], times)$
Post-Processing
Wir tragen hier die Ergebnisse auf:
| ... in dieser Spalte für die Anfangsbedingungen | ... in dieser Spalte für die Anfangsbedingungen |
|---|---|
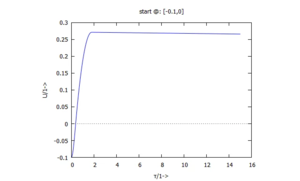
| zunächst im Zeitbereich | |
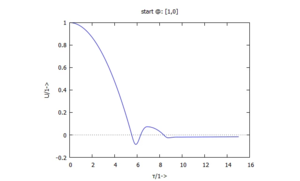 | 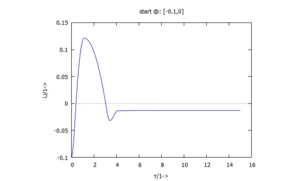 |
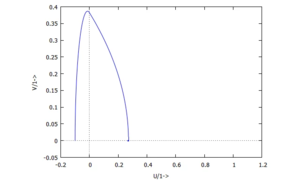
Im Phasenraum können wir beide Lösungen übereinander plotten:
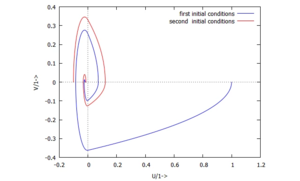
Und wir können uns die Reibkraft anschauen - mit den Spitzen, zu denen Haften auftritt:
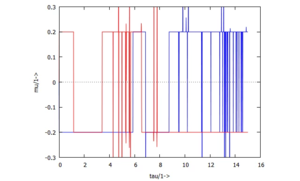
Machen wir den WInkel der Ebene etwas flacher - hier α = 4° - so bleibt die Kiste im Umkehrpunkt liegen. Man sieht: sie haftet nicht wirklich, sondern rutscht nur sehr langsam die Ebene herunter.
Damit wir den Effekt des "Haftens" genauer abbilden, können wir das ε noch kleiner machen.
| Lösung im Zeitbereich für | Lösung im Phasenraum für |
|---|---|
| 
|
Zu dieser Lösung gehört die Reibkraft
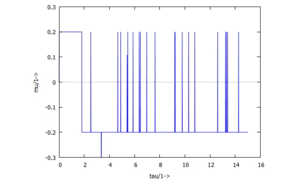
/*********************************************************/
/* plot results */
for i: 1 thru length(initiVals) do
(T[i] : makelist(ivs[i][j][1],j,1,length(ivs[i])),
uD[i] : makelist(ivs[i][j][2],j,1,length(ivs[i])),
vD[i] : makelist(ivs[i][j][3],j,1,length(ivs[i])),
mD[i] : makelist(subst(params,mu[1])*mu(ivs[i][j][3]/subst(params,epsilon),charc),j,1,length(ivs[i])),
plot2d([discrete, T[i], uD[i]],
[title, sconcat("start @: ",string(initiVals[i]))],
[xlabel,"τ/1->"], [ylabel,"U/1->"]));
/* phase plot */
curves : makelist([discrete,uD[i],vD[i]],i,1,length(initiVals))$
plot2d(curves, [legend, false], [x,-0.2,1.2],
[ylabel,"V/1->"], [xlabel,"U/1->"],
[legend, "first initial conditions", "second initial conditions"]);
/* friction characteristic plot */
curves : makelist([discrete,T[i],mD[i]],i,1,length(initiVals))$
plot2d(curves, [legend, false], [y,-0.3,+0.3],
[ylabel,"mu/1->"], [xlabel,"tau/1->"]);
Links
- ...
Literature
- ...