Gelöste Aufgaben/Kit6: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 20: | Zeile 20: | ||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
/*******************************************************/ | |||
/* MAXIMA script */ | |||
/* version: wxMaxima 15.08.2 */ | |||
/* author: Andreas Baumgart */ | |||
/* last updated: 2017-10-12 */ | |||
/* ref: Lösung des Randwertproblems */ | |||
/*******************************************************/ | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
= | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Preparations | |||
|text= | |||
Stützstellen (Samples) eines Funktionsverlaufs erhalten wir, wenn wir die Funktion | Stützstellen (Samples) eines Funktionsverlaufs erhalten wir, wenn wir die Funktion | ||
| Zeile 32: | Zeile 41: | ||
Das Bild oben zeigt die N= 16 Samples zu dieser Funktion. | Das Bild oben zeigt die N= 16 Samples zu dieser Funktion. | ||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
/*******************************************************/ | |||
declare("Δξ", alphabetic); | |||
params: [l[2]=l[1]/2, | |||
w = [(5*xi^4)/2-(194*xi^3)/27+5*xi^2+xi, | |||
(19*xi^3)/54-(7*xi^2)/18-(5*xi)/18+71/54]]; | |||
nos: 5; | |||
samples: [ | |||
makelist(i/(2*nos),i,0,3*nos), | |||
append(makelist(subst(i/(2*nos),xi,subst(params,w)[1]),i,0,2*nos), | |||
makelist(subst(i/( nos),xi,subst(params,w)[2]),i,1, nos))]; | |||
plot2d ([discrete, samples[1], samples[2]], | |||
[style,points], [point_type,diamond], [color,black], | |||
[xlabel, "ξ→"], [ylabel, "w/W→"])$ | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
= | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Generic Approximation Polynoms | |||
|text= | |||
Diese Samples können wir in der Umgebung eines Punktes durch Polynome approximieren - z.B. durch eine Geradengleichung. Je nach Anwendungszweck braucht man Polynome einer bestimmten Ordnung. Um z.B. die zweite Ableitung ''w<nowiki>''</nowiki>(ξ<sup>*</sup>)'' zu bestimmen, brauchen wir mindestens ein Polynom 2. Grades, das dann zweimal abgeleitet die konstante Krümmung liefert. | Diese Samples können wir in der Umgebung eines Punktes durch Polynome approximieren - z.B. durch eine Geradengleichung. Je nach Anwendungszweck braucht man Polynome einer bestimmten Ordnung. Um z.B. die zweite Ableitung ''w<nowiki>''</nowiki>(ξ<sup>*</sup>)'' zu bestimmen, brauchen wir mindestens ein Polynom 2. Grades, das dann zweimal abgeleitet die konstante Krümmung liefert. | ||
Wir nehmen gleich einen ganzen Schwung von Polynomen, hier bis zur Ordnung 4. Je nach Ordnung des gesuchten Polynoms haben wir unterschiedlich viele unbekannte Polynomial-Koeffizienten. Diese müssen wir durch Anpassen an die Samples in der Umgebung von ''ξ<sup>*</sup>'' bestimmen. | Wir nehmen gleich einen ganzen Schwung von Polynomen, hier bis zur Ordnung 4. Je nach Ordnung des gesuchten Polynoms haben wir unterschiedlich viele unbekannte Polynomial-Koeffizienten. Diese müssen wir durch Anpassen an die Samples in der Umgebung von ''ξ<sup>*</sup>'' bestimmen. | ||
<math>\begin{array}{lcl} p_0(\tilde{\xi})&=& W_0\\ p_1(\tilde{\xi})&=& \displaystyle \frac{{{W}_{-1}}+{{W}_{1}}}{2}-\frac{\left( {{W}_{-1}}-{{W}_{1}}\right) \cdot \xi}{2\cdot \Delta\xi}\\ p_2(\tilde{\xi})&=& \displaystyle -\frac{\left( {{W}_{-1}}-{{W}_{1}}\right) \cdot \xi}{2\cdot \Delta\xi}+\frac{\left( {{W}_{-1}}-2\cdot {{W}_{0}}+{{W}_{1}}\right) \cdot {{\xi}^{2}}}{2\cdot {{\Delta\xi}^{2}}}+{{W}_{0}}\\ p_3(\tilde{\xi})&=& \displaystyle \frac{\left( {{W}_{-2}}-8\cdot {{W}_{-1}}+8\cdot {{W}_{1}}-{{W}_{2}}\right) \cdot \xi}{12\cdot \Delta\xi}+\frac{\left( {{W}_{-2}}-{{W}_{-1}}-{{W}_{1}}+{{W}_{2}}\right) \cdot {{\xi}^{2}}}{6\cdot {{\Delta\xi}^{2}}}-\frac{\left( {{W}_{-2}}-2\cdot {{W}_{-1}}+2\cdot {{W}_{1}}-{{W}_{2}}\right) \cdot {{\xi}^{3}}}{12\cdot {{\Delta\xi}^{3}}}-\frac{{{W}_{-2}}-4\cdot {{W}_{-1}}-4\cdot {{W}_{1}}+{{W}_{2}}}{6}\\ p_4(\tilde{\xi})&=& \displaystyle \frac{\left( W_{-2}-8 \cdot W_{-1}+8\cdot W_{1}-W_{2}\right) \cdot \xi}{12\cdot \Delta\xi}-\frac{\left( {{W}_{-2}}-16\cdot {{W}_{-1}}+30\cdot {{W}_{0}}-16\cdot {{W}_{1}}+{{W}_{2}}\right) \cdot {{\xi}^{2}}}{24\cdot {{\Delta\xi}^{2}}}-\frac{\left( {{W}_{-2}}-2\cdot {{W}_{-1}}+2\cdot {{W}_{1}}-{{W}_{2}}\right) \cdot {{\xi}^{3}}}{12\cdot {{\Delta\xi}^{3}}}+\frac{\left( {{W}_{-2}}-4\cdot {{W}_{-1}}+6\cdot {{W}_{0}}-4\cdot {{W}_{1}}+{{W}_{2}}\right) \cdot {{\xi}^{4}}}{24\cdot {{\Delta\xi}^{4}}}+{{W}_{0}}\\ \end{array}</math> | ::<math>\begin{array}{lcl} p_0(\tilde{\xi})&=& W_0\\ p_1(\tilde{\xi})&=& \displaystyle \frac{{{W}_{-1}}+{{W}_{1}}}{2}-\frac{\left( {{W}_{-1}}-{{W}_{1}}\right) \cdot \xi}{2\cdot \Delta\xi}\\ p_2(\tilde{\xi})&=& \displaystyle -\frac{\left( {{W}_{-1}}-{{W}_{1}}\right) \cdot \xi}{2\cdot \Delta\xi}+\frac{\left( {{W}_{-1}}-2\cdot {{W}_{0}}+{{W}_{1}}\right) \cdot {{\xi}^{2}}}{2\cdot {{\Delta\xi}^{2}}}+{{W}_{0}}\\ p_3(\tilde{\xi})&=& \displaystyle \frac{\left( {{W}_{-2}}-8\cdot {{W}_{-1}}+8\cdot {{W}_{1}}-{{W}_{2}}\right) \cdot \xi}{12\cdot \Delta\xi}+\frac{\left( {{W}_{-2}}-{{W}_{-1}}-{{W}_{1}}+{{W}_{2}}\right) \cdot {{\xi}^{2}}}{6\cdot {{\Delta\xi}^{2}}}-\frac{\left( {{W}_{-2}}-2\cdot {{W}_{-1}}+2\cdot {{W}_{1}}-{{W}_{2}}\right) \cdot {{\xi}^{3}}}{12\cdot {{\Delta\xi}^{3}}}-\frac{{{W}_{-2}}-4\cdot {{W}_{-1}}-4\cdot {{W}_{1}}+{{W}_{2}}}{6}\\ p_4(\tilde{\xi})&=& \displaystyle \frac{\left( W_{-2}-8 \cdot W_{-1}+8\cdot W_{1}-W_{2}\right) \cdot \xi}{12\cdot \Delta\xi}-\frac{\left( {{W}_{-2}}-16\cdot {{W}_{-1}}+30\cdot {{W}_{0}}-16\cdot {{W}_{1}}+{{W}_{2}}\right) \cdot {{\xi}^{2}}}{24\cdot {{\Delta\xi}^{2}}}-\frac{\left( {{W}_{-2}}-2\cdot {{W}_{-1}}+2\cdot {{W}_{1}}-{{W}_{2}}\right) \cdot {{\xi}^{3}}}{12\cdot {{\Delta\xi}^{3}}}+\frac{\left( {{W}_{-2}}-4\cdot {{W}_{-1}}+6\cdot {{W}_{0}}-4\cdot {{W}_{1}}+{{W}_{2}}\right) \cdot {{\xi}^{4}}}{24\cdot {{\Delta\xi}^{4}}}+{{W}_{0}}\\ \end{array}</math> | ||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
1 | /*******************************************************/ | ||
poly : makelist(sum(c[i,j]*xi^j,j,0,i),i,0,4); | |||
pick : [[0],[-1,1],[-1,0,1],[-2,-1,1,2],[-2,-1,0,1,2]]; | |||
coeffs: flatten(makelist( | |||
solve(makelist(subst(pick[i][j]*Δξ,xi,poly[i]) = W[pick[i][j]],j,1,length(pick[i])), | |||
makelist(c[i-1,j],j,0,length(pick[i])-1))[1], | |||
i,1,5)); | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
<!--------------------------------------------------------------------------------> | <!--------------------------------------------------------------------------------> | ||
{{MyCodeBlock|title=Approximation Polynoms for ξ=8∙Δξ | {{MyCodeBlock|title=Approximation Polynoms for ξ=8∙Δξ | ||
|text= | |text= | ||
Grafen der 5 Polynome nullten bis vierten Grades zeigen die folgende Grafen: | |||
[[Datei:Kig6-12.png|ohne|mini|Polynom-Approximation]] | |||
[[Datei:Kig6-13.png|ohne|mini|Polynom-Approximation (Detail)]] | |||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
1+1 | /*******************************************************/ | ||
key : 8; | |||
selec : makelist( W[i] = samples[2][key+1+i],i,-2,2); | |||
toPlot : subst([Δξ = 3/2/(3*nos)],subst(selec,subst(coeffs,poly))); | |||
toPlot : append([[discrete, samples[1], samples[2]]], | |||
makelist([parametric, t+key*3/2/(3*nos), subst(t,xi,toPlot[i]), [t,-1/2,1/2]],i,1,5)); | |||
plot2d (toPlot, | |||
[style,points,lines,lines,lines,lines,lines], | |||
[point_type,diamond], | |||
[color,black, gray, blue,green, red, magenta], | |||
[legend, "w", "p[0]", "p[1]", "p[2]", "p[3]", "p[4]"], | |||
[xlabel, "ξ→"], [ylabel, "w/W→"])$ | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
= | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Check for fourth order derivative | |||
|text= | |||
Wir prüfen die Übereinstimmung mit der Problemstellung aus [[Gelöste Aufgaben/Kit5|Kit5]]. Es muss | Wir prüfen die Übereinstimmung mit der Problemstellung aus [[Gelöste Aufgaben/Kit5|Kit5]]. Es muss | ||
<math>\begin{array}{l} w''''(\xi) = \mu \text{ für } 0\le \xi < 1 \\ w''''(\xi) = 0 \text{ sonst }\end{array}</math> | ::<math>\begin{array}{l} w''''(\xi) = \mu \text{ für } 0\le \xi < 1 \\ w''''(\xi) = 0 \text{ sonst }\end{array}</math> | ||
gelten.[[Datei:Kig6-14.png|mini|Vierte Ableitung w<nowiki>''''</nowiki>]]Dafür definieren wir | gelten.[[Datei:Kig6-14.png|mini|Vierte Ableitung w<nowiki>''''</nowiki>]]Dafür definieren wir | ||
<math>\begin{array}{ll} \kappa &:= \displaystyle \frac{d^4 p_4}{d\xi^4} \\ & = \displaystyle \frac{{{W}_{-2}}-4\cdot {{W}_{-1}}+6\cdot {{W}_{0}}-4\cdot {{W}_{1}}+{{W}_{2}}}{{{\mathit{\Delta \xi}}^{4}}} \end{array}</math> | ::<math>\begin{array}{ll} \kappa &:= \displaystyle \frac{d^4 p_4}{d\xi^4} \\ & = \displaystyle \frac{{{W}_{-2}}-4\cdot {{W}_{-1}}+6\cdot {{W}_{0}}-4\cdot {{W}_{1}}+{{W}_{2}}}{{{\mathit{\Delta \xi}}^{4}}} \end{array}</math> | ||
und ermitteln die vierte Ableitung aus 5 aufeinanderfolgenden Sampling-Punkten. | und ermitteln die vierte Ableitung aus 5 aufeinanderfolgenden Sampling-Punkten. | ||
| Zeile 83: | Zeile 124: | ||
Das funktioniert für die Samples 3,4, ... N-2 (damit jeweils "rechts" und "links" 2 Samples zur Verfügung stehen) und tragen ''κ'' rechts auf: | Das funktioniert für die Samples 3,4, ... N-2 (damit jeweils "rechts" und "links" 2 Samples zur Verfügung stehen) und tragen ''κ'' rechts auf: | ||
Für die analytische richtige Lösung müsste die vierte Ableitung ''κ'' einen Sprung an der Stelle ''ξ=1'' haben. Weil sich diese Ableitung jedoch aus fünf aufeinanderfolgenden Stützstellen ergibt, funktioniert das nicht. | Für die analytische richtige Lösung müsste die vierte Ableitung ''κ'' einen Sprung an der Stelle ''ξ=1'' haben. Weil sich diese Ableitung jedoch aus fünf aufeinanderfolgenden Stützstellen ergibt, funktioniert das nicht. | ||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
1+1 | /* Check */ | ||
kappa : subst([Δξ=1/10],diff(subst(coeffs,poly[5]),xi,4)); | |||
samplePoints : makelist(i,i,3,length(samples[2])-2); | |||
select5 : makelist(makelist(W[j]=samples[2][i+j],j,-2,2),i,samplePoints); | |||
plot2d([discrete, samplePoints/10-1/10, makelist(subst(select5[i],kappa),i,1,length(select5))], | |||
[style,points], | |||
[point_type,diamond], | |||
[color,red], | |||
[legend, "κ"], | |||
[xlabel, "ξ→"], [x,0,1.5], [ylabel, "w''''"])$; | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
<hr/> | <hr/> | ||
Aktuelle Version vom 26. März 2021, 07:32 Uhr
Aufgabenstellung
Von einen Funktionsverlauf (hier aus Kit5) wurden die skizzierten Samples ermittelt, aus denen bzgl. eines Referenzpunktes die Ableitungen bis zur vierten Ordnung ermittelt werden sollen.
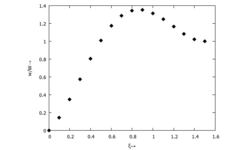
Gesucht ist eine numerische Approximation der Ableitungen bis zur vierten Ordnung aus Samples der Lösung eines Randwertproblems.
Hier wird der Bezug zur Methode der Finiten Differenzen gezeigt.
Lösung mit Maxima
Header
Der Funktionsverlauf für dieses Beispiel kommt aus Aufgabe Kit4.
/*******************************************************/
/* MAXIMA script */
/* version: wxMaxima 15.08.2 */
/* author: Andreas Baumgart */
/* last updated: 2017-10-12 */
/* ref: Lösung des Randwertproblems */
/*******************************************************/
Preparations
Stützstellen (Samples) eines Funktionsverlaufs erhalten wir, wenn wir die Funktion
in regelmäßigen Intervallen abtasten.
Das Bild oben zeigt die N= 16 Samples zu dieser Funktion.
/*******************************************************/
declare("Δξ", alphabetic);
params: [l[2]=l[1]/2,
w = [(5*xi^4)/2-(194*xi^3)/27+5*xi^2+xi,
(19*xi^3)/54-(7*xi^2)/18-(5*xi)/18+71/54]];
nos: 5;
samples: [
makelist(i/(2*nos),i,0,3*nos),
append(makelist(subst(i/(2*nos),xi,subst(params,w)[1]),i,0,2*nos),
makelist(subst(i/( nos),xi,subst(params,w)[2]),i,1, nos))];
plot2d ([discrete, samples[1], samples[2]],
[style,points], [point_type,diamond], [color,black],
[xlabel, "ξ→"], [ylabel, "w/W→"])$
Generic Approximation Polynoms
Diese Samples können wir in der Umgebung eines Punktes durch Polynome approximieren - z.B. durch eine Geradengleichung. Je nach Anwendungszweck braucht man Polynome einer bestimmten Ordnung. Um z.B. die zweite Ableitung w''(ξ*) zu bestimmen, brauchen wir mindestens ein Polynom 2. Grades, das dann zweimal abgeleitet die konstante Krümmung liefert.
Wir nehmen gleich einen ganzen Schwung von Polynomen, hier bis zur Ordnung 4. Je nach Ordnung des gesuchten Polynoms haben wir unterschiedlich viele unbekannte Polynomial-Koeffizienten. Diese müssen wir durch Anpassen an die Samples in der Umgebung von ξ* bestimmen.
/*******************************************************/
poly : makelist(sum(c[i,j]*xi^j,j,0,i),i,0,4);
pick : [[0],[-1,1],[-1,0,1],[-2,-1,1,2],[-2,-1,0,1,2]];
coeffs: flatten(makelist(
solve(makelist(subst(pick[i][j]*Δξ,xi,poly[i]) = W[pick[i][j]],j,1,length(pick[i])),
makelist(c[i-1,j],j,0,length(pick[i])-1))[1],
i,1,5));
Approximation Polynoms for ξ=8∙Δξ
Grafen der 5 Polynome nullten bis vierten Grades zeigen die folgende Grafen:
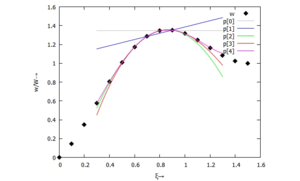
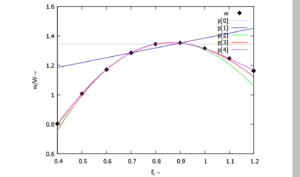
/*******************************************************/
key : 8;
selec : makelist( W[i] = samples[2][key+1+i],i,-2,2);
toPlot : subst([Δξ = 3/2/(3*nos)],subst(selec,subst(coeffs,poly)));
toPlot : append([[discrete, samples[1], samples[2]]],
makelist([parametric, t+key*3/2/(3*nos), subst(t,xi,toPlot[i]), [t,-1/2,1/2]],i,1,5));
plot2d (toPlot,
[style,points,lines,lines,lines,lines,lines],
[point_type,diamond],
[color,black, gray, blue,green, red, magenta],
[legend, "w", "p[0]", "p[1]", "p[2]", "p[3]", "p[4]"],
[xlabel, "ξ→"], [ylabel, "w/W→"])$
Check for fourth order derivative
Wir prüfen die Übereinstimmung mit der Problemstellung aus Kit5. Es muss
gelten.
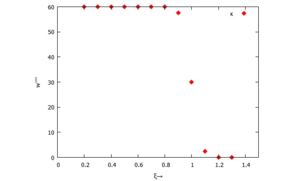
Dafür definieren wir
und ermitteln die vierte Ableitung aus 5 aufeinanderfolgenden Sampling-Punkten.
Das funktioniert für die Samples 3,4, ... N-2 (damit jeweils "rechts" und "links" 2 Samples zur Verfügung stehen) und tragen κ rechts auf:
Für die analytische richtige Lösung müsste die vierte Ableitung κ einen Sprung an der Stelle ξ=1 haben. Weil sich diese Ableitung jedoch aus fünf aufeinanderfolgenden Stützstellen ergibt, funktioniert das nicht.
/* Check */
kappa : subst([Δξ=1/10],diff(subst(coeffs,poly[5]),xi,4));
samplePoints : makelist(i,i,3,length(samples[2])-2);
select5 : makelist(makelist(W[j]=samples[2][i+j],j,-2,2),i,samplePoints);
plot2d([discrete, samplePoints/10-1/10, makelist(subst(select5[i],kappa),i,1,length(select5))],
[style,points],
[point_type,diamond],
[color,red],
[legend, "κ"],
[xlabel, "ξ→"], [x,0,1.5], [ylabel, "w''''"])$;
Links
- ...
Literature
- ...