Gelöste Aufgaben/Kw30: Unterschied zwischen den Versionen
Die Seite wurde neu angelegt: „m“ |
Keine Bearbeitungszusammenfassung |
||
| (12 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
m | [[Category:Gelöste Aufgaben]] | ||
[[Category:A*x=b]] | |||
[[Category:Lineare Algebra]] | |||
[[Category:Numerische Lösung]] | |||
[[Category:Anfangswertproblem]] | |||
[[Category:Feder-Masse-System]] | |||
[[Category:Eigenwert]][[Category:Eigenwertproblem]] | |||
[[Category:Floquet-Theorem]] | |||
[[Category:Fundamentalmatrix]] | |||
[[Category:Mathieusche Differentialgleichung]] | |||
[[Category:Maxima]] | |||
[[Category:Stabilität]] | |||
==Aufgabenstellung== | |||
Manchmal stößt man in unscheinbaren Aufgabenstellungen auf unerwartete Hindernisse - so in dieser Aufgabe eines mathematischen Pendels, die auf eine Bewegungsgleichung mit periodischen Koeffizienten führt. | |||
<onlyinclude> | |||
[[Datei:Kw30-01.png|alternativtext=|links|mini|208x208px|Lageplan]] | |||
Das Pendel der Masse ''m'' und Länge ''ℓ'' der Aufgabe hat einen in ''A'' senkrecht mit ''u(t)'' periodisch bewegten Aufhängepunkt. | |||
Berechnen Sie die Stabilität der Lösung der linearisierten Bewegungsgleichung für verschiedene Parameterkombinationen. | |||
</onlyinclude> | |||
Gegeben sind | |||
* ''m, ℓ, g'' sowie | |||
* <math>u(t) = \hat{u} \cdot \cos(\Omega\;t)</math> | |||
== Lösung mit Maxima == | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Equations of Motion | |||
|text= | |||
[[Datei:Kw30.png|mini|Koordinaten und Freikörperbild|alternativtext=|261x261px]] | |||
Aus dem Freikörperbild erhalten wir die Bewegungsgleichung | |||
::<math>\displaystyle J\ddot{\varphi}+\frac{\ell}{2}\;m\;\frac{\ell}{2}\;\ddot{\varphi} + m\;(g-\ddot{u})\; \frac{\ell}{2}\; \sin(\varphi) = 0</math> | |||
mit | |||
::<math>\displaystyle \dot{(.)} := \frac{d}{dt} (.)</math>. | |||
Wir linearisieren und erhalten mit | |||
::<math>\displaystyle \sin(\varphi) \approx \varphi,\;\; J = \frac{m\;\ell^2}{12}</math> | |||
die lineare Differentialgleichung mit perdiodischen Koeffizienten | |||
::<math>\displaystyle \frac{1}{3} m\cdot {{\ell}^{2}}\cdot \ddot{\varphi}+m\cdot \ell\cdot \left( g + \Omega^2\;\hat{u}\;\cos(\Omega\;t)\right) \cdot \varphi=0</math>. | |||
Das ist eine Grundform der [https://de.wikipedia.org/wiki/Mathieusche_Differentialgleichung Mathieuschen Differentialgleichung] - die wir noch in dimensionslose Form bringen wollen. Dazu soll die zugeordnete gewöhnliche Differentialgleichung mit konstanten Koeffizienten, also für | |||
::<math>\hat{u}=0</math>, | |||
in dimensionsloser Schreibweise und für einfache Parameter-Konstellationen die Periodendauer "1" haben. Das erreichen mit der dimensionslosen Zeit | |||
::<math>\displaystyle t = T\cdot\tau \text{ und } \Omega=\frac{2\pi}{T}</math> | |||
und den dimensionslosen Parametern | |||
::<math>\displaystyle \Lambda = \frac{3\;g}{\Omega^2\;\ell} \text{ und } \Gamma = \frac{3\;U}{\ell}</math>. | |||
Damit ist | |||
::<math>\displaystyle \varphi'' + (2\pi)^2\cdot \left( \Lambda + \Gamma\cdot \cos(2\pi\; \tau)\right) \cdot\varphi = 0 \text{ mit } (.)' := \frac{d}{d\tau}(.)</math>. | |||
Für ''Λ=1'' ist das wie gewünscht eine Bewegungsgleichung mit der Periodendauer "1": | |||
::<math>\varphi'' + (2\pi)^2\;\varphi = 0</math>. | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
/*********************************************************/ | |||
/* MAXIMA script */ | |||
/* version: wxMaxima 15.08.2 */ | |||
/* author: Andreas Baumgart */ | |||
/* last updated: 2018-12-30 */ | |||
/* ref: Kw30 */ | |||
/* description: finds the solution for */ | |||
/* Mathieus Differential Equation */ | |||
/*********************************************************/ | |||
/*********************************************************/ | |||
declare("ℓ", alphabetic); | |||
load(eigen)$ | |||
/*load (lapack)$*/ | |||
/* declare parameters */ | |||
params: [J=m*ℓ^2/12, Omega=2*%pi/T, Lambda = (3*g)/(Omega^2*ℓ), Gamma = (3*U)/ℓ]; | |||
/*********************************************************/ | |||
/* equations of motion */ | |||
eom: J*'diff(phi,t,2) + ℓ/2*m*ℓ/2*'diff(phi,t,2)*cos(phi) + m*(g-'diff(u,t,2))*ℓ*sin(phi) = 0; | |||
linearize : [sin(phi) = phi, cos(phi) = 1]; | |||
eom : subst(params,subst(linearize,eom)); | |||
eom : subst(['diff(phi,t,2) = 'diff(p,tau,2)/T^2,subst(params,'diff(u,t,2) = diff(U*cos(Omega*t),t,2)), t=T*tau],eom); | |||
eom : expand(subst(solve(rest(params, 1),[T,g,U]),eom*12*%pi^2/m/ℓ^2/Omega^2)); | |||
eom : ['diff(p,t) = v, | |||
'diff(v,t) = subst([phi=p,tau=t],subst(solve(eom, 'diff(p,tau,2))[1],'diff(p,tau,2)))]; | |||
</syntaxhighlight> | |||
}} | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Solve and Check for Stability of Solution | |||
|text= | |||
Für die Stabilität der Bewegungsgleichung brauchen wir den Satz von [[Sources/Lexikon/Satz von Floquet-Ljapunow|Floquet-Ljapunow]] und die Fundamentalmatrix ''Φ''. Zunächst schreiben wir die Bewegungsgleichung als Differentialgleichung erster Ordnung als | |||
::<math>\underline{q}' = \left(\begin{array}{c}\psi\\-(2\pi)^2\cdot \left( \Lambda + \Gamma\cdot \cos(2\pi\; \tau)\right) \cdot\varphi\end{array}\right) \text{ mit } \underline{q} = \left(\begin{array}{c}\varphi\\\psi\end{array}\right)</math> | |||
bzw. als | |||
::<math>\underline{q}' = \underbrace{\left(\begin{array}{c}0&1\\-(2\pi)^2\cdot \left( \Lambda + \Gamma\cdot \cos(2\pi\; \tau)\right) & 0\end{array}\right)}_{\displaystyle := \underline{\underline{A(\tau)}}} \cdot \underline{q}</math>. | |||
Durch den Zeit-periodischen Koeffizienten in ''τ'' hat diese Bewegungsgleichung keine "einfachen" Lösungen der Form e<sup>λt</sup> mehr. Statt dessen untersuchen wir die Stabilität anhand der Fundamentalmatrix ''Φ<sup>*</sup>'', in der zwei Fundamentalösungen | |||
::<math>\underline{\underline{\Phi}} := \left(\underline{q}_{T,1}, \underline{q}_{T,2}\right)</math> | |||
mit | |||
::<math>\underline{q}_{T,1} = \underline{q}_1(T) \text {und } \underline{q}_1(0) = \left(\begin{array}{c}1\\0 \end{array}\right)</math> | |||
und | |||
::<math>\underline{q}_{T,2} = \underline{q}_2(T) \text {und } \underline{q}_2(0) = \left(\begin{array}{c}0\\1 \end{array}\right)</math> | |||
stehen.[[Datei:Kw30-11.png|mini|Abbildungsvorschrift über die Periodendauer.|alternativtext=]] | |||
Wir interpretieren also die Fundamentalmatrix ''Φ<sup>*</sup>'' als Abbildungsvorschrift, um die Anfangsbedingungen ''q(0)'' über das Zeitintervall - hier ''T = 1'' - hinweg abzubilden. | |||
Die [[Werkzeuge/Lösungsbausteine der Mathematik/Eigenwertprobleme|Eigenwerte]] ''μ<sub>i</sub>'' der Fundamentalmatrix heißen | |||
* charakteristische Multiplikatoren. | |||
Die charakteristischen Exponenten sind | |||
* <math>\varrho_i = \ln(\mu_i)</math>. | |||
Damit Lösungen der Bewegungsgleichung stabil sind, muss | |||
::<math>|\mu_i| < 1 \text{ bzw. } \Re(\varrho_i) < 0</math> | |||
für alle Eigenwerte gelten. Die Fudnamentalmatrix erhalten wir am besten durch die numerische Lösung der Bewegungsgleichung als Anfangswertproblem - hier mit dem [[Anfangswertprobleme/Methoden zur Lösung von Anfangswertproblemen/Runge-Kutta-Verfahren 4.ter Ordnung|Runge-Kutta-Verfahren 4.ter Ordnung]] - z.B. für | |||
::<math>\Lambda = 1, \;\; \Gamma = 1.</math> | |||
Durch zweifache Lösung des Anfangswertproblems finden wir | |||
::<math>\underline{\underline{\Phi}}^* = \begin{pmatrix}0.024 &1.168\\ 1.168 &15.035\end{pmatrix}</math>. | |||
Die Fundamentalmatrix hat die Eigenwerte | |||
::<math>\begin{array}{l} \mu_1 = -0.0661,\\\mu_2 = 15.1256\end{array}</math> | |||
und besitzt damit einen Eigenwert, dessen Betrag größer als "1" ist - die Lösung ist instabil. [[Datei:Kw30-21.png|mini|Instabile Lösung|alternativtext=|links]]<br clear="all"/> | |||
Das können wir prüfen, indem wir uns die numerische Lösung im Zeitbereich anschauen: | |||
* der Winkel der Auslenkung wächst (exponentiell) mit der Zeit. | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
/*********************************************************/ | |||
/* numerical solution of IVP */ | |||
numpars: [Lambda = [-1,2], Gamma = [0,3]]; | |||
times : subst([t0 = 0, tmax = 1, dt = 0.01], | |||
[t, t0, tmax, dt]); | |||
runs : [30,30]; | |||
stateVabs : [p,v]; | |||
initiVals : [[0,1],[1,0]]; | |||
for p1: 0 thru runs[1] do | |||
(for p2: 0 thru runs[2] do | |||
(print("step ",p1," - ", p2), | |||
pars: [Lambda = subst(numpars, Lambda)[1]+(subst(numpars, Lambda)[2]-subst(numpars, Lambda)[1])*p1/runs[1], | |||
Gamma = subst(numpars, Gamma )[1]+(subst(numpars, Gamma )[2]-subst(numpars, Gamma )[1])*p2/runs[2]], | |||
dgl1stOrder : float(subst(pars,[rhs(eom[1]),rhs(eom[2])])), | |||
Phi : [], | |||
for i:1 thru 2 do | |||
(ivs : rk(dgl1stOrder, stateVabs, initiVals[i], times), | |||
Phi : append(Phi,[rest (ivs[length(ivs)], 1)])), | |||
Phi : funmake('matrix,Phi), | |||
mu[p1+1,p2+1] : lmax(abs(float(eigenvalues(Phi)[1])))))$ | |||
</syntaxhighlight> | |||
}} | |||
<!--------------------------------------------------------------------------------> | |||
===Ince-Struttsche Karte=== | |||
Diese Untersuchung können wir nun für eine Reihe von Parameter-Konstellationen wiederholen und den größeren der beiden charakteristischen Exponenten jeweils auftragen. | |||
[[Datei:Kw30-22.png|mini|Stabilitätskarte|alternativtext=|200x200px]]Wir untersuchen den Bereich | |||
::<math>\Lambda = -1 \ldots 2, \;\; \Gamma = 0 \ldots 3.</math> | |||
und tragen die Werte des Exponenten ''ρ'' farbig kodiert auf: | |||
Bei genauerer Analyse können wir die stabilen (grün) von den instabilen Parameter-Bereichen durch eine rote Linie trennen. | |||
Dies ist ein Ausschnitt der Ince-Struttschen Karte. Sie gibt die Stabilität der Lösungen der Mathieuschen Differentialgleichungen an.[[Datei:Kw30-23.png|mini|Ince-Struttsche Karte|alternativtext=|links]] | |||
Und so sieht die gesamte Ince-Struttsche Karte aus: | |||
Achtung: hier wurden unterschiedliche Parameterwerte für ''Λ'' und ''Γ'' verwendet! | |||
Wir erkennen: bei periodischer Erregung des Fußpunktes hat | |||
* das gewöhnliche mathematische Pendel (''Λ>0'') große Bereiche dynamischer Instabilität! | |||
* das inverse Pendel (''Λ<0'') Bereiche dynamischer Stabilität! | |||
<hr/> | |||
'''Links''' | |||
* [https://youtu.be/rwGAzy0noU0 Inverted pendulum with a vertically oscillated pivot.] | |||
'''Literature''' | |||
* ... | |||
Aktuelle Version vom 23. November 2022, 08:12 Uhr
Aufgabenstellung
Manchmal stößt man in unscheinbaren Aufgabenstellungen auf unerwartete Hindernisse - so in dieser Aufgabe eines mathematischen Pendels, die auf eine Bewegungsgleichung mit periodischen Koeffizienten führt.
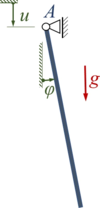
Das Pendel der Masse m und Länge ℓ der Aufgabe hat einen in A senkrecht mit u(t) periodisch bewegten Aufhängepunkt.
Berechnen Sie die Stabilität der Lösung der linearisierten Bewegungsgleichung für verschiedene Parameterkombinationen.
Gegeben sind
- m, ℓ, g sowie
Lösung mit Maxima
Equations of Motion
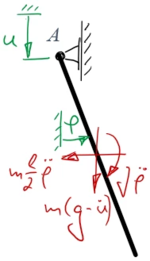
Aus dem Freikörperbild erhalten wir die Bewegungsgleichung
mit
- .
Wir linearisieren und erhalten mit
die lineare Differentialgleichung mit perdiodischen Koeffizienten
- .
Das ist eine Grundform der Mathieuschen Differentialgleichung - die wir noch in dimensionslose Form bringen wollen. Dazu soll die zugeordnete gewöhnliche Differentialgleichung mit konstanten Koeffizienten, also für
- ,
in dimensionsloser Schreibweise und für einfache Parameter-Konstellationen die Periodendauer "1" haben. Das erreichen mit der dimensionslosen Zeit
und den dimensionslosen Parametern
- .
Damit ist
- .
Für Λ=1 ist das wie gewünscht eine Bewegungsgleichung mit der Periodendauer "1":
- .
/*********************************************************/
/* MAXIMA script */
/* version: wxMaxima 15.08.2 */
/* author: Andreas Baumgart */
/* last updated: 2018-12-30 */
/* ref: Kw30 */
/* description: finds the solution for */
/* Mathieus Differential Equation */
/*********************************************************/
/*********************************************************/
declare("ℓ", alphabetic);
load(eigen)$
/*load (lapack)$*/
/* declare parameters */
params: [J=m*ℓ^2/12, Omega=2*%pi/T, Lambda = (3*g)/(Omega^2*ℓ), Gamma = (3*U)/ℓ];
/*********************************************************/
/* equations of motion */
eom: J*'diff(phi,t,2) + ℓ/2*m*ℓ/2*'diff(phi,t,2)*cos(phi) + m*(g-'diff(u,t,2))*ℓ*sin(phi) = 0;
linearize : [sin(phi) = phi, cos(phi) = 1];
eom : subst(params,subst(linearize,eom));
eom : subst(['diff(phi,t,2) = 'diff(p,tau,2)/T^2,subst(params,'diff(u,t,2) = diff(U*cos(Omega*t),t,2)), t=T*tau],eom);
eom : expand(subst(solve(rest(params, 1),[T,g,U]),eom*12*%pi^2/m/ℓ^2/Omega^2));
eom : ['diff(p,t) = v,
'diff(v,t) = subst([phi=p,tau=t],subst(solve(eom, 'diff(p,tau,2))[1],'diff(p,tau,2)))];
Solve and Check for Stability of Solution
Für die Stabilität der Bewegungsgleichung brauchen wir den Satz von Floquet-Ljapunow und die Fundamentalmatrix Φ. Zunächst schreiben wir die Bewegungsgleichung als Differentialgleichung erster Ordnung als
bzw. als
- .
Durch den Zeit-periodischen Koeffizienten in τ hat diese Bewegungsgleichung keine "einfachen" Lösungen der Form eλt mehr. Statt dessen untersuchen wir die Stabilität anhand der Fundamentalmatrix Φ*, in der zwei Fundamentalösungen
mit
und
stehen.
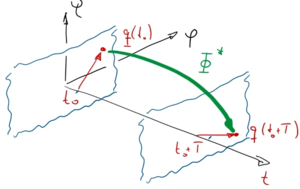
Wir interpretieren also die Fundamentalmatrix Φ* als Abbildungsvorschrift, um die Anfangsbedingungen q(0) über das Zeitintervall - hier T = 1 - hinweg abzubilden.
Die Eigenwerte μi der Fundamentalmatrix heißen
- charakteristische Multiplikatoren.
Die charakteristischen Exponenten sind
- .
Damit Lösungen der Bewegungsgleichung stabil sind, muss
für alle Eigenwerte gelten. Die Fudnamentalmatrix erhalten wir am besten durch die numerische Lösung der Bewegungsgleichung als Anfangswertproblem - hier mit dem Runge-Kutta-Verfahren 4.ter Ordnung - z.B. für
Durch zweifache Lösung des Anfangswertproblems finden wir
- .
Die Fundamentalmatrix hat die Eigenwerte
und besitzt damit einen Eigenwert, dessen Betrag größer als "1" ist - die Lösung ist instabil.
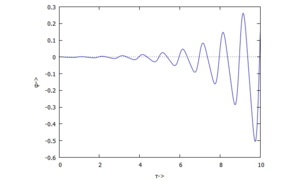
Das können wir prüfen, indem wir uns die numerische Lösung im Zeitbereich anschauen:
- der Winkel der Auslenkung wächst (exponentiell) mit der Zeit.
/*********************************************************/
/* numerical solution of IVP */
numpars: [Lambda = [-1,2], Gamma = [0,3]];
times : subst([t0 = 0, tmax = 1, dt = 0.01],
[t, t0, tmax, dt]);
runs : [30,30];
stateVabs : [p,v];
initiVals : [[0,1],[1,0]];
for p1: 0 thru runs[1] do
(for p2: 0 thru runs[2] do
(print("step ",p1," - ", p2),
pars: [Lambda = subst(numpars, Lambda)[1]+(subst(numpars, Lambda)[2]-subst(numpars, Lambda)[1])*p1/runs[1],
Gamma = subst(numpars, Gamma )[1]+(subst(numpars, Gamma )[2]-subst(numpars, Gamma )[1])*p2/runs[2]],
dgl1stOrder : float(subst(pars,[rhs(eom[1]),rhs(eom[2])])),
Phi : [],
for i:1 thru 2 do
(ivs : rk(dgl1stOrder, stateVabs, initiVals[i], times),
Phi : append(Phi,[rest (ivs[length(ivs)], 1)])),
Phi : funmake('matrix,Phi),
mu[p1+1,p2+1] : lmax(abs(float(eigenvalues(Phi)[1])))))$
Ince-Struttsche Karte
Diese Untersuchung können wir nun für eine Reihe von Parameter-Konstellationen wiederholen und den größeren der beiden charakteristischen Exponenten jeweils auftragen.
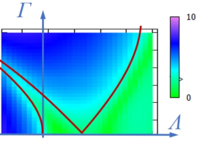
Wir untersuchen den Bereich
und tragen die Werte des Exponenten ρ farbig kodiert auf:
Bei genauerer Analyse können wir die stabilen (grün) von den instabilen Parameter-Bereichen durch eine rote Linie trennen.
Dies ist ein Ausschnitt der Ince-Struttschen Karte. Sie gibt die Stabilität der Lösungen der Mathieuschen Differentialgleichungen an.
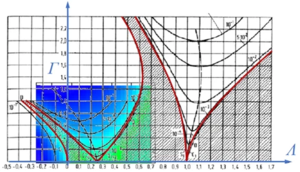
Und so sieht die gesamte Ince-Struttsche Karte aus:
Achtung: hier wurden unterschiedliche Parameterwerte für Λ und Γ verwendet!
Wir erkennen: bei periodischer Erregung des Fußpunktes hat
- das gewöhnliche mathematische Pendel (Λ>0) große Bereiche dynamischer Instabilität!
- das inverse Pendel (Λ<0) Bereiche dynamischer Stabilität!
Links
Literature
- ...