Gelöste Aufgaben/DGEC: Unterschied zwischen den Versionen
Die Seite wurde neu angelegt: „tra“ |
Keine Bearbeitungszusammenfassung |
||
| (15 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
[[Category:Gelöste_Aufgaben]] | |||
[[Category:Randwertproblem]] | |||
[[Category:Timoshenko-Balken]] | |||
[[Category:Euler-Bernoulli-Balken]] | |||
[[Category:Maxima]] | |||
==Aufgabenstellung== | |||
Wie sich die Balkenmodell von Euler-Bernoulli und Timoshenko in Ihrem Modellverhalten unterscheiden, untersuchen wir hier. | |||
<onlyinclude> | |||
[[Datei:DGEC-01.png|mini|200x200px|Lageplan|alternativtext=|links]] | |||
Ein Balken ''AB'' (Länge ''ℓ'', Rechteck-Querschnitt ''h*b'', Elastizitäts-Module ''E'') ist in ''A'' fest eingespannt und in ''B'' durch eine Parallelführung gelagert. | |||
In ''B'' wird er durch eine senkrechte Kraft ''F'' belastet. | |||
Wir vergleichen die Auslenkung in ''B'' nach den Balken-Modellen von | |||
*[[Sources/Lexikon/Euler-Bernoulli-Balken|Euler-Bernoulli]] und | |||
*[[Sources/Lexikon/Timoshenko-Balken|Timoshenko]] | |||
</onlyinclude> | |||
Der Balken-Querschnitt sei rechteckig mit den Abmessungen ''h'', ''b'': | |||
[[Datei:DGEC-02.png|alternativtext=|rahmenlos|67x67px]] | |||
Hier gelte für den Querschnitt ''h=b''. | |||
==Lösung mit Maxima== | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Header | |||
|text=Wir suchen Näherungslösungen für die Verschiebung des Punktes ''B'' mit dem [[Werkzeuge/Gleichgewichtsbedingungen/Arbeitsprinzipe der Analytischen Mechanik/Prinzip der virtuellen Verrückungen|Prinzip der virtuellen Verrückungen]] auf Basis der Bewegungsgleichungen aus [[Gelöste_Aufgaben/DGEB|DGEB]]. Dazu setzen wir einmal die Verschiebung und Verdrehung der Querschnitte jeweils nach dem Modell des | |||
*Timoshenko-Balkens und | |||
*Euler-Bernoulli-Balkens | |||
an. | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
/*******************************************************/ | |||
/* MAXIMA script */ | |||
/* version: wxMaxima 15.08.2 */ | |||
/* author: Andreas Baumgart */ | |||
/* last updated: 2018-12-09 */ | |||
/* ref: Euler-Bernoulli Beam */ | |||
/* description: derives the equations of motion for */ | |||
/* the Timoshenko and EBB beam */ | |||
/*******************************************************/ | |||
/* declare variational variables */ | |||
declare("δW", alphabetic); /* virtual work */ | |||
declare("δA", alphabetic); /* virtual work of implied external forces */ | |||
declare("δΠ", alphabetic); /* virtual strain energy */ | |||
declare("δw", alphabetic); | |||
declare( "ϕ", alphabetic); | |||
declare("δϕ", alphabetic); | |||
declare( "Φ", alphabetic); | |||
declare("δΦ", alphabetic); | |||
declare( "ℓ", alphabetic); | |||
</syntaxhighlight> | |||
}} | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Parameter | |||
|text=Parameter sind | |||
::<math>\displaystyle G=\frac{E}{2 \left( \nu+1\right) },\nu=\frac{3}{10},A={{h}^{2}},I=\frac{{{h}^{4}}}{12}</math> | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
/*******************************************************/ | |||
/* parameters */ | |||
params: [GA=G*A, EI = E*I, G = E/(2*(1+nu)), nu=3/10, A=h^2, I=h^4/12]; | |||
</syntaxhighlight> | |||
}} | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Trial-Functions | |||
|text= | |||
Wir wählen als [[Sources/Lexikon/Trial-Function|Trial-Functions]] für die Auslenkung ''w'' und die Verdrehung ''ϕ'' des Timoshenko-Balkens: | |||
::<math>\begin{array}{ll}w(x) &= W \cdot (3\,\xi^2-2\,\xi^3),\\ \phi(x) &= \Phi\cdot 4\,\xi\,(1-\xi) \end{array}</math> . | |||
Beim Euler-Bernoulli-Balken ist | |||
::<math>\phi(x) = w')(x)</math> | |||
fest "eingebaut" - wir brauchen keine Trial-Funktion für ''ϕ''. | |||
Und so sehen die beiden Trial-Funtions aus: | |||
[[Datei:DGEC-Trialfcts.png|mini|Unsere Trialfunctions.]] | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
/*******************************************************/ | |||
/* trial functions */ | |||
trials : [w = W*(3*xi^2-2*xi^3), ϕ = Φ*4*xi*(1-xi)]; | |||
plot2d(subst(trials,[w/W, ϕ/Φ]), [xi,0,1], [xlabel, "ξ ->"], [ylabel, "φ ->"]); | |||
</syntaxhighlight> | |||
}} | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Equilibrium-Conditions | |||
|text= | |||
Mit dem Prinzip der virtuellen Verrückungen lautet die Gleichgewichtsbedingung | |||
::<math>\begin{array}{ll}\delta W &= \delta W^a - \delta \Pi\\&\stackrel{!}{=}0\end{array}</math>. | |||
Aus DGEB wissen wir für die [[Sources/Lexikon/Virtuelle Formänderungsenergie|Virtuelle Formänderungsenergie]] | |||
<table> | |||
<tr><th>... für den Timoshenko-Balken</th><th>... für den Euler-Bernoulli-Balken</th></tr> | |||
<tr><td><math>\begin{array}{lcl} \delta\Pi = &\displaystyle \int_0^\ell& \displaystyle \frac{1}{4} G\,A\,(w'-\phi)\cdot (\delta w'-\delta \phi) \\&+ &E\,I\,\phi'\,\delta \phi' \; dx \end{array}</math></td><td><math>\displaystyle \delta\Pi = \int_0^\ell EI\,w''\,\delta w'' \; dx</math></td></tr> | |||
</table> | |||
Und die virtuelle Arbeit der äußeren Kraft ''F'' ist | |||
::<math>\delta W^a = F\;\delta W</math> | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
/*******************************************************/ | |||
/* Principle of Virtual Work */ | |||
δΠ : [ 1/4*GA*('diff(w,x)-ϕ)*'diff(δw,x) | |||
+ 1/4*GA*(ϕ-'diff(w,x))* δϕ | |||
+ EI*'diff(ϕ,x)*'diff(δϕ,x), | |||
EI*'diff(w,x,2)*'diff(δw,x,2)]; | |||
δA : F*δW; | |||
Q : [[ W, Φ, w, ϕ], | |||
[δW,δΦ,δw,δϕ]]; | |||
varia : makelist(Q[1][i]=Q[2][i],i,1,4); | |||
δΠ : subst([xi=x/ℓ],subst(trials,subst(subst(varia,trials),δΠ))); | |||
δΠ : integrate(ev(δΠ,nouns),x,0,ℓ); | |||
</syntaxhighlight> | |||
}} | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Solving | |||
|text= | |||
Aus den Gleichgewichtsbedingungen erhalten wir die Gleichungen von | |||
*''W'' und ''Φ'' für den Timoshenko-Balken und | |||
*''W'' für den Euler-Bernoulli-Balken. | |||
<table cellpadding="10px"> | |||
<tr><th>Timoshenko</th><th>Euler-Bernoulli</th></tr> | |||
<tr><td><math>\begin{array}{ll}\displaystyle \frac{3 \, G A}{10 \, \ell} \cdot W-\frac{G A}{5} \cdot \Phi &=F,\\ | |||
\displaystyle \left(\frac{2\, G A\, \ell}{15}+\frac{16\, E I}{3 \ell}\right) \cdot \Phi -\frac{G A}{5}\cdot W&=0 | |||
\end{array}</math> | |||
</td><td><math>\displaystyle \frac{12 \, E I}{{{\ell}^{3}}}\, W=F</math></td></tr> | |||
<tr><td colspan="2">mit der Lösung></td></tr> | |||
<tr><td><math>\displaystyle W=\frac{G A\, {{\ell}^{3}}+40 \,E I\,\ell}{12\,E I\,G A}\,F,\;\;\Phi =\frac{{{\ell}^{2}}}{8\,E I}\,F</math></td><td><math>\displaystyle W=\frac{{{\ell}^{3}}}{12\,E I}\,F</math></td></tr> | |||
</table> | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
/*******************************************************/ | |||
/* equations of motion */ | |||
eom: [makelist(coeff(expand(δΠ[1]-δA),Q[2][i])=0,i,1,2), | |||
coeff(expand(δΠ[2]-δA),Q[2][1])=0]; | |||
sol: [solve(eom[1],[ W, Φ])[1], solve(eom[2], W)]; | |||
</syntaxhighlight> | |||
}} | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Post-Processing | |||
|text= | |||
Einsetzen der Parameter liefert die Verschiebung des Punkte | |||
::<math>\displaystyle \tilde{W} = \frac{W}{\displaystyle \frac{\ell^3\,F}{E\,h^4}} \text{ für } \alpha = \frac{h}{\ell}:</math>: | |||
Wir sehen: für schlanke Balken bis α<0.2 können wir getrost mit der Euler-Bernoulli-Hypothese arbeiten - für "stäbigere" Balken brauchen wir mindestens das Timoshenko-Modell. | |||
[[Datei:DGEC-Ergebnis.png|mini|Vergleich von Timoshenko und Euler-Bernoulli-Modell.]] | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
/*******************************************************/ | |||
/* post-processing */ | |||
sol: ratsimp(subst([h=alpha*ℓ],subst(params,sol/(F*ℓ^3/(E*h^4))))); | |||
plot2d([rhs(sol[1][1]),rhs(sol[2][1])], [alpha,0.0001,0.5], [y,0,3], logx, [xlabel, "α ->"], [ylabel, "W/(Fℓ^3/12EI) ->"], [legend,"Timoshenko","Euler-Bernoulli"]); | |||
</syntaxhighlight> | |||
}} | |||
'''Links''' | |||
*... | |||
'''Literature''' | |||
*... | |||
Aktuelle Version vom 29. März 2021, 06:27 Uhr
Aufgabenstellung
Wie sich die Balkenmodell von Euler-Bernoulli und Timoshenko in Ihrem Modellverhalten unterscheiden, untersuchen wir hier.
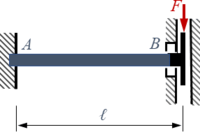
Ein Balken AB (Länge ℓ, Rechteck-Querschnitt h*b, Elastizitäts-Module E) ist in A fest eingespannt und in B durch eine Parallelführung gelagert.
In B wird er durch eine senkrechte Kraft F belastet.
Wir vergleichen die Auslenkung in B nach den Balken-Modellen von
Der Balken-Querschnitt sei rechteckig mit den Abmessungen h, b:
Hier gelte für den Querschnitt h=b.
Lösung mit Maxima
Header
Wir suchen Näherungslösungen für die Verschiebung des Punktes B mit dem Prinzip der virtuellen Verrückungen auf Basis der Bewegungsgleichungen aus DGEB. Dazu setzen wir einmal die Verschiebung und Verdrehung der Querschnitte jeweils nach dem Modell des
- Timoshenko-Balkens und
- Euler-Bernoulli-Balkens
an.
/*******************************************************/
/* MAXIMA script */
/* version: wxMaxima 15.08.2 */
/* author: Andreas Baumgart */
/* last updated: 2018-12-09 */
/* ref: Euler-Bernoulli Beam */
/* description: derives the equations of motion for */
/* the Timoshenko and EBB beam */
/*******************************************************/
/* declare variational variables */
declare("δW", alphabetic); /* virtual work */
declare("δA", alphabetic); /* virtual work of implied external forces */
declare("δΠ", alphabetic); /* virtual strain energy */
declare("δw", alphabetic);
declare( "ϕ", alphabetic);
declare("δϕ", alphabetic);
declare( "Φ", alphabetic);
declare("δΦ", alphabetic);
declare( "ℓ", alphabetic);
Parameter
Parameter sind
/*******************************************************/
/* parameters */
params: [GA=G*A, EI = E*I, G = E/(2*(1+nu)), nu=3/10, A=h^2, I=h^4/12];
Trial-Functions
Wir wählen als Trial-Functions für die Auslenkung w und die Verdrehung ϕ des Timoshenko-Balkens:
- .
Beim Euler-Bernoulli-Balken ist
fest "eingebaut" - wir brauchen keine Trial-Funktion für ϕ.
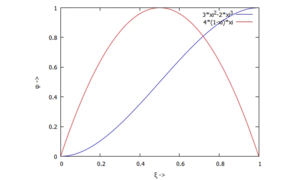
Und so sehen die beiden Trial-Funtions aus:
/*******************************************************/
/* trial functions */
trials : [w = W*(3*xi^2-2*xi^3), ϕ = Φ*4*xi*(1-xi)];
plot2d(subst(trials,[w/W, ϕ/Φ]), [xi,0,1], [xlabel, "ξ ->"], [ylabel, "φ ->"]);
Equilibrium-Conditions
Mit dem Prinzip der virtuellen Verrückungen lautet die Gleichgewichtsbedingung
- .
Aus DGEB wissen wir für die Virtuelle Formänderungsenergie
| ... für den Timoshenko-Balken | ... für den Euler-Bernoulli-Balken |
|---|---|
Und die virtuelle Arbeit der äußeren Kraft F ist
/*******************************************************/
/* Principle of Virtual Work */
δΠ : [ 1/4*GA*('diff(w,x)-ϕ)*'diff(δw,x)
+ 1/4*GA*(ϕ-'diff(w,x))* δϕ
+ EI*'diff(ϕ,x)*'diff(δϕ,x),
EI*'diff(w,x,2)*'diff(δw,x,2)];
δA : F*δW;
Q : [[ W, Φ, w, ϕ],
[δW,δΦ,δw,δϕ]];
varia : makelist(Q[1][i]=Q[2][i],i,1,4);
δΠ : subst([xi=x/ℓ],subst(trials,subst(subst(varia,trials),δΠ)));
δΠ : integrate(ev(δΠ,nouns),x,0,ℓ);
Solving
Aus den Gleichgewichtsbedingungen erhalten wir die Gleichungen von
- W und Φ für den Timoshenko-Balken und
- W für den Euler-Bernoulli-Balken.
| Timoshenko | Euler-Bernoulli |
|---|---|
| mit der Lösung> | |
/*******************************************************/
/* equations of motion */
eom: [makelist(coeff(expand(δΠ[1]-δA),Q[2][i])=0,i,1,2),
coeff(expand(δΠ[2]-δA),Q[2][1])=0];
sol: [solve(eom[1],[ W, Φ])[1], solve(eom[2], W)];
Post-Processing
Einsetzen der Parameter liefert die Verschiebung des Punkte
- :
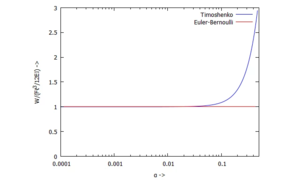
Wir sehen: für schlanke Balken bis α<0.2 können wir getrost mit der Euler-Bernoulli-Hypothese arbeiten - für "stäbigere" Balken brauchen wir mindestens das Timoshenko-Modell.
/*******************************************************/
/* post-processing */
sol: ratsimp(subst([h=alpha*ℓ],subst(params,sol/(F*ℓ^3/(E*h^4)))));
plot2d([rhs(sol[1][1]),rhs(sol[2][1])], [alpha,0.0001,0.5], [y,0,3], logx, [xlabel, "α ->"], [ylabel, "W/(Fℓ^3/12EI) ->"], [legend,"Timoshenko","Euler-Bernoulli"]);
Links
- ...
Literature
- ...