Gelöste Aufgaben/FEB4: Unterschied zwischen den Versionen
KKeine Bearbeitungszusammenfassung |
|||
| (16 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 13: | Zeile 13: | ||
<onlyinclude> | <onlyinclude> | ||
[[Datei:FEB4-01.png|mini|235x235px|Lageplan]] | [[Datei:FEB4-01.png|left|mini|235x235px|Lageplan]] | ||
Das skizzierte System besteht aus [[Sources/Lexikon/Euler-Bernoulli-Balken|Euler-Bernoulli-Balken]] (jeweils Länge ''a'') der Biegesteifigkeit ''EI''. Die Konstruktion wird in ''A'' durch ein gelenkiges Festlager gehalten und in ''B'' durch die Kraft ''F'' belastet. | Das skizzierte System besteht aus [[Sources/Lexikon/Euler-Bernoulli-Balken|Euler-Bernoulli-Balken]] (jeweils Länge ''a'') der Biegesteifigkeit ''EI''. Die Konstruktion wird in ''A'' durch ein gelenkiges Festlager gehalten und in ''B'' durch die Kraft ''F'' belastet. | ||
| Zeile 23: | Zeile 23: | ||
== Lösung mit Maxima == | == Lösung mit Maxima == | ||
<!-------------------------------------------------------------------------------->{{MyCodeBlock|title=Header | |||
<!--------------------------------------------------------------------------------> | |text= | ||
Für das FE-Modell wollen wir nicht alle Sektionen der Feder modellieren - wir schneiden die Feder entlang ihrer Längsachse durch und nehmen eins der so entstandenen Elemente exemplarisch heraus.[[Datei:FEB4-11.png|mini|175x175px|Federelement.]]Von diesen Elementen haben wir fünf in der Feder - die Längung dieses Elements der Feder entspricht also 1/5 der Feder-Längung in ''B''. | Für das FE-Modell wollen wir nicht alle Sektionen der Feder modellieren - wir schneiden die Feder entlang ihrer Längsachse durch und nehmen eins der so entstandenen Elemente exemplarisch heraus.[[Datei:FEB4-11.png|mini|175x175px|Federelement.]]Von diesen Elementen haben wir fünf in der Feder - die Längung dieses Elements der Feder entspricht also 1/5 der Feder-Längung in ''B''. | ||
| Zeile 32: | Zeile 31: | ||
Aber Achtung: so wie gezeichnet ist es statisch unbestimmt: wir können im Gleichgewicht beliebige Verschiebungen des Systems in Feder-Längsrichtung angeben. | Aber Achtung: so wie gezeichnet ist es statisch unbestimmt: wir können im Gleichgewicht beliebige Verschiebungen des Systems in Feder-Längsrichtung angeben. | ||
{{MyTip|title=Geht's noch einfacher?|text= | |||
Geht's noch einfacher? | |||
* Wie müsste ein System aussehen, das noch einfacher gestrickt ist? | * Wie müsste ein System aussehen, das noch einfacher gestrickt ist? | ||
* Welche neuen Randbedingungen ergeben sich? | * Welche neuen Randbedingungen ergeben sich? | ||
}} | |||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
/*******************************************************/ | |||
/* MAXIMA script */ | |||
/* version: wxMaxima 16.04.2 */ | |||
/* author: Andreas Baumgart */ | |||
/* last updated: 2020-01-10 */ | |||
/* ref: TM-C */ | |||
/* description: FEM-solution for spring section */ | |||
/*******************************************************/ | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
<!-------------------------------------------------------------------------------->Wir haben also ein Ersatz-System mit drei Finiten Elementen und vier Knoten:[[Datei:FEB4-12.png|mini|336x336px|Knoten und Stäbe.]] | <!-------------------------------------------------------------------------------->{{MyCodeBlock|title=Declarations | ||
|text= | |||
Wir haben also ein Ersatz-System mit drei Finiten Elementen und vier Knoten:[[Datei:FEB4-12.png|mini|336x336px|Knoten und Stäbe.]] | |||
Die Knoten 0 und 3 entstehen in unserem Ersatz-System, weil hier das Biegemoment in den horizontalen Sektionen (I und III) Null ist. Diese beiden Sektionen sind nur ''a/2'' lang, die vertikale Sektion ist ''a'' lang. | Die Knoten 0 und 3 entstehen in unserem Ersatz-System, weil hier das Biegemoment in den horizontalen Sektionen (I und III) Null ist. Diese beiden Sektionen sind nur ''a/2'' lang, die vertikale Sektion ist ''a'' lang. | ||
| Zeile 53: | Zeile 58: | ||
Dementsprechnd haben die drei Finiten Elementen die Längen | Dementsprechnd haben die drei Finiten Elementen die Längen | ||
<math>\begin{array}{l} | ::<math>\begin{array}{l} | ||
\ell_1 = a/2\\ | \ell_1 = a/2\\ | ||
\ell_2 = a\\ | \ell_2 = a\\ | ||
| Zeile 59: | Zeile 64: | ||
\end{array}</math> . | \end{array}</math> . | ||
Die Element-Steifigkeitsmatrix kopieren wir aus Abschnitt FEM-Formulierung für den Euler-Bernoulli-Balken zu: | Die Element-Steifigkeitsmatrix kopieren wir aus Abschnitt [[Sources/Anleitungen/FEM-Formulierung für den Euler-Bernoulli-Balken|FEM-Formulierung für den Euler-Bernoulli-Balken]] zu: | ||
<math>\displaystyle K_i(\ell_i) = \frac{E I}{\ell_i^3}\cdot \begin{pmatrix}12 & 6\cdot \ell & -12 & 6\cdot \ell_i\\ | ::<math>\displaystyle K_i(\ell_i) = \frac{E I}{\ell_i^3}\cdot \begin{pmatrix}12 & 6\cdot \ell & -12 & 6\cdot \ell_i\\ | ||
6\cdot \ell_i & 4\cdot {{\ell_i}^{2}} & -6\cdot \ell_i & 2\cdot {{\ell_i}^{2}}\\ | 6\cdot \ell_i & 4\cdot {{\ell_i}^{2}} & -6\cdot \ell_i & 2\cdot {{\ell_i}^{2}}\\ | ||
-12 & -6\cdot \ell_i & 12 & -6\cdot \ell_i\\ | -12 & -6\cdot \ell_i & 12 & -6\cdot \ell_i\\ | ||
6\cdot \ell_i & 2\cdot {{\ell_i}^{2}} & -6\cdot \ell_i & 4\cdot {{\ell_i}^{2}}\end{pmatrix}</math> . | 6\cdot \ell_i & 2\cdot {{\ell_i}^{2}} & -6\cdot \ell_i & 4\cdot {{\ell_i}^{2}}\end{pmatrix}</math> . | ||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
1 | |||
/*******************************************************/ | |||
/* coordinates and boundary conditions */ | |||
l : [a/2,a,a/2]; | |||
norm : ŵ = F*a^3/(3*EI) * 5; | |||
X : append(makelist(Q[i]= [W[i-1], Φ[i-1], W[i], Φ[i]],i,1,3),[Q[0]= [U[1], Ψ[1], Ψ[2], U[3]]]); | |||
δX : subst([Q=δQ,W=δW,Φ=δΦ],X); | |||
/* boundary conditions */ | |||
kinematics: [[W[0]= 0 , δW[0]= 0 ], | |||
[W[1]= 0 , W[2]=0,δW[1]= 0 ,δW[2]=0], | |||
[W[2]=-W[1], δW[2]=-δW[1] ]]; | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
<!-------------------------------------------------------------------------------->{{MyCodeBlock|title=Coordinates | |||
|text= | |||
Für jedes Finite Element führen wir zuerst das standardisierte lokale ''x/z''-[[Sources/Lexikon/Koordinaten|Koordinatensystem]][[Datei:Link.png|rahmenlos]] ein. Und wir definieren neue, anschauliche - globale - Koordinaten des Systems, um sie von den Standard-Koordinaten ''W<sub>i</sub> , Φ<sub>i</sub>'' unterscheiden zu können: | Für jedes Finite Element führen wir zuerst das standardisierte lokale ''x/z''-[[Sources/Lexikon/Koordinaten|Koordinatensystem]][[Datei:Link.png|rahmenlos]] ein. Und wir definieren neue, anschauliche - globale - Koordinaten des Systems, um sie von den Standard-Koordinaten ''W<sub>i</sub> , Φ<sub>i</sub>'' unterscheiden zu können: | ||
<table style="background-color:#FFFFFF;" class="wikitable"> | |||
<tr><th>Lokale Orts-Koordinaten ''x<sub>i</sub>, z<sub>i</sub>''</th><th>Globale Knoten-Koordinaten ''U<sub>i</sub>, Ψ<sub>i</sub>''</th></tr> | |||
<tr><td>[[Datei:FEB4-14.png|alternativtext=|rahmenlos|336x336px]]</td> | |||
<td>[[Datei:FEB4-15.png|alternativtext=|rahmenlos|284x284px]]</td></tr> | |||
</table> | |||
Wir haben also je Element die eingezeichneten globalen Knoten-Koordinaten | Wir haben also je Element die eingezeichneten globalen Knoten-Koordinaten | ||
<math>U_{i-1},\Psi_{i-1}, U_{i}, \Psi_{i}</math> | ::<math>U_{i-1},\Psi_{i-1}, U_{i}, \Psi_{i}</math> | ||
sowie die lokalen FE-Koordinaten | sowie die lokalen FE-Koordinaten | ||
<math>W_{i-1},\Phi_{i-1},W_{i},\Phi_{i}</math>. | ::<math>W_{i-1},\Phi_{i-1},W_{i},\Phi_{i}</math>. | ||
die wir miteinander "verheiraten" müssen. Das machen wir beim Komponieren des Gesamt-Gleichungssystems. | die wir miteinander "verheiraten" müssen. Das machen wir beim Komponieren des Gesamt-Gleichungssystems. | ||
| Zeile 94: | Zeile 109: | ||
Die virtuelle Formänderungsenergie eines Finiten Elements ist nun | Die virtuelle Formänderungsenergie eines Finiten Elements ist nun | ||
<math>\delta \Pi_i = \left( W_{i-1} ,\Phi_{i-1}, W_{i} ,\Phi_{i}\right)^T \cdot \underline{\underline{K}}_i(\ell_i) \cdot \left(\begin{array}{c}W_{i-1}\\\Phi_{i-1}\\W_{i}\\\Phi_{i}\end{array}\right)</math>, | ::<math>\delta \Pi_i = \left( W_{i-1} ,\Phi_{i-1}, W_{i} ,\Phi_{i}\right)^T \cdot \underline{\underline{K}}_i(\ell_i) \cdot \left(\begin{array}{c}W_{i-1}\\\Phi_{i-1}\\W_{i}\\\Phi_{i}\end{array}\right)</math>, | ||
mit | mit | ||
<math>\delta \Pi = \displaystyle \sum_1^3 \delta \Pi_i </math>. | ::<math>\delta \Pi = \displaystyle \sum_1^3 \delta \Pi_i </math>. | ||
Die virtuelle Arbeit der Kraft ist dabei | Die virtuelle Arbeit der Kraft ist dabei | ||
<math>\delta W^a= F \cdot \delta U_3</math> | ::<math>\delta W^a= F \cdot \delta U_3</math> | ||
Aus den Bildern für die Knoten-Koordinaten oben lesen wir nun die (geometrischen) Rand- und Übergangsbedingungen ab und skizzieren darunter die Einarbeitung dieser Bedingungen in die virtuellen Formänderungsenergien. | Aus den Bildern für die Knoten-Koordinaten oben lesen wir nun die (geometrischen) Rand- und Übergangsbedingungen ab und skizzieren darunter die Einarbeitung dieser Bedingungen in die virtuellen Formänderungsenergien. | ||
<table style="background-color:#FFFFFF;" class="wikitable"> | |||
<tr><th>Element ''I''</th><th>Element ''II''</th><th>Element ''III''</th></tr> | |||
<tr><td><math>\begin{array}{lcl} | |||
W_0 &=&0\\ | |||
\end{array}</math></td><td><math>\begin{array}{lcl} | |||
W_1 &=&0\\ | |||
W_2 &=&0 | |||
\end{array}</math></td><td><math>\begin{array}{lcl} | |||
% | |||
\end{array}</math></td></tr> | |||
<tr><td>[[Datei:FEB4-21.png|alternativtext=|rahmenlos]]</td> | |||
<td>[[Datei:FEB4-22.png|alternativtext=|rahmenlos]]</td> | |||
<td>[[Datei:FEB4-23.png|rahmenlos]]</td></tr> | |||
</table> | |||
Dabei sind folgende Koordinaten sind in den drei Elementen gleich oder unterscheiden sich nur durch ein Vorzeichen: | Dabei sind folgende Koordinaten sind in den drei Elementen gleich oder unterscheiden sich nur durch ein Vorzeichen: | ||
<math>\begin{array}{ccccc} | ::<math>\begin{array}{ccccc} | ||
I& &II& &III\\ | I& &II& &III\\ | ||
\Phi_1&=&\Phi_1& &\\ | \Phi_1&=&\Phi_1& &\\ | ||
| Zeile 128: | Zeile 146: | ||
Was noch fehlt ist die Übersetzung der lokalen in die globalen Koordinaten | Was noch fehlt ist die Übersetzung der lokalen in die globalen Koordinaten | ||
<table style="background-color:#FFFFFF;" class="wikitable"> | |||
<tr><th>local</th><th></th><th>global</th></tr> | |||
<tr><td><math>\begin{array}{c} | |||
\Phi_0\\ | |||
W_1\\ | |||
\Phi_1\\ | |||
\Phi_2\\ | |||
W_3\\ | |||
{ | \Phi_3 | ||
\end{array}</math> | |||
</td><td> | |||
<span style="color:#800000; font-size:250%">'''↔'''</span> | |||
</td><td><math>\begin{array}{c} | |||
\Psi_0\\ | |||
U_1\\ | |||
\Psi_1\\ | |||
\Psi_2\\ | |||
U_3\\ | |||
\Psi_3 | |||
\end{array}</math></td></tr> | |||
</table> | |||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
1 | |||
/*******************************************************/ | |||
/* coordinates and boundary conditions */ | |||
l : [a/2,a,a/2]; | |||
norm : ŵ = F*a^3/(3*EI) * 5; | |||
X : append(makelist(Q[i]= [W[i-1], Φ[i-1], W[i], Φ[i]],i,1,3),[Q[0]= [U[1], Ψ[1], Ψ[2], U[3]]]); | |||
δX : subst([Q=δQ,W=δW,Φ=δΦ],X); | |||
/* boundary conditions */ | |||
kinematics: [[W[0]= 0 , δW[0]= 0 ], | |||
[W[1]= 0 , W[2]=0,δW[1]= 0 ,δW[2]=0], | |||
[W[2]=-W[1], δW[2]=-δW[1] ]]; | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
<!-------------------------------------------------------------------------------->[[Datei:FEB4-24.png|mini|253x253px|Globale Koordinaten]]{{ | <!-------------------------------------------------------------------------------->{{MyCodeBlock|title=Assembly of System Matrices | ||
|text= | |||
Wir bauen nun das Gleichungssystem | |||
zusammen, indem wir die Anteile der Element-Steifigkeitsmatrizen und die äußeren Lasten in die jeweiligen System Matrizen hineinaddieren.[[Datei:FEB4-24.png|mini|253x253px|Globale Koordinaten]]Dafür müssen wir die Koordinaten zwischen lokalen und globalen Koordinaten transformieren, nämlich | |||
::<math>\begin{array}{ccr} | |||
\Phi_0&=&\Psi_0\\ | |||
W_1&=&U_1\\ | |||
\Phi_1&=&\Psi_1\\ | |||
\Phi_2&=&-\Psi_2\\ | |||
W_3&=&-U_3\\ | |||
\Phi_3&=&-\Psi_3& | |||
\end{array}</math>. | |||
Die virtuelle Formänderungsenergie ist dann | |||
<ul> | |||
<li>für Sektion ''I'':<br/> | |||
<math>\delta\Pi_1 = \left(\delta \Psi_0, \delta U_1, \delta \Psi_1 \right) \cdot | |||
\displaystyle \frac{EI}{a^3} | |||
\begin{pmatrix}8\cdot {{a}^{2}} & -24\cdot a & 4\cdot {{a}^{2}}\\ | |||
-24\cdot a & 96 & -24\cdot a\\ | |||
4\cdot {{a}^{2}} & -24\cdot a & 8\cdot {{a}^{2}}\end{pmatrix} | |||
\cdot \left(\begin{array}{l}\Psi_0\\U_1\\\Psi_1\end{array}\right)</math></li> | |||
<li>für Sektion ''II'':<br/> | |||
<math>\delta\Pi_2 = \left(\delta \Psi_1, \delta \Psi_2 \right) \cdot | |||
\displaystyle \frac{EI}{a^3} | |||
\begin{pmatrix}4\cdot {{a}^{2}} & -2\cdot {{a}^{2}}\\ | |||
-2\cdot {{a}^{2}} & 4\cdot {{a}^{2}}\end{pmatrix} | |||
\cdot \left(\begin{array}{l}\Psi_1\\\Psi_2\end{array}\right)</math></li> | |||
<li>für Sektion III: | |||
<math>\delta\Pi_3 = \left(\delta U_1, \delta \Psi_2, \delta U_3, \delta \Psi_3 \right) \cdot | |||
\displaystyle \frac{EI}{a^3} | |||
\begin{pmatrix}96 & 24\cdot a & -96 & 24\cdot a\\ | |||
24\cdot a & 8\cdot {{a}^{2}} & -24\cdot a & 4\cdot {{a}^{2}}\\ | |||
-96 & -24\cdot a & 96 & -24\cdot a\\ | |||
24\cdot a & 4\cdot {{a}^{2}} & -24\cdot a & 8\cdot {{a}^{2}}\end{pmatrix} | |||
\cdot \left(\begin{array}{l}U_1\\\Psi_2\\U_3\\\Psi_3\end{array}\right)</math></li> | |||
</ul> | |||
Die Gesamt-Steifigkeitsmatrix aus Sektion 1 (rot) , Sektion 2 (grün) und Sektion 3 (blau) ist damit | |||
::<math>\displaystyle \underline{\underline{K}} = \frac{E\,I}{a^3} \cdot | |||
\begin{pmatrix} | |||
{\color{red}{8 a^2}} & {\color{red}{-24 a}} & {\color{red}{4 a^2}} & 0 & 0 & 0\\ | |||
{\color{red}{-24 a}} & {\color{red}{96}}+{\color{blue}{96}} & {\color{red}{-24 a}} & {\color{blue}{24 a}} & {\color{blue}{-96}} & {\color{blue}{24 a}}\\ | |||
{\color{red}{4 a^2}} & {\color{red}{-24 a}} & {\color{red}{8 a^2}}+{\color{green}{4 a^2}} & {\color{green}{-2 a^2}} & 0 & 0\\ | |||
0 & {\color{blue}{24 a}} & {\color{green}{-2 a^2}} & {\color{green}{4 a^2}}+{\color{blue}{8 a^2}} & {\color{blue}{-24 a}} & {\color{blue}{4 a^2}}\\ | |||
0 & {\color{blue}{-96}} & 0 & {\color{blue}{-24 a}} & {\color{blue}{96}} & {\color{blue}{-24 a}}\\ | |||
0 & {\color{blue}{24 a}} & 0 & {\color{blue}{4 a^2}} & {\color{blue}{-24 a}} & {\color{blue}{8 a^2}} | |||
\end{pmatrix}</math>. | |||
Die Spaltenmatrix der eingeprägten, äußeren Lasten auf das System ist dementsprechend | |||
::<math>\displaystyle \underline{P} = \left(\begin{array}{r}0\\0\\0\\0\\F\\0\end{array}\right)</math>. | |||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
1 | |||
/* system stiffness matrix K and system load matrix P */ | |||
/* assembly of system matrices */ | |||
A : [K[1]=Ki(a/2),K[2]=Ki( a ),K[3]=Ki(a/2), K[0] = zeromatrix(6,6)]; | |||
P : expand(makelist(δΠ[i] = subst(kinematics[i],transpose(subst(δX,δQ[i])).subst(A,K[i]).subst(X,Q[i])),i,1,3)); | |||
R : δW^a = F*δU[3]; | |||
/* translate to global coordinates */ | |||
globals: [ Φ[0] = Ψ[0], δΦ[0] = δΨ[0], | |||
W[1] = U[1], δW[1] = δU[1], | |||
Φ[1] = Ψ[1], δΦ[1] = δΨ[1], | |||
Φ[2] =-Ψ[2], δΦ[2] =-δΨ[2], | |||
W[3] =-U[3], δW[3] =-δU[3], | |||
Φ[3] =-Ψ[3], δΦ[3] =-δΨ[3]]; | |||
P : sum(subst(globals,P[i]),i,1,3); | |||
Y : [ Ψ[0], U[1], Ψ[1], Ψ[2], U[3], Ψ[3]]; | |||
δY : [δΨ[0], δU[1],δΨ[1],δΨ[2],δU[3],δΨ[3]]; | |||
eom : makelist(coeff(rhs(P)-rhs(R),δY[i])=0,i,1,6); | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
<!--------------------------------------------------------------------------------> | |||
<!-------------------------------------------------------------------------------->{{MyCodeBlock|title=Solving | {{MyCodeBlock|title=Solving | ||
|text= | |text= | ||
Das lineare Gleichungssystem lautet also | |||
::<math>\displaystyle \frac{E I}{a^3}\cdot | |||
\begin{pmatrix} | |||
8\cdot {{a}^{2}} & -24\cdot a & 4\cdot {{a}^{2}} & 0 & 0 & 0\\ | |||
-24\cdot a & 192 & -24\cdot a & 24\cdot a & -96 & 24\cdot a\\ | |||
4\cdot {{a}^{2}} & -24\cdot a & 12\cdot {{a}^{2}} & -2\cdot {{a}^{2}} & 0 & 0\\ | |||
0 & 24\cdot a & -2\cdot {{a}^{2}} & 12\cdot {{a}^{2}} & -24\cdot a & 4\cdot {{a}^{2}}\\ | |||
0 & -96 & 0 & -24\cdot a & 96 & -24\cdot a\\ | |||
0 & 24\cdot a & 0 & 4\cdot {{a}^{2}} & -24\cdot a & 8\cdot {{a}^{2}} | |||
\end{pmatrix} | |||
\cdot | |||
\begin{pmatrix} {{\Psi}_{0}}\\ {{U}_{1}}\\ {{\Psi}_{1}}\\ {{\Psi}_{2}}\\ {{U}_{3}}\\ {{\Psi}_{3}} \end{pmatrix} | |||
= | |||
\begin{pmatrix}0\\ 0\\ 0\\ 0\\ F\\ 0 \end{pmatrix}</math> | |||
Und dessen Lösung ist | |||
::<math>\left(\begin{array}{c} | |||
\Psi_0\\ | |||
U_1\\ | |||
\Psi_1\\ | |||
\Psi_2\\ | |||
U_3\\ | |||
\Psi_3 | |||
\end{array}\right) = | |||
\left(\begin{array}{c} | |||
\displaystyle \frac{3}{8 a}\\ | |||
\displaystyle \frac{1}{6}\\ | |||
\displaystyle \frac{1}{4 a}\\ | |||
\displaystyle \frac{1}{4 a}\\ | |||
\displaystyle \frac{1}{3}\\ | |||
\displaystyle \frac{1}{8 a} | |||
\end{array}\right)\cdot \displaystyle \frac{a^3 F}{E I}</math>. | |||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
1 | |||
/* solve ..... */ | |||
sol: solve(eom,Y)[1]; | |||
ACM : augcoefmatrix(eom, Y); | |||
ole : [K[0] = submatrix(ACM,7), p = -col(ACM,7)]; | |||
print(subst(ole, K[0]),"*",transpose(Y),"=",subst(ole,p))$ | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
<!-------------------------------------------------------------------------------->[[Datei:FEB4-25-plot.png|mini|300x300px|Verformung des Elements.]]{{ | <!-------------------------------------------------------------------------------->{{MyCodeBlock|title=Post-Processing | ||
|text= | |||
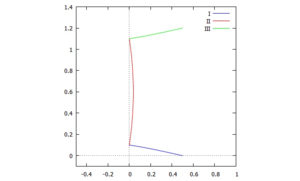
[[Datei:FEB4-25-plot.png|mini|300x300px|Verformung des Elements.]]Wir normieren die Auslenkung des Systems mit | |||
::<math>\displaystyle \hat{w} = 5 \frac{F a^3}{3 EI}</math> | |||
und plotten das System damit im ausgelenkten Zustand: | |||
Die Auslenkung in Knoten 3 ist gleichzeitig die Längung der insgesamt 5 Sub-Systeme, die Auslenkung des Gesamtsystems in B ist demnach | |||
::<math>\begin{array}{ll} | |||
u_B &= 5\cdot U_3\\ | |||
&= \displaystyle \frac{5 a^3}{3 EI} F | |||
\end{array}</math> | |||
und die gesuchte Ersatzfedersteifigkeit des Systems ist | |||
::<math>\displaystyle k = \frac{3 EI}{5 a^3}</math>. | |||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
1+1 | |||
/* post-processing */ | |||
displ: makelist(expand(subst(norm,(subst(sol,subst(globals,subst(kinematics[j],subst(X,Q[j])))).transpose(subst([ℓ[i]=l[j]],phi))/ŵ))),j,1,3); | |||
offset: subst(norm,subst(sol,U[1]/ŵ)); | |||
plot2d([[parametric, (1-t)/2, +subst([xi=t],displ[1]), [t,0,1]], | |||
[parametric, +subst([xi=t],displ[2]), offset+t, [t,0,1]], | |||
[parametric, ( t)/2, 1-subst([xi=t],displ[3]), [t,0,1]]], | |||
[x,-1/2,2/2],[y,-0.1,1.4], [same_xy , true], | |||
[legend,"I","II","III"])$ | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
| Zeile 174: | Zeile 355: | ||
'''Literature''' | '''Literature''' | ||
* ... | * ... | ||
Aktuelle Version vom 9. März 2021, 11:21 Uhr
Aufgabenstellung
Wie in FEB3 geht es hier um die Ausnutzung von Symmetrien mit einer skalaren Gleichgewichtsformulierung.
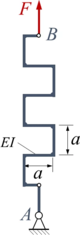
Das skizzierte System besteht aus Euler-Bernoulli-Balken (jeweils Länge a) der Biegesteifigkeit EI. Die Konstruktion wird in A durch ein gelenkiges Festlager gehalten und in B durch die Kraft F belastet.
Gesucht ist die Ersatzfeder-Steifigkeit des Systems, das Sie aus Finiten Elementen mit Euler-Bernoulli-Balken zusammensetzen.
Gesucht ist die Auslenkung des Punktes B. Das Modell soll aus wenigen Finiten Elementen bestehen, überlegen Sie, welche Modelle sinnvoll sind. Die neutralen Fasern der Balken seien in Längsrichtung undehnbar – die Querschnitts-Schwerpunkte verschieben sich also nicht in Balken-Längsrichtung.
Gegeben: a, E I, F
Lösung mit Maxima
Header
Für das FE-Modell wollen wir nicht alle Sektionen der Feder modellieren - wir schneiden die Feder entlang ihrer Längsachse durch und nehmen eins der so entstandenen Elemente exemplarisch heraus.

Von diesen Elementen haben wir fünf in der Feder - die Längung dieses Elements der Feder entspricht also 1/5 der Feder-Längung in B.
Im Schnitt der horizontalen Sektionen mit der Längsachse der Feder ist das Schnittmoment jeweils Null - wir dürfen uns also an den Rändern unseres Sub-Systems ein Gelenk "denken" und mit dem hier gezeichneten System arbeiten.
Aber Achtung: so wie gezeichnet ist es statisch unbestimmt: wir können im Gleichgewicht beliebige Verschiebungen des Systems in Feder-Längsrichtung angeben.
| ✔ Geht's noch einfacher?: |
* Wie müsste ein System aussehen, das noch einfacher gestrickt ist?
|
/*******************************************************/
/* MAXIMA script */
/* version: wxMaxima 16.04.2 */
/* author: Andreas Baumgart */
/* last updated: 2020-01-10 */
/* ref: TM-C */
/* description: FEM-solution for spring section */
/*******************************************************/
Declarations
Wir haben also ein Ersatz-System mit drei Finiten Elementen und vier Knoten:
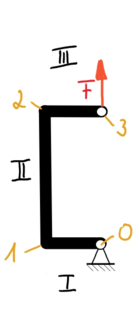
Die Knoten 0 und 3 entstehen in unserem Ersatz-System, weil hier das Biegemoment in den horizontalen Sektionen (I und III) Null ist. Diese beiden Sektionen sind nur a/2 lang, die vertikale Sektion ist a lang.
Damit das System in Längsrichtung festgelegt ist, führen wir in Knoten "0" ein gelenkiges Festlager ein - die Verschiebung in Knoten "3" ist dann die Auslenkung von Knoten "3" relativ zu Knoten "0".
Dementsprechnd haben die drei Finiten Elementen die Längen
- .
Die Element-Steifigkeitsmatrix kopieren wir aus Abschnitt FEM-Formulierung für den Euler-Bernoulli-Balken zu:
- .
/*******************************************************/
/* coordinates and boundary conditions */
l : [a/2,a,a/2];
norm : ŵ = F*a^3/(3*EI) * 5;
X : append(makelist(Q[i]= [W[i-1], Φ[i-1], W[i], Φ[i]],i,1,3),[Q[0]= [U[1], Ψ[1], Ψ[2], U[3]]]);
δX : subst([Q=δQ,W=δW,Φ=δΦ],X);
/* boundary conditions */
kinematics: [[W[0]= 0 , δW[0]= 0 ],
[W[1]= 0 , W[2]=0,δW[1]= 0 ,δW[2]=0],
[W[2]=-W[1], δW[2]=-δW[1] ]];
Coordinates
Für jedes Finite Element führen wir zuerst das standardisierte lokale x/z-Koordinatensystem![]() ein. Und wir definieren neue, anschauliche - globale - Koordinaten des Systems, um sie von den Standard-Koordinaten Wi , Φi unterscheiden zu können:
ein. Und wir definieren neue, anschauliche - globale - Koordinaten des Systems, um sie von den Standard-Koordinaten Wi , Φi unterscheiden zu können:
| Lokale Orts-Koordinaten xi, zi | Globale Knoten-Koordinaten Ui, Ψi |
|---|---|
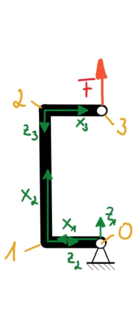 |
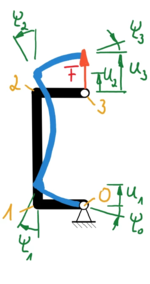 |
Wir haben also je Element die eingezeichneten globalen Knoten-Koordinaten
sowie die lokalen FE-Koordinaten
- .
die wir miteinander "verheiraten" müssen. Das machen wir beim Komponieren des Gesamt-Gleichungssystems.
Die virtuelle Formänderungsenergie eines Finiten Elements ist nun
- ,
mit
- .
Die virtuelle Arbeit der Kraft ist dabei
Aus den Bildern für die Knoten-Koordinaten oben lesen wir nun die (geometrischen) Rand- und Übergangsbedingungen ab und skizzieren darunter die Einarbeitung dieser Bedingungen in die virtuellen Formänderungsenergien.
| Element I | Element II | Element III |
|---|---|---|
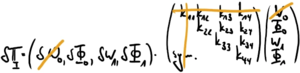 |
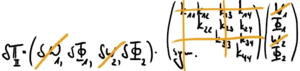 |
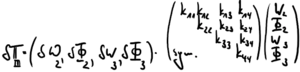 |
Dabei sind folgende Koordinaten sind in den drei Elementen gleich oder unterscheiden sich nur durch ein Vorzeichen:
Was noch fehlt ist die Übersetzung der lokalen in die globalen Koordinaten
| local | global | |
|---|---|---|
|
↔ |
/*******************************************************/
/* coordinates and boundary conditions */
l : [a/2,a,a/2];
norm : ŵ = F*a^3/(3*EI) * 5;
X : append(makelist(Q[i]= [W[i-1], Φ[i-1], W[i], Φ[i]],i,1,3),[Q[0]= [U[1], Ψ[1], Ψ[2], U[3]]]);
δX : subst([Q=δQ,W=δW,Φ=δΦ],X);
/* boundary conditions */
kinematics: [[W[0]= 0 , δW[0]= 0 ],
[W[1]= 0 , W[2]=0,δW[1]= 0 ,δW[2]=0],
[W[2]=-W[1], δW[2]=-δW[1] ]];
Assembly of System Matrices
Wir bauen nun das Gleichungssystem
zusammen, indem wir die Anteile der Element-Steifigkeitsmatrizen und die äußeren Lasten in die jeweiligen System Matrizen hineinaddieren.
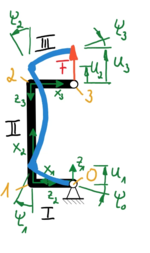
Dafür müssen wir die Koordinaten zwischen lokalen und globalen Koordinaten transformieren, nämlich
- .
Die virtuelle Formänderungsenergie ist dann
- für Sektion I:
- für Sektion II:
- für Sektion III:
Die Gesamt-Steifigkeitsmatrix aus Sektion 1 (rot) , Sektion 2 (grün) und Sektion 3 (blau) ist damit
- .
Die Spaltenmatrix der eingeprägten, äußeren Lasten auf das System ist dementsprechend
- .
/* system stiffness matrix K and system load matrix P */
/* assembly of system matrices */
A : [K[1]=Ki(a/2),K[2]=Ki( a ),K[3]=Ki(a/2), K[0] = zeromatrix(6,6)];
P : expand(makelist(δΠ[i] = subst(kinematics[i],transpose(subst(δX,δQ[i])).subst(A,K[i]).subst(X,Q[i])),i,1,3));
R : δW^a = F*δU[3];
/* translate to global coordinates */
globals: [ Φ[0] = Ψ[0], δΦ[0] = δΨ[0],
W[1] = U[1], δW[1] = δU[1],
Φ[1] = Ψ[1], δΦ[1] = δΨ[1],
Φ[2] =-Ψ[2], δΦ[2] =-δΨ[2],
W[3] =-U[3], δW[3] =-δU[3],
Φ[3] =-Ψ[3], δΦ[3] =-δΨ[3]];
P : sum(subst(globals,P[i]),i,1,3);
Y : [ Ψ[0], U[1], Ψ[1], Ψ[2], U[3], Ψ[3]];
δY : [δΨ[0], δU[1],δΨ[1],δΨ[2],δU[3],δΨ[3]];
eom : makelist(coeff(rhs(P)-rhs(R),δY[i])=0,i,1,6);
Solving
Das lineare Gleichungssystem lautet also
Und dessen Lösung ist
- .
/* solve ..... */
sol: solve(eom,Y)[1];
ACM : augcoefmatrix(eom, Y);
ole : [K[0] = submatrix(ACM,7), p = -col(ACM,7)];
print(subst(ole, K[0]),"*",transpose(Y),"=",subst(ole,p))$
Post-Processing
Wir normieren die Auslenkung des Systems mit
und plotten das System damit im ausgelenkten Zustand:
Die Auslenkung in Knoten 3 ist gleichzeitig die Längung der insgesamt 5 Sub-Systeme, die Auslenkung des Gesamtsystems in B ist demnach
und die gesuchte Ersatzfedersteifigkeit des Systems ist
- .
/* post-processing */
displ: makelist(expand(subst(norm,(subst(sol,subst(globals,subst(kinematics[j],subst(X,Q[j])))).transpose(subst([ℓ[i]=l[j]],phi))/ŵ))),j,1,3);
offset: subst(norm,subst(sol,U[1]/ŵ));
plot2d([[parametric, (1-t)/2, +subst([xi=t],displ[1]), [t,0,1]],
[parametric, +subst([xi=t],displ[2]), offset+t, [t,0,1]],
[parametric, ( t)/2, 1-subst([xi=t],displ[3]), [t,0,1]]],
[x,-1/2,2/2],[y,-0.1,1.4], [same_xy , true],
[legend,"I","II","III"])$
Links
- ...
Literature
- ...