Gelöste Aufgaben/FEB2: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
KKeine Bearbeitungszusammenfassung |
||
| (9 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 10: | Zeile 10: | ||
==Aufgabenstellung== | ==Aufgabenstellung== | ||
Die zwei Euler-Bernoulli-Balken ''AB'' (Länge ''a'') und ''BC'' (Länge ''2a'') sind in ''B'' fest verschweißt. Ihre Biegesteifigkeit ist ''EI''. Die Konstruktion ist in ''A'' fest eingespannt und in ''C'' durch ein verschiebliches Gelenklager gelagert. In ''B'' ist sie durch die Kraft ''F'' und das Moment ''M'' belastet. | |||
<onlyinclude> | <onlyinclude> | ||
[[Datei:FEB2-01.png|mini| | [[Datei:FEB2-01.png|mini|left|217x217px|Lageplan|alternativtext=]] | ||
Gesucht ist | Gesucht ist die Verschiebungen und Verdrehungen der Balken mit der [[Randwertprobleme/Methoden zur Lösung von Randwertproblemen/Finite Elemente Methode|Methode der Finiten ELemente]]. | ||
</onlyinclude> | </onlyinclude> | ||
Gegeben: ''a, E I, F, M'' | |||
== Lösung mit Maxima == | == Lösung mit Maxima == | ||
Berechnet werden sollten daf[r die Auslenkungen und Verdrehung der Punkte ''A, B'' und ''C''. Das Modell soll aus zwei Finiten Elementen bestehen, jeweils eins für den Abschnitt ''AB'' und ''BC''. Die neutralen Fasern der beiden Balken seien in Längsrichtung undehnbar – die Querschnitts-Schwerpunkte verschieben sich also nicht in Balken-Längsrichtung. | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Header | |||
|text= | |||
Hier müssen die Element-Steifigkeitsmatrizen für zwei Sektionen von [[Sources/Lexikon/Euler-Bernoulli-Balken|Euler-Bernoulli-Balken]] zusammengefügt (assembliert) werden. Die Schwierigkeit liegt darin, die Koordinaten in Punkt ''B'' passend zu wählen. | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
/*******************************************************/ | |||
/* MAXIMA script */ | |||
/* version: wxMaxima 16.04.2 */ | |||
/* author: Andreas Baumgart */ | |||
/* last updated: 2018-02-13 */ | |||
/* ref: TM-C */ | |||
/* description: FEM-solution for two rgidly connected */ | |||
/* sections */ | |||
/*******************************************************/ | |||
/*******************************************************/ | |||
/* MAXIMA script */ | |||
/* version: wxMaxima 16.04.2 */ | |||
/* author: Andreas Baumgart */ | |||
/* last updated: 2018-02-13 */ | |||
/* ref: TM-C */ | |||
/* description: FEM-solution for two rigidly connected */ | |||
/* sections */ | |||
/*******************************************************/ | |||
</syntaxhighlight> | |||
}} | |||
<!-------------------------------------------------------------------------------->{{MyCodeBlock|title=Declarations | |||
|text= | |||
Die Element-Steifigkeitsmatrix kopieren wir aus Abschnitt FEM-Formulierung für den Euler-Bernoulli-Balken zu: | |||
::<math>\displaystyle K_i(\ell_i) = \frac{E I}{\ell_i^3}\cdot \begin{pmatrix}12 & 6\cdot \ell_i & -12 & 6\cdot \ell_i\\ 6\cdot \ell_i & 4\cdot {{\ell_i}^{2}} & -6\cdot \ell_i & 2\cdot {{\ell_i}^{2}}\\ -12 & -6\cdot \ell_i & 12 & -6\cdot \ell_i\\ 6\cdot \ell_i & 2\cdot {{\ell_i}^{2}} & -6\cdot \ell_i & 4\cdot {{\ell_i}^{2}}\end{pmatrix}</math>. | |||
Die Element-Längen der zwei Finiten Elemente sind hier | |||
::<math>\begin{array}{l}\ell_1 = a\\ \ell_2 = 2\,a\end{array}</math>. | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
/***************************************************/ | |||
/* FEM-Formulierung+für+den+Euler-Bernoulli-Balken */ | |||
/*Trial-Fucntions*/ | |||
phi : [ (xi-1)^2*(2*xi+1), | |||
l[i]* xi *( xi-1)^2, | |||
- xi^2 *(2*xi-3), | |||
l[i]* xi^2 *( xi-1)]; | |||
Ki(l):= (EI/l^3)*matrix([ 12, 6*l ,-12 , 6*l ], | |||
[6*l, 4*l^2, -6*l, 2*l^2], | |||
[-12,-6*l , 12 ,-6*l ], | |||
[6*l, 2*l^2, -6*l, 4*l^2]); | |||
/***************************************************/ | |||
</syntaxhighlight> | |||
}} | |||
<!-------------------------------------------------------------------------------->{{MyCodeBlock|title=Coordinates | |||
|text= | |||
Zunächst hat das System mit zwei Finiten Elementen jeweils 4 Koordinaten, nämlich | |||
::<math>W_{i-1},\Phi_{i-1},W_{i},\Phi_{i}</math>. | |||
<table> | |||
<tr> | |||
<th style="background-color:#ff0000;">Sektion ''A-B''</th> | |||
<th style="background-color:#00ff00;">Sektion ''B-C''</th></tr> | |||
<tr><td style="width:50%; vertical-align:top">Die Sektion ist in A fest eingespannt, also ist hier | |||
::<math>W_{i-1} =0,\;\Phi_{i-1}=0.</math> | |||
Es bleiben die Verschiebung und Verdrehung in ''B'', also | |||
::<math>W_{i} = W_B,\; \Phi_{i} = \Phi_B</math>. | |||
</td> | |||
<td style="width:50%; vertical-align:top"> | |||
Die neutralen Fasern der Balken-Sektionen - also auch von ''AB'' - sind undehnbar. Die Punkte ''B'' und ''C'' können sich also nur in vertikale Richtung jeweils um ''W<sub>B</sub>'' verschieben. Durch diese Starrkörper-Verschiebung wird keine Arbeit geleistet - das tun nur die Lateral-Verschiebungen in ''w<sub>2</sub>(x<sub>2</sub>)''. | |||
Es ist also | |||
::<math>W_{i-1} =0,\;W_{i}=0.</math> | |||
Es bleiben also die Verdrehungen in ''B'' und ''C'' zu | |||
::<math>\Phi_{i-1} = \Phi_B,\; \Phi_{i} = \Phi_C</math> | |||
</td></tr> | |||
</table> | |||
[[Datei:FEB2-12.png|mini|Übertragung der Koordinaten.|alternativtext=|links]]Die verbleibenden Koordinaten des Gesamtsystems sind | |||
::<math>\underline{Q} = \left(\begin{array}{l}W_B\\\Phi_B\\\Phi_C\end{array}\right)</math> | |||
Das verformte System sieht dann so aus:[[Datei:FEB2-11.png|mini|245x245px|Verformte Lage.|alternativtext=]] | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
/* coordinates */ | |||
Q : [W[B], Phi[B],Phi[C]]; | |||
K[1] : submatrix(1,2,Ki( a),1,2); | |||
K[2] : submatrix(1,3,Ki(2*a),1,3); | |||
</syntaxhighlight> | |||
}} | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Assembly of System Matrices | |||
|text= | |||
Wir bauen das Gleichungssystem | |||
::<math>\underline{\underline{K}}\cdot\underline{Q} = \underline{P}</math> | |||
zusammen, indem wir die Anteile der Element-Steifigkeitsmatrizen und die äußeren Lasten in die jeweiligen System Matrizen hineinaddieren. | |||
Die virtuelle Formänderungsenergie ist | |||
<ul> | |||
<li>für Sektion ''AB'':<br/> | |||
<math>\delta\Pi_{AB} = \left(\delta W_B, \delta\Phi_B \right) \cdot \begin{pmatrix}\displaystyle\frac{12\cdot \mathit{EI}}{{{a}^{3}}} &\displaystyle -\frac{6\cdot \mathit{EI}}{{{a}^{2}}}\\ \displaystyle -\frac{6\cdot \mathit{EI}}{{{a}^{2}}} & \displaystyle\frac{4\cdot \mathit{EI}}{a}\end{pmatrix} \cdot \left(\begin{array}{l}W_B\\\Phi_B\end{array}\right)</math> und</li> | |||
<li>für Section ''BC'':<br/> | |||
<math>\delta\Pi_{BC} = \left(\delta\Phi_B, \delta\Phi_C \right) \cdot \begin{pmatrix}\displaystyle \frac{2\cdot \mathit{EI}}{a} & \displaystyle \frac{\mathit{EI}}{a}\\ \displaystyle \frac{\mathit{EI}}{a} & \displaystyle \frac{2\cdot \mathit{EI}}{a}\end{pmatrix} \cdot \left(\begin{array}{l}\Phi_B\\\Phi_C\end{array}\right)</math>.</li> | |||
</ul> | |||
Die Gesamt-Steifigkeitsmatrix aus <span style="color:#800000">Sektion AB (rot)</span> und <span style="color:#008000">Sektion 2 (grün)</span> ist damit | |||
::<math>\displaystyle \underline{\underline{K}} = \frac{E\,I}{a^3} \cdot | |||
\left(\begin{array}{ccc} | |||
{\color{red}{+12}}&{\color{red}{-6 a}}&0\\ | |||
{\color{red}{-6 a}}&{\color{red}{4 a^2}}+{\color{green}{2 a^2}}&{\color{green}{a^2}}\\ | |||
0&{\color{green}{a^2}}&{\color{green}{2 a^2}} | |||
\end{array} \right)</math>, | |||
Die Spaltenmatrix der eingeprägten, äußeren Lasten auf das System kommt aus | |||
::<math>\delta W^a = - F \cdot \delta W_B + M \cdot \delta \Phi_B </math> | |||
zu | |||
::<math>\displaystyle \underline{P} = \left(\begin{array}{r}-F\\M\\0\end{array}\right)</math>. | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
/* system stiffness matrix K and system load matrix P */ | |||
K[0] : zeromatrix(3,3); | |||
/* assembel */ | |||
for row:1 thru 2 do | |||
for col:1 thru 2 do | |||
(K[0][row ,col ] : K[0][row ,col ] + K[1][row,col], | |||
K[0][row+1,col+1] : K[0][row+1,col+1] + K[2][row,col]); | |||
P : matrix([-F],[M],[0]); | |||
</syntaxhighlight> | |||
}} | |||
<!--------------------------------------------------------------------------------> | <!--------------------------------------------------------------------------------> | ||
{{MyCodeBlock|title= | {{MyCodeBlock|title=Solving | ||
|text= | |text= | ||
Die Lösung des linearen Gleichungssystems liefert | |||
::<math>\begin{pmatrix}{{W}_{B}}\\ {{\Phi}_{B}}\\ {{\Phi}_{C}}\end{pmatrix}=\begin{pmatrix}\displaystyle \frac{12\cdot {{a}^{2}}\cdot M-11\cdot {{a}^{3}}\cdot F}{60\cdot \mathit{EI}}\\\displaystyle \frac{2\cdot a\cdot M-{{a}^{2}}\cdot F}{5\cdot \mathit{EI}}\\\displaystyle -\frac{2\cdot a\cdot M-{{a}^{2}}\cdot F}{10\cdot \mathit{EI}}\end{pmatrix}</math> | |||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
1 | /* solve by LU-factorisation */ | ||
sol: ratsimp(linsolve_by_lu(K[0],P)[1]); | |||
print(transpose(Q)=sol); | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Post/Processing | |||
|text= | |||
Solange | |||
::<math>\displaystyle M > \frac{11\cdot a\cdot F}{12}</math> | |||
sieht das System im ausgelenkten Zustand so aus:[[Datei:FEB2-21.png|mini|327x327px|Lage des verformten Systems.]] | |||
|code=NONE | |||
}} | }} | ||
| Zeile 34: | Zeile 198: | ||
'''Literature''' | '''Literature''' | ||
* ... | * ... | ||
Aktuelle Version vom 20. Dezember 2022, 11:03 Uhr
Aufgabenstellung
Die zwei Euler-Bernoulli-Balken AB (Länge a) und BC (Länge 2a) sind in B fest verschweißt. Ihre Biegesteifigkeit ist EI. Die Konstruktion ist in A fest eingespannt und in C durch ein verschiebliches Gelenklager gelagert. In B ist sie durch die Kraft F und das Moment M belastet.
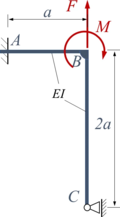
Gesucht ist die Verschiebungen und Verdrehungen der Balken mit der Methode der Finiten ELemente.
Gegeben: a, E I, F, M
Lösung mit Maxima
Berechnet werden sollten daf[r die Auslenkungen und Verdrehung der Punkte A, B und C. Das Modell soll aus zwei Finiten Elementen bestehen, jeweils eins für den Abschnitt AB und BC. Die neutralen Fasern der beiden Balken seien in Längsrichtung undehnbar – die Querschnitts-Schwerpunkte verschieben sich also nicht in Balken-Längsrichtung.
Header
Hier müssen die Element-Steifigkeitsmatrizen für zwei Sektionen von Euler-Bernoulli-Balken zusammengefügt (assembliert) werden. Die Schwierigkeit liegt darin, die Koordinaten in Punkt B passend zu wählen.
/*******************************************************/
/* MAXIMA script */
/* version: wxMaxima 16.04.2 */
/* author: Andreas Baumgart */
/* last updated: 2018-02-13 */
/* ref: TM-C */
/* description: FEM-solution for two rgidly connected */
/* sections */
/*******************************************************/
/*******************************************************/
/* MAXIMA script */
/* version: wxMaxima 16.04.2 */
/* author: Andreas Baumgart */
/* last updated: 2018-02-13 */
/* ref: TM-C */
/* description: FEM-solution for two rigidly connected */
/* sections */
/*******************************************************/
Declarations
Die Element-Steifigkeitsmatrix kopieren wir aus Abschnitt FEM-Formulierung für den Euler-Bernoulli-Balken zu:
- .
Die Element-Längen der zwei Finiten Elemente sind hier
- .
/***************************************************/
/* FEM-Formulierung+für+den+Euler-Bernoulli-Balken */
/*Trial-Fucntions*/
phi : [ (xi-1)^2*(2*xi+1),
l[i]* xi *( xi-1)^2,
- xi^2 *(2*xi-3),
l[i]* xi^2 *( xi-1)];
Ki(l):= (EI/l^3)*matrix([ 12, 6*l ,-12 , 6*l ],
[6*l, 4*l^2, -6*l, 2*l^2],
[-12,-6*l , 12 ,-6*l ],
[6*l, 2*l^2, -6*l, 4*l^2]);
/***************************************************/
Coordinates
Zunächst hat das System mit zwei Finiten Elementen jeweils 4 Koordinaten, nämlich
- .
| Sektion A-B | Sektion B-C |
|---|---|
| Die Sektion ist in A fest eingespannt, also ist hier
Es bleiben die Verschiebung und Verdrehung in B, also
|
Die neutralen Fasern der Balken-Sektionen - also auch von AB - sind undehnbar. Die Punkte B und C können sich also nur in vertikale Richtung jeweils um WB verschieben. Durch diese Starrkörper-Verschiebung wird keine Arbeit geleistet - das tun nur die Lateral-Verschiebungen in w2(x2). Es ist also Es bleiben also die Verdrehungen in B und C zu |
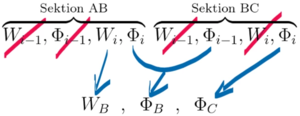
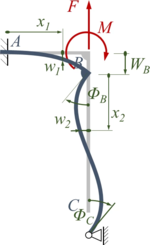
Die verbleibenden Koordinaten des Gesamtsystems sind
Das verformte System sieht dann so aus:
/* coordinates */
Q : [W[B], Phi[B],Phi[C]];
K[1] : submatrix(1,2,Ki( a),1,2);
K[2] : submatrix(1,3,Ki(2*a),1,3);
Assembly of System Matrices
Wir bauen das Gleichungssystem
zusammen, indem wir die Anteile der Element-Steifigkeitsmatrizen und die äußeren Lasten in die jeweiligen System Matrizen hineinaddieren.
Die virtuelle Formänderungsenergie ist
- für Sektion AB:
und - für Section BC:
.
Die Gesamt-Steifigkeitsmatrix aus Sektion AB (rot) und Sektion 2 (grün) ist damit
- ,
Die Spaltenmatrix der eingeprägten, äußeren Lasten auf das System kommt aus
zu
- .
/* system stiffness matrix K and system load matrix P */
K[0] : zeromatrix(3,3);
/* assembel */
for row:1 thru 2 do
for col:1 thru 2 do
(K[0][row ,col ] : K[0][row ,col ] + K[1][row,col],
K[0][row+1,col+1] : K[0][row+1,col+1] + K[2][row,col]);
P : matrix([-F],[M],[0]);
Solving
Die Lösung des linearen Gleichungssystems liefert
/* solve by LU-factorisation */
sol: ratsimp(linsolve_by_lu(K[0],P)[1]);
print(transpose(Q)=sol);
Post/Processing
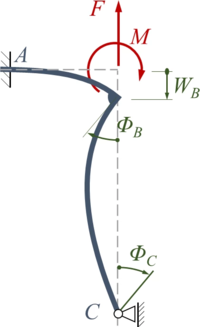
Solange
sieht das System im ausgelenkten Zustand so aus:
NONE
Links
- ...
Literature
- ...