Gelöste Aufgaben/FEB1: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
KKeine Bearbeitungszusammenfassung |
||
| (7 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 14: | Zeile 14: | ||
<onlyinclude> | <onlyinclude> | ||
[[Datei:FEB1-01.png|mini|Lageplan]] | [[Datei:FEB1-01.png|mini|left|Lageplan|200x200px]] | ||
Ein Hubschrauber-Rotor dreht mir der konstanten Winknelgeschwindigkeit Ω. | Ein Hubschrauber-Rotor dreht mir der konstanten Winknelgeschwindigkeit Ω. | ||
Das Rotor-Blatt ist aus Aluminium. Gesucht ist die FEM-Lösung für der Verschiebung der Querschnitte und die Dehnung der Querschnitte. | Das Rotor-Blatt ist aus Aluminium. Gesucht ist die FEM-Lösung für der Verschiebung der Querschnitte und die Dehnung der Querschnitte. | ||
| Zeile 20: | Zeile 20: | ||
== Lösung mit Maxima == | == Lösung mit Maxima == | ||
<!--------------------------------------------------------------------------------{{MyCodeBlock|title=Header | |||
|text= | |||
<!-------------------------------------------------------------------------------- | |||
Zu diesem Problem finden wir einfach eine analytische Lösung - die nutzen wir später, um unsere Ergebnisse dimensionslos zu machen. | Zu diesem Problem finden wir einfach eine analytische Lösung - die nutzen wir später, um unsere Ergebnisse dimensionslos zu machen. | ||
Ausgangspunkt ist die Gleichgewichtsbeziehung des [[Sources/Lexikon/Dehnstab|Dehnstabes]]. Die Streckenlast ''n'' (hier ''n(r)'') ist die Zentrifugalkraft - oder die [[Sources/Lexikon/D'Alembert'sche Trägheitskraft|D'Alembert'sche Trägheitskraft]] der Zentripetalbeschleunigung, also | Ausgangspunkt ist die Gleichgewichtsbeziehung des [[Sources/Lexikon/Dehnstab|Dehnstabes]]. Die Streckenlast ''n'' (hier ''n(r)'') ist die Zentrifugalkraft - oder die [[Sources/Lexikon/D'Alembert'sche Trägheitskraft|D'Alembert'sche Trägheitskraft]] der Zentripetalbeschleunigung, also | ||
<math>n(x) = -\varrho\,A\,r\,\Omega^2</math> . | ::<math>n(x) = -\varrho\,A\,r\,\Omega^2</math> . | ||
Die Bewegungsgleichung lautet dann | Die Bewegungsgleichung lautet dann | ||
<math>E\,A\,u''(r) = \varrho\,A\,r\,\Omega^2</math> . | ::<math>E\,A\,u''(r) = \varrho\,A\,r\,\Omega^2</math> . | ||
Die allgemeine Lösung ist | Die allgemeine Lösung ist | ||
<math>\displaystyle A\,E\,u(r)=-\frac{\varrho\,A\,{{\Omega}^{2}}\,{{r}^{3}}}{6}+{{c}_{1}}r+{{c}_{0}}</math> , | ::<math>\displaystyle A\,E\,u(r)=-\frac{\varrho\,A\,{{\Omega}^{2}}\,{{r}^{3}}}{6}+{{c}_{1}}r+{{c}_{0}}</math> , | ||
angepasst an die Randbedingungen | angepasst an die Randbedingungen | ||
<math>\begin{array}{l}u(0) = 0\\\displaystyle E\,A\,\frac{d}{dr}u|_{r=\ell_0} = 0\end{array}</math> | ::<math>\begin{array}{l}u(0) = 0\\\displaystyle E\,A\,\frac{d}{dr}u|_{r=\ell_0} = 0\end{array}</math> | ||
erhalten wir | erhalten wir | ||
<math>\displaystyle {u}(r)=\frac{3{{\ell}_{0}^{2}}\,r-r^3}{6\,A\,E}\cdot \varrho\,A\,{{\Omega}^{2}}</math> . | ::<math>\displaystyle {u}(r)=\frac{3{{\ell}_{0}^{2}}\,r-r^3}{6\,A\,E}\cdot \varrho\,A\,{{\Omega}^{2}}</math> . | ||
Als Bezugslänge gewinnen wir hier | Als Bezugslänge gewinnen wir hier | ||
<math>\begin{array}{ll}u_s &= u(\ell_0)\\&\displaystyle=\frac{{{\ell}_{0}^{3}}\,{{\Omega}^{2}}\varrho}{3E}\end{array}</math> | ::<math>\begin{array}{ll}u_s &= u(\ell_0)\\&\displaystyle=\frac{{{\ell}_{0}^{3}}\,{{\Omega}^{2}}\varrho}{3E}\end{array}</math> | ||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
1 | |||
/*******************************************************/ | |||
/* MAXIMA script */ | |||
/* version: wxMaxima 16.04.2 */ | |||
/* author: Andreas Baumgart */ | |||
/* last updated: 2018-02-01 */ | |||
/* ref: FENV */ | |||
/* description: FEM, */ | |||
/* computes static deflection and stresses */ | |||
/* in a rotating blade */ | |||
/*******************************************************/ | |||
/*******************************************************/ | |||
/* start: analytic solution */ | |||
eom : E*A*diff(u(r),r,2) = -rho*A*r*Omega^2; | |||
disp: subst([%c1=c[1],%c2=c[0]],integrate(integrate(eom,r),r)); | |||
disp: solve(disp,u(r))[1]; | |||
BC : [subst([r= 0 ],subst(disp,u(r))) = 0, | |||
subst([r=l[0]],diff(subst(disp,E*A*u(r)),r)) = 0]; | |||
sol[1]: solve(BC,[c[0],c[1]])[1]; | |||
disp : subst(sol[1],disp); | |||
params: [u[s] = subst([r=l[0]],subst(disp,u(r)))]; | |||
/* end: analytic solution */ | |||
/*******************************************************/ | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
<!------------------------------------------------------------------------------->{{MyCodeBlock|title=Declarations | |||
<! | |text= | ||
Für die Komposition der Bewegungsgleichungen brauchen wir die Element-Steifigkeitsmatrix und die Element-Lastmatrix. | |||
Wir gehen von gleichlangen Elementen aus, hier von | Wir gehen von gleichlangen Elementen aus, hier von | ||
<math>I =4</math> | ::<math>I =4</math> | ||
Elementen, also | Elementen, also | ||
<math>\displaystyle \ell_i = \frac{\ell_0}{I}</math>. | ::<math>\displaystyle \ell_i = \frac{\ell_0}{I}</math>. | ||
Wie im Abschnitt "[[Randwertprobleme/Methoden zur Lösung von Randwertproblemen/Finite Elemente Methode|Finite Elemente Methode]]" verwenden wir die linearen Ansatzfunktionen | Wie im Abschnitt "[[Randwertprobleme/Methoden zur Lösung von Randwertproblemen/Finite Elemente Methode|Finite Elemente Methode]]" verwenden wir die linearen Ansatzfunktionen | ||
<math>\phi_1 = 1-\xi \; \text{ und }\;\phi_1 = \xi</math>, | ::<math>\phi_1 = 1-\xi \; \text{ und }\;\phi_1 = \xi</math>, | ||
also | also | ||
<math>u_i(\xi_i) = U_{i-1} \cdot \phi_1(\xi_1) + U_{i} \cdot \phi_2(\xi_i)</math>. | ::<math>u_i(\xi_i) = U_{i-1} \cdot \phi_1(\xi_1) + U_{i} \cdot \phi_2(\xi_i)</math>. | ||
Die Element-Steifigkeitsmatrix ergibt sich für den Dehnstab zu | Die Element-Steifigkeitsmatrix ergibt sich für den Dehnstab zu | ||
<math>\displaystyle \underline{\underline{K}}_i = \frac{E\,A}{\ell_i}\cdot\left( \begin{array}{rr}1&-1\\-1&1\end{array}\right)</math>. | ::<math>\displaystyle \underline{\underline{K}}_i = \frac{E\,A}{\ell_i}\cdot\left( \begin{array}{rr}1&-1\\-1&1\end{array}\right)</math>. | ||
Die Element-Lastmatrix ist etwas schwieriger. Für ein einzelnes Element ''i'' ist | Die Element-Lastmatrix ist etwas schwieriger. Für ein einzelnes Element ''i'' ist | ||
<math>\displaystyle \delta W^a = \int_{\displaystyle r_i-1}^{\displaystyle r_{i}} \varrho\,A\,r\,\Omega^2 \cdot \delta u(r)\;dr</math>. | ::<math>\displaystyle \delta W^a = \int_{\displaystyle r_i-1}^{\displaystyle r_{i}} \varrho\,A\,r\,\Omega^2 \cdot \delta u(r)\;dr</math>. | ||
Mit | Mit | ||
<math>r = r_{i-1} + \ell_i\,\xi_i \text { und } r_{i-1} = (i-1)\cdot\ell_i</math> | ::<math>r = r_{i-1} + \ell_i\,\xi_i \text { und } r_{i-1} = (i-1)\cdot\ell_i</math> | ||
schreiben die Beziehung um zu | schreiben die Beziehung um zu | ||
<math>\displaystyle \delta W^a = \varrho\,A\,\Omega^2\,\ell_i^2 \cdot \int_{0}^{1} (i+\xi) \cdot \delta u(\xi)\;d\xi</math>, | ::<math>\displaystyle \delta W^a = \varrho\,A\,\Omega^2\,\ell_i^2 \cdot \int_{0}^{1} (i+\xi) \cdot \delta u(\xi)\;d\xi</math>, | ||
wir erhalten | wir erhalten | ||
<math>\underline{P}_i = \varrho\,A\,\Omega^2\,\ell_i^2 \left(\begin{array}{c}\displaystyle \frac{3\,i+1}{6}\\\displaystyle \frac{3\,i+2}{6}\end{array}\right)</math>. | ::<math>\underline{P}_i = \varrho\,A\,\Omega^2\,\ell_i^2 \left(\begin{array}{c}\displaystyle \frac{3\,i+1}{6}\\\displaystyle \frac{3\,i+2}{6}\end{array}\right)</math>. | ||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
1+1 | |||
/*******************************************************/ | |||
/* start: FEM solution */ | |||
/* Trial-Fucntions */ | |||
phi : [(1-xi), xi]; | |||
/* declare System Matrices */ | |||
K[i] : funmake('matrix, E*A*l[i]* | |||
makelist( | |||
makelist( | |||
integrate(diff(phi[j],xi)/l[i] * | |||
diff(phi[k],xi)/l[i], xi,0,1), | |||
j,1,2),k,1,2)); | |||
P[i] : funmake('matrix, rho*A*Omega^2*l[i]^2* | |||
makelist( | |||
integrate([(n+xi)*phi[j]], xi,0,1), | |||
j,1,2)); | |||
/* number of elements */ | |||
I : 4; | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
<math>\underline{\underline{K}} = \begin{pmatrix}\frac{AE}{{{\ell}_{i}}} & -\frac{AE}{{{\ell}_{i}}} & 0 & 0 & 0\\ -\frac{AE}{{{\ell}_{i}}} & \frac{2AE}{{{\ell}_{i}}} & -\frac{AE}{{{\ell}_{i}}} & 0 & 0\\ 0 & -\frac{AE}{{{\ell}_{i}}} & \frac{2AE}{{{\ell}_{i}}} & -\frac{AE}{{{\ell}_{i}}} & 0\\ 0 & 0 & -\frac{AE}{{{\ell}_{i}}} & \frac{2AE}{{{\ell}_{i}}} & -\frac{AE}{{{\ell}_{i}}}\\ 0 & 0 & 0 & -\frac{AE}{{{\ell}_{i}}} & \frac{AE}{{{\ell}_{i}}}\end{pmatrix}</math> | <!-------------------------------------------------------------------------------->{{MyCodeBlock|title=Equlibrium Conditions | ||
|text= | |||
Die Gleichgewichtsbeziehungen des Gesamtsystems erhalten wir durch aus der Addition aller virtuellen Arbeiten des Systems, praktisch durch das Hinzuaddieren der Anteile je Element in die System-Matrizen für ''K'' und ''P:'' | |||
::<math>\underline{\underline{K}} = \begin{pmatrix}\frac{AE}{{{\ell}_{i}}} & -\frac{AE}{{{\ell}_{i}}} & 0 & 0 & 0\\ -\frac{AE}{{{\ell}_{i}}} & \frac{2AE}{{{\ell}_{i}}} & -\frac{AE}{{{\ell}_{i}}} & 0 & 0\\ 0 & -\frac{AE}{{{\ell}_{i}}} & \frac{2AE}{{{\ell}_{i}}} & -\frac{AE}{{{\ell}_{i}}} & 0\\ 0 & 0 & -\frac{AE}{{{\ell}_{i}}} & \frac{2AE}{{{\ell}_{i}}} & -\frac{AE}{{{\ell}_{i}}}\\ 0 & 0 & 0 & -\frac{AE}{{{\ell}_{i}}} & \frac{AE}{{{\ell}_{i}}}\end{pmatrix}</math> | |||
und | und | ||
<math>\underline{P} = \varrho\,A\,\ell_i^2\,\Omega^2 \cdot \begin{pmatrix}\frac{1}{6}\\ 1\\ 2\\ 3\\ \frac{11}{6}\end{pmatrix}</math> | ::<math>\underline{P} = \varrho\,A\,\ell_i^2\,\Omega^2 \cdot \begin{pmatrix}\frac{1}{6}\\ 1\\ 2\\ 3\\ \frac{11}{6}\end{pmatrix}</math> | ||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
1+1 | |||
/* initiate system matrices */ | |||
K[0] : zeromatrix(I+1,I+1); | |||
P[0] : zeromatrix(I+1, 1 ); | |||
/* compose system matrices */ | |||
for e : 1 thru I do | |||
for row : 1 thru 2 do | |||
(P[0][e-1+row][ 1 ] : P[0][e-1+row][ 1 ]+subst([n=e-1],P[i][row][ 1 ]), | |||
for col : 1 thru 2 do | |||
K[0][e-1+row][e-1+col] : K[0][e-1+row][e-1+col]+ K[i][row][col]); | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
<!-------------------------------------------------------------------------------->Die geometrische Randbedingung ''U<sub>0</sub> = 0'' arbeiten wir ein, indem wir die erste Zeile des Gleichungssystem streichen sowie die erste Spalte der Steifigketsmatrix. | <!-------------------------------------------------------------------------------->{{MyCodeBlock|title=Boundary Conditions | ||
|text= | |||
Die geometrische Randbedingung ''U<sub>0</sub> = 0'' arbeiten wir ein, indem wir die erste Zeile des Gleichungssystem streichen sowie die erste Spalte der Steifigketsmatrix. | |||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
1 | /* incorporate geometric boundary conditions */ | ||
K[0] : submatrix( 1, K[0], 1); | |||
P[0] : submatrix( 1, P[0] ); | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
<math>\underline{\underline{K}}\cdot \underline{U} = \underline{P}</math> | <!-------------------------------------------------------------------------------->{{MyCodeBlock|title=Solving | ||
|text= | |||
Die Lösung des linearen Gleichungssystems | |||
::<math>\underline{\underline{K}}\cdot \underline{U} = \underline{P}</math> | |||
ist | ist | ||
<math>\underline{U} = \begin{pmatrix}\frac{47{{l}_{0}^{3}}\,{{\Omega}^{2}}\rho}{384E}\\ \frac{11{{l}_{0}^{3}}\,{{\Omega}^{2}}\rho}{48E}\\ \frac{39{{l}_{0}^{3}}\,{{\Omega}^{2}}\rho}{128E}\\ \frac{{{l}_{0}^{3}}\,{{\Omega}^{2}}\rho}{3E}\end{pmatrix}</math>. | ::<math>\underline{U} = \begin{pmatrix}\frac{47{{l}_{0}^{3}}\,{{\Omega}^{2}}\rho}{384E}\\ \frac{11{{l}_{0}^{3}}\,{{\Omega}^{2}}\rho}{48E}\\ \frac{39{{l}_{0}^{3}}\,{{\Omega}^{2}}\rho}{128E}\\ \frac{{{l}_{0}^{3}}\,{{\Omega}^{2}}\rho}{3E}\end{pmatrix}</math>. | ||
Oder - in dimensionsloser Form | Oder - in dimensionsloser Form | ||
<math>\displaystyle \frac{\underline{U}}{u_s} = \begin{pmatrix}\frac{47}{128}\\ \frac{11}{16}\\ \frac{117}{128}\\ 1\end{pmatrix}</math>. | ::<math>\displaystyle \frac{\underline{U}}{u_s} = \begin{pmatrix}\frac{47}{128}\\ \frac{11}{16}\\ \frac{117}{128}\\ 1\end{pmatrix}</math>. | ||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
1 | /* solve */ | ||
print(K[0],"*Q=",P[0])$ | |||
sol[2] : subst([l[i]=l[0]/I],linsolve_by_lu(K[0],P[0])[1]); | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
<!-------------------------------------------------------------------------------->{{MyCodeBlock|title=Post-Processing | |||
<!-------------------------------------------------------------------------------->[[Datei:FEB1-11.png|mini|Auslenkung ''u(x)''.]] | |text= | ||
[[Datei:FEB1-11.png|mini|Auslenkung ''u(x)''.]] | |||
Die Ergebnisse der FE-Rechnung und der analytischen Lösung können wir jetzt übereinander auftragen: | Die Ergebnisse der FE-Rechnung und der analytischen Lösung können wir jetzt übereinander auftragen: | ||
Die Dehnungen (und Spannungen) im Bauteil sind | Die Dehnungen (und Spannungen) im Bauteil sind | ||
<math>\displaystyle \varepsilon_{rr} = \frac{du}{dr}</math>. | ::<math>\displaystyle \varepsilon_{rr} = \frac{du}{dr}</math>. | ||
Auch dieses Ergebnis können wir auftragen:[[Datei:FEB1-12.png|mini|Dehnung ε(x).|alternativtext=|links]]<br clear="all"/> | |||
{{MyTip|title=Konstante Dehnung je Element|text=Was ausschaut wie ein Fehler - nämlich die "Treppenfunktion" für die Dehnung im FE-Modell - ist in Wirklichkeit die Folge unserer linearen Ansatzfunktionen. Diese abgeleitet liefern eine konstante Dehnung je Element.}} | {{MyTip|title=Konstante Dehnung je Element|text=Was ausschaut wie ein Fehler - nämlich die "Treppenfunktion" für die Dehnung im FE-Modell - ist in Wirklichkeit die Folge unserer linearen Ansatzfunktionen. Diese abgeleitet liefern eine konstante Dehnung je Element.}} | ||
| Zeile 159: | Zeile 213: | ||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
1+1 | |||
/* post-processing */ | |||
U : append([0],args(transpose(sol[2])[1]/subst(params,u[s]))); | |||
X : makelist(i,i,0,I)/I; | |||
plot2d([ratsimp(subst([r=xi*l[0]],subst(disp,u(r))/subst(params,u[s]))), | |||
[discrete, X, U],[discrete, X, U]], [xi,0,1], | |||
[legend, "analytic", "FEM", ""], | |||
[style, [lines,2,1], [lines,2,2], [points,2,2]], | |||
[point_type, asterisk], | |||
[xlabel, "ξ →"], [ylabel, "u →"])$ | |||
eps: subst(params,u[s])*makelist((U[i+1]-U[i]),i,1,I)/(l[0]/I); | |||
toPlot : append([expand(subst([r=xi*l[0]],diff(subst(disp,u(r)),r))/((l[0]^2*Omega^2*rho)/E))], | |||
makelist([discrete,[i-1,i]/I, [eps[i],eps[i]]/((l[0]^2*Omega^2*rho)/E)],i,1,I)); | |||
legends : append([legend, "analytic"],makelist(simplode(["Elem. ",i]),i,1,I)); | |||
plot2d(toPlot, [xi,0,1], legends, [y,0,0.6], | |||
[style, [lines,2]], | |||
[xlabel, "ξ →"], [ylabel, "ε/((l^2 ω^2 ρ/E) →"])$ | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
Aktuelle Version vom 9. März 2021, 11:20 Uhr
Aufgabenstellung
Auch wenn es nicht so aussieht: für das rotierende Rotorblatt suchen wir eine statische Lösung - das Problem heißt "quasistatisch".
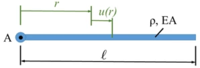
Ein Hubschrauber-Rotor dreht mir der konstanten Winknelgeschwindigkeit Ω. Das Rotor-Blatt ist aus Aluminium. Gesucht ist die FEM-Lösung für der Verschiebung der Querschnitte und die Dehnung der Querschnitte.
Lösung mit Maxima
Declarations
Für die Komposition der Bewegungsgleichungen brauchen wir die Element-Steifigkeitsmatrix und die Element-Lastmatrix.
Wir gehen von gleichlangen Elementen aus, hier von
Elementen, also
- .
Wie im Abschnitt "Finite Elemente Methode" verwenden wir die linearen Ansatzfunktionen
- ,
also
- .
Die Element-Steifigkeitsmatrix ergibt sich für den Dehnstab zu
- .
Die Element-Lastmatrix ist etwas schwieriger. Für ein einzelnes Element i ist
- .
Mit
schreiben die Beziehung um zu
- ,
wir erhalten
- .
/*******************************************************/
/* start: FEM solution */
/* Trial-Fucntions */
phi : [(1-xi), xi];
/* declare System Matrices */
K[i] : funmake('matrix, E*A*l[i]*
makelist(
makelist(
integrate(diff(phi[j],xi)/l[i] *
diff(phi[k],xi)/l[i], xi,0,1),
j,1,2),k,1,2));
P[i] : funmake('matrix, rho*A*Omega^2*l[i]^2*
makelist(
integrate([(n+xi)*phi[j]], xi,0,1),
j,1,2));
/* number of elements */
I : 4;
Equlibrium Conditions
Die Gleichgewichtsbeziehungen des Gesamtsystems erhalten wir durch aus der Addition aller virtuellen Arbeiten des Systems, praktisch durch das Hinzuaddieren der Anteile je Element in die System-Matrizen für K und P:
und
/* initiate system matrices */
K[0] : zeromatrix(I+1,I+1);
P[0] : zeromatrix(I+1, 1 );
/* compose system matrices */
for e : 1 thru I do
for row : 1 thru 2 do
(P[0][e-1+row][ 1 ] : P[0][e-1+row][ 1 ]+subst([n=e-1],P[i][row][ 1 ]),
for col : 1 thru 2 do
K[0][e-1+row][e-1+col] : K[0][e-1+row][e-1+col]+ K[i][row][col]);
Boundary Conditions
Die geometrische Randbedingung U0 = 0 arbeiten wir ein, indem wir die erste Zeile des Gleichungssystem streichen sowie die erste Spalte der Steifigketsmatrix.
/* incorporate geometric boundary conditions */
K[0] : submatrix( 1, K[0], 1);
P[0] : submatrix( 1, P[0] );
Solving
Die Lösung des linearen Gleichungssystems
ist
- .
Oder - in dimensionsloser Form
- .
/* solve */
print(K[0],"*Q=",P[0])$
sol[2] : subst([l[i]=l[0]/I],linsolve_by_lu(K[0],P[0])[1]);
Post-Processing
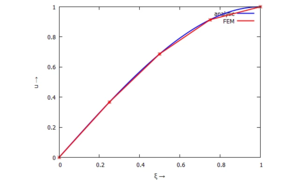
Die Ergebnisse der FE-Rechnung und der analytischen Lösung können wir jetzt übereinander auftragen:
Die Dehnungen (und Spannungen) im Bauteil sind
- .
Auch dieses Ergebnis können wir auftragen:
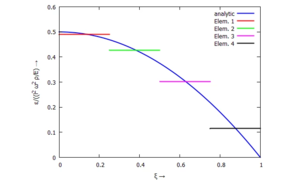
| ✔ Konstante Dehnung je Element: |
| Was ausschaut wie ein Fehler - nämlich die "Treppenfunktion" für die Dehnung im FE-Modell - ist in Wirklichkeit die Folge unserer linearen Ansatzfunktionen. Diese abgeleitet liefern eine konstante Dehnung je Element. |
/* post-processing */
U : append([0],args(transpose(sol[2])[1]/subst(params,u[s])));
X : makelist(i,i,0,I)/I;
plot2d([ratsimp(subst([r=xi*l[0]],subst(disp,u(r))/subst(params,u[s]))),
[discrete, X, U],[discrete, X, U]], [xi,0,1],
[legend, "analytic", "FEM", ""],
[style, [lines,2,1], [lines,2,2], [points,2,2]],
[point_type, asterisk],
[xlabel, "ξ →"], [ylabel, "u →"])$
eps: subst(params,u[s])*makelist((U[i+1]-U[i]),i,1,I)/(l[0]/I);
toPlot : append([expand(subst([r=xi*l[0]],diff(subst(disp,u(r)),r))/((l[0]^2*Omega^2*rho)/E))],
makelist([discrete,[i-1,i]/I, [eps[i],eps[i]]/((l[0]^2*Omega^2*rho)/E)],i,1,I));
legends : append([legend, "analytic"],makelist(simplode(["Elem. ",i]),i,1,I));
plot2d(toPlot, [xi,0,1], legends, [y,0,0.6],
[style, [lines,2]],
[xlabel, "ξ →"], [ylabel, "ε/((l^2 ω^2 ρ/E) →"])$
Links
- ...
Literature
- ...