Gelöste Aufgaben/FEAF: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
KKeine Bearbeitungszusammenfassung |
||
| (30 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 9: | Zeile 9: | ||
[[Category:Prinzip der virtuellen Verrückungen]] | [[Category:Prinzip der virtuellen Verrückungen]] | ||
== Aufgabenstellung == | |||
==Aufgabenstellung== | |||
Wir erkunden hier das Thema "Schwingungen von Kontinua" und bauen dabei auf die Ergebnisse zur Berechnung | Wir erkunden hier das Thema "Schwingungen von Kontinua" und bauen dabei auf die Ergebnisse zur Berechnung | ||
* der statischen Auslenkung mit FEM aus FEAD und | * der statischen Auslenkung mit [[Randwertprobleme/Methoden zur Lösung von Randwertproblemen/Finite Elemente Methode|FEM]] aus [[Gelöste Aufgaben/FEAD|FEAD]] und | ||
* der Schwingungen des Feder-Masse-Systems aus FEAE | * der Schwingungen des Feder-Masse-Systems aus [[Gelöste Aufgaben/FEAE|FEAE]] | ||
auf. | auf. | ||
<onlyinclude> | <onlyinclude> | ||
[[Datei:FEAB-01.png| | [[Datei:FEAB-01.png|left|mini|186x186px|Lageplan]] | ||
Gesucht ist die Längsschwingung des Stabes beim Loslassen aus seiner unverformten Referenzlage. Dabei arbeiten wir mit der [[Randwertprobleme/Methoden zur Lösung von Randwertproblemen/Finite Elemente Methode|Methode der Finiten Elemente]] zum Aufstellen der Bewegungsgleichungen. Die Integeationskonstanten der Lösung passen wir an die Anfangsbedingungen | Gesucht ist die Längsschwingung des Stabes beim Loslassen aus seiner unverformten Referenzlage. Dabei arbeiten wir mit der [[Randwertprobleme/Methoden zur Lösung von Randwertproblemen/Finite Elemente Methode|Methode der Finiten Elemente]] zum Aufstellen der Bewegungsgleichungen. Die Integeationskonstanten der Lösung passen wir an die Anfangsbedingungen | ||
* keine Anfangs-Auslenkung | * keine Anfangs-Auslenkung | ||
| Zeile 25: | Zeile 23: | ||
== Lösung mit Maxima == | == Lösung mit Maxima == | ||
<!-------------------------------------------------------------------------------->{{MyCodeBlock|title=Header | |||
|text= | |||
Für die mathematische Behandlung - insbesondere der Auflösung quadratischer Gleichungen - setzen wir in Maxima voraus, dass | |||
::<math>E > 0,\;\;\;A>0,\;\;\;\ell_0>0</math> . | |||
Später brauchen wir für die dimensionslose Formulierung noch eine Bezugszeit ''t<sub>Bez</sub>'' und eine Bezugslänge ''l<sub>Bez</sub>''. | |||
Dazu nehmen wir eine "Anleihe" bei der analytischen Lösung des Schwingungsproblems (vgl. Aufgabe [[Gelöste Aufgaben/SKER|SKER]]): | |||
<table class="wikitable"> | |||
<tr><th style="vertical-align:top;">Analytische Lösung: homohener Lösungsanteil </th> | |||
<th style="vertical-align:top;">Analytische Lösung: partikularer Lösungsanteil</th></tr> | |||
<tr><td style="vertical-align:top;> | |||
Die partielle Bewegungsgleichung des Stabes | |||
::<math>\varrho\,A\cdot\ddot{u}-E\,A\cdot{u}'' = 0</math> | |||
hat Lösungen | |||
::<math>\displaystyle u(x,t) = \sum_{i=1}^I U_i\cdot\sin(\kappa_i\cdot x)\cdot\cos(\omega_{0,i}\cdot t)</math>, | |||
die für | |||
::<math>\displaystyle \kappa_i=\frac{{\pi}\; \left(2\,i-1\right) }{2\;{{l}_{0}}}\; ; \; i\ge1</math> | |||
und | |||
::<math>\omega_0 = \pi \sqrt{\displaystyle \frac{E}{\varrho\;\ell_0^2}\left( i\cdot\left(i-1\right)+\frac{1}{4}\right) }</math> | |||
unsere Randbedingungen erfüllen. | |||
Für die langsamste Eigenmode ist | |||
::<math>\displaystyle \omega_{0,1} = \frac{\pi}{2\,\ell_0}\cdot\sqrt{\displaystyle \frac{E}{\varrho}}</math> , also ist | |||
<math>\begin{array}{ll}T_1 &= \displaystyle \frac{2\pi}{\omega_{0,1}}\\&=4\,\ell_0 \sqrt{\displaystyle \frac{\varrho}{E}}\end{array}</math> | |||
und wir wählen | |||
::<math>t_{Bez} := T</math> . | |||
</td> | |||
<!--------------------------------------------------> | |||
<td style="vertical-align:top;> | |||
Der partikulare Lösungsanteil ist | |||
::<math>\displaystyle u_p(x) = \varrho\;g\,\frac{\ell_0^2}{E}\;\xi \left(1 - \frac{\xi}{2}\right)\;\; ; \; \xi=\left(\frac{x}{\ell_0}\right)</math> . | |||
Die statische Auslenkung am unteren Ende ist demnach | |||
::<math>\begin{array}{ll}\displaystyle u_p(\ell_0) &\displaystyle = \varrho\,g\, \frac{\ell_0^2}{2\,E}\\&\displaystyle =: u_s\end{array}</math> . | |||
Wir wählen | |||
::<math>\ell_{Bez} := u_s</math> . | |||
</td></tr> | |||
</table> | |||
'''Modell-Parameter''' | |||
Für die Diskretisierung wählen wir als Anzahl der Finiten Elemente | |||
::<math>\displaystyle I = 2</math> | |||
und damit je Element | |||
::<math>\displaystyle \ell_i = \frac{\ell_0}{I}</math>. | |||
Wir wählen lineare Ansatzfunktionen je Element, also | |||
::<math>\phi_1 = 1-\xi \; ; \; \phi_2 = \xi.</math> | |||
Die abhängigen Koordinaten des [[Randwertprobleme/Methoden zur Lösung von Randwertproblemen/Finite Elemente Methode|FEM]]-Modells sind dann zunächst - bis zum Einarbeiten der Randbedingungen - | |||
::<math>\underline{Q}_t = \left(\begin{array}{c}U_0(t)\\U_1(t)\\\vdots \\U_I(t)\\ \end{array}\right)</math>. | |||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
1+1 | |||
/*******************************************************/ | |||
/* MAXIMA script */ | |||
/* version: wxMaxima 16.04.2 */ | |||
/* author: Andreas Baumgart */ | |||
/* last updated: 2018-01-07 */ | |||
/* ref: FEM, PVMPE using two coordinates */ | |||
/* description: solve by principle virt. Work */ | |||
/*******************************************************/ | |||
/* settings */ | |||
workdir: "C:\\Users\\X...X\\plots\\"; | |||
/* assumptions */ | |||
assume(E>0,A>0,l[0]>0); | |||
/* start: include these results */ | |||
/* from the analytical solution - see "solved problems": SKER */ | |||
sol[1] : [kappa=(2*%pi*i-%pi)/(2*l[0]),omega[0]^2=(4*%pi^2*E*i^2-4*%pi^2*E*i+%pi^2*E)/(4*l[0]^2*rho)]$ | |||
u[p] : [u(x)=-(g*rho*x^2-2*l[0]*g*rho*x)/(2*E), | |||
U[i]=-32/(8*%pi^3*i^3-12*%pi^3*i^2+6*%pi^3*i-%pi^3)]$ | |||
abbrev : [omega[0,0] =(2*%pi)/T, | |||
omega[0,0]^2=(%pi^2*E)/(4*l[0]^2*rho), | |||
omega[0,0]=(%pi*sqrt(E))/(2*l[0]*sqrt(rho)), | |||
T=(4*l[0]*sqrt(rho))/sqrt(E)]$ | |||
params : [t=T*tau,u[s]=(l[0]^2*g*rho)/(2*E)]$ | |||
/* end: include these results */ | |||
/* choose number of finite elements :*/ | |||
I : 2; | |||
params: append(params, [l[i] = l[0]/I]); | |||
/* coordinates */ | |||
Q[t]: makelist( U[i](t),i,1,I); | |||
/* tial function */ | |||
phi : [1-xi, xi]; | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
<!-------------------------------------------------------------------------------->{{MyCodeBlock|title=Equilibrium Conditions | <!-------------------------------------------------------------------------------->{{MyCodeBlock|title=Equilibrium Conditions | ||
|text= | |text= | ||
Die Gleichgewichtsbedingung mit dem [[Werkzeuge/Gleichgewichtsbedingungen/Arbeitsprinzipe der Analytischen Mechanik/Prinzip der virtuellen Verrückungen|Prinzip der virtuellen Verrückungen]] setzen sich additiv aus | |||
::<math>\displaystyle \delta W = \sum_{i=1}^I \left(\delta W^a_i - \delta \Pi_i \right) + \delta W^a_R</math>, | |||
zusammen - also den virtuellen Arbeiten je Element zuzüglich von virtuellen Arbeiten am Rand. In unserem Beispiel ist allerdings | |||
::<math>\delta W^a_R = 0</math> | |||
Je Element sind die virtuelle Formänderungsenergie (vgl. [[Randwertprobleme/Methoden zur Lösung von Randwertproblemen/Finite Elemente Methode|Finite Elemente Methode]]) | |||
::<math>\delta \Pi_i = \left(\delta U_{i-1}, \delta U_{i} \right) \cdot \underline{\underline{K}}_i\cdot \left(\begin{array}{l}U_{i-1}(t)\\U_{i}(t) \end{array}\right)</math> | |||
mit der Element-Steifigkeitsmatrix | |||
::<math>\displaystyle \underline{\underline{K}}_i = \frac{E\,A}{\ell_i} \cdot \left(\begin{array}{rr}1&-1\\-1&1\end{array}\right)</math>. | |||
Und je Element sind die virtuelle Arbeit der [[Sources/Lexikon/D'Alembert'sche Trägheitskraft|D'Alembert'schen Trägheitskraft]] | |||
::<math>\delta W^{a,A}_i = - \left(\delta U_{i-1}, \delta U_{i} \right) \cdot \underline{\underline{M}}_i\cdot \left(\begin{array}{l}\ddot{U}_{i-1}(t)\\\ddot{U}_{i}(t) \end{array}\right)</math> | |||
mit der Element-Massenmatrix | |||
::<math>\displaystyle \underline{\underline{M}}_i = \frac{\varrho\,A\, \ell_i}{6} \cdot \left(\begin{array}{rr}2&1\\1&2\end{array}\right)</math>. | |||
Analog folgt für die virtuelle Arbeit der Gewichtskraft | |||
::<math>\delta W^{a,g}_i = \left(\delta U_{i-1}, \delta U_{i} \right) \cdot \underline{G}_i</math> | |||
mit | |||
::<math>\displaystyle \underline{G}_i = \frac{\varrho\,A\, g\, \ell_i}{2} \cdot \left(\begin{array}{rr}1\\1\end{array}\right)</math>. | |||
Die System-Matrizen komponieren wir nun durch Hinzuaddieren der Anteile je Element. | |||
Beispiel: die Gesamt-Steifigkeitsmatrix für I=4: | |||
::<math>\displaystyle \underline{\underline{K}} = \frac{E\,A}{\ell_i} \cdot \left(\begin{array}{ccccc} | |||
+\color{red}1&-\color{red}1&0&0&0\\ | |||
-\color{red}1&\color{red}1\color{black}+\color{green}1&-\color{green}1&0&0\\ | |||
0&-\color{green}1&\color{green}1\color{black}+\color{blue}1&-\color{blue}1&0\\ | |||
0&0&-\color{blue}1&+\color{blue}1\color{black}+1&-1\\ | |||
0&0&0&-1&1 | |||
\end{array}\right)</math> | |||
Die Beiträge der vier Elemente sind hier in rot, grün, blau und schwarz eingefärbt. | |||
In Matrix-Schreibweise lautet die Bewegungsgleichung des Gesamt-Systems jetzt: | |||
::<math>\underline{\underline{M}}\cdot\underline{\ddot{Q}} + \underline{\underline{K}}\cdot\underline{Q} = \underline{G}</math>. | |||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
1+1 | /*elemente mass matrix */ | ||
M[i] : rho*A*l[i]*makelist( | |||
makelist(integrate( | |||
phi[j]*phi[k], xi,0,1) ,j,1,2), | |||
k,1,2); | |||
/*elemente stiffness matrix */ | |||
K[i] : E*A/l[i]*makelist( | |||
makelist(integrate( | |||
diff(phi[j],xi)*diff(phi[k],xi),xi,0,1) ,j,1,2), | |||
k,1,2); | |||
/*elemente load col-matrix */ | |||
G[i] : rho*A*l[i]*g*makelist(integrate(phi[j], xi,0,1) ,j,1,2);/* compose total system matrices */ | |||
M[0] : zeromatrix(I+1,I+1)$ | |||
K[0] : zeromatrix(I+1,I+1)$ | |||
G[0] : zeromatrix(I+1, 1)$ | |||
for e:1 thru I do | |||
for row:1 thru 2 do | |||
(for col:1 thru 2 do | |||
(K[0][(e-1)+row][(e-1)+col] : K[0][(e-1)+row][(e-1)+col] + K[i][row][col], | |||
M[0][(e-1)+row][(e-1)+col] : M[0][(e-1)+row][(e-1)+col] + M[i][row][col]), | |||
G[0][(e-1)+row][1] : G[0][(e-1)+row][1] + G[i][row])$ | |||
/* insert boundary conditions */ | |||
M[0] : submatrix(1,M[0],1); | |||
K[0] : submatrix(1,K[0],1); | |||
G[0] : submatrix(1,G[0] ); | |||
/* control print-out */ | |||
print(M[0],"∙",transpose(diff(Q[t],t,2)),"+",K[0],"∙",transpose(Q[t]),"=",G[0])$ | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
<!-------------------------------------------------------------------------------->{{MyCodeBlock|title=Solving | <!-------------------------------------------------------------------------------->{{MyCodeBlock|title=Solving | ||
|text= | |text= | ||
Die Lösung des Anfangswertproblems setzt sich aus zwei Teilen zusammen: | |||
* der partikularen Lösung, die die Rechte Seite "''G''" erfüllt und | |||
* der homogenen Lösung, die die Rechte Seite "''0''" erfüllt. | |||
Die Gesamtlösung ''Q<sub>t</sub>'' setzt sich nun - bei diesem linearen System - additiv aus partikularer ''Q<sub>p</sub>'' und ''Q<sub>h</sub>'' homogener Lösung zusammen: | |||
::<math>\underline{Q}_t(t) = \underline{Q}_p(t) + \underline{Q}_h(t)</math>. | |||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
/**************** total solution */ | |||
Q[t] : Q[p] + Q[h]; | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
<!-------------------------------------------------------------------------------->{{MyCodeBlock|title=Right-Hand-Side Approach | <!-------------------------------------------------------------------------------->{{MyCodeBlock|title=Right-Hand-Side Approach | ||
|text= | |text= | ||
Die rechte Seite der Bewegungsgleichung ''G'' ist nicht zeitabhängig - sie ist statisch. Also ist auch die Lösung ''Q<sub>p</sub>'' statisch, wir suchen nach der Lösung des Gleichungssystems | |||
::<math>\underline{\underline{K}}\cdot\underline{Q}_p = \underline{G}</math> | |||
und die ist | |||
::<math>\underline{Q}_p = \begin{pmatrix}\displaystyle \frac{3g\,{{l}_{i}^{2}}\rho}{2E}\\\displaystyle \frac{2g\,{{l}_{i}^{2}}\rho}{E}\end{pmatrix}</math> | |||
Mit u<sub>s</sub> also | |||
::<math>\underline{Q}_p = u_s\cdot \begin{pmatrix} \frac{3}{4}\\ 1\end{pmatrix}</math>. | |||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
1 | /***************************************************************************/ | ||
/* p a r t i c u l a r s o l u t i o n */ | |||
/***************************************************************************/ | |||
Q[p] : linsolve_by_lu(K[0],G[0])[1]; | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
<!-------------------------------------------------------------------------------->{{MyCodeBlock|title=Homogeneous Solution | <!-------------------------------------------------------------------------------->{{MyCodeBlock|title=Homogeneous Solution | ||
|text= | |text= | ||
Zur Lösung der homogenen Bewegungsgleichung | |||
::<math>\underline{\underline{M}}\cdot\underline{\ddot{Q}} + \underline{\underline{K}}\cdot\underline{Q} = \underline{0}</math> | |||
setzen wir an | |||
::<math>\displaystyle \underline{Q}_h = \underline{\hat{Q}}_h\cdot e^{\lambda\cdot t}</math> | |||
und erhalten das [[Werkzeuge/Lösungsbausteine der Mathematik/Eigenwertprobleme|Eigenwertproblem]] | |||
::<math>\underbrace{\left(\lambda^2 \underline{\underline{M}} + \underline{\underline{K}}\right)}_{=: \displaystyle \underline{\underline{D}}}\cdot\underline{\hat{Q}}_h = \underline{0}</math> | |||
mit | |||
<table> | |||
<tr><td>den Eigenwerten</td><td><math>\lambda</math> und</td></tr> | |||
<tr><td>den Eigenvektoren</td><td><math>\displaystyle \underline{\hat{Q}}_{h}</math>.</td></tr> | |||
</table> | |||
Die Berechnung der Eigenwerte ''λ'' wird einfacher mit | |||
::<math>\lambda^2 = -\Lambda</math> | |||
und wir transformieren parallel die Bewegungsgleichungen auf die dimensionslose Zeit | |||
::<math>\displaystyle \tau := \frac{t}{t_{Bez}}</math> mit <math>t_{Bez} = T.</math>, | |||
also | |||
::<math>\displaystyle \underline{\ddot{Q}} = \frac{d^2\underline{Q}}{d\tau^2}\cdot\underbrace{\frac{d^2\tau}{dt^2}}_{\displaystyle \frac{1}{T^2}}</math>. | |||
Wir finden zwei Eigenwerte aus der Bedingung <math>\det(\underline{\underline{D}})=0</math>: | |||
::<math>\begin{array}{lr}\Lambda_1 = &4.2\cdot10^1\\\Lambda_2 = &5.1\cdot 10^2\\\end{array}</math> | |||
und | |||
::<math>\begin{array}{lr}\lambda_1 = &j \cdot 6.4\\\lambda_2 = &j \cdot 23\\\end{array} \text{ mit } j := \sqrt{-1}</math>. | |||
Für die Matrix | |||
::<math>\displaystyle \underline{\underline{D}}(\lambda_i) = \lambda^2\cdot \frac{1}{T^2}\cdot \underline{\underline{M}} + \underline{\underline{K}}</math> | |||
stellen wir fest: | |||
Die Matrix hat | |||
* einen Rang (rank) von 1 - es gibt eine linear abhängige Zeile im Gleichungssystem und - entsprechend - | |||
* einen Rangabfall (nullity) von 1. | |||
Die Eigenvektoren spannen nun den Nullraum (nullspace) der Matrix auf. Normmert auf die Länge 1 sind das | |||
* für λ<sub>1</sub>: | |||
<math>\displaystyle \underline{\hat{Q}}_{h,1} = \left(\begin{array}{c}0.58\\0.82\end{array}\right)</math> und | |||
* für λ<sub>2</sub>: | |||
<math>\displaystyle \underline{\hat{Q}}_{h,2} = \left(\begin{array}{r}0.58\\-0.82 \end{array}\right)</math>. | |||
Die homogene Lösung der Bewegungsgleichung lautet damit | |||
::<math>\displaystyle \underline{{Q}}_{h}(t) = c_1\cdot \left(\begin{array}{r}0.58\\0.82\end{array}\right) \cdot e^{\displaystyle j\cdot 6.4 \cdot \tau} + c_2\cdot \left(\begin{array}{r}0.58\\-0.82 \end{array}\right) \cdot e^{\displaystyle j\cdot 23 \cdot \tau}</math> | |||
mit den Integrationskonstanten ''c<sub>1</sub>'' und ''c<sub>2</sub>''. Durch die komplexen Eigenwerte sind die beiden Integrationskonstanten nun auch komplexwertig, also | |||
::<math>\begin{array}{l}c_1 = c_{R,1} + j\cdot c_{I,1}\\c_2 = c_{R,2} + j\cdot c_{I,2}\end{array}</math>. | |||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
1+1 | /***************************************************************************/ | ||
/* h o m o g e n e o u s s o l u t i o n */ | |||
/***************************************************************************/ | |||
/* direct approach will usually not work for systems with now > 5 */ | |||
/* load(eigen); eigensystem: uniteigenvectors(subst(params, invert(M[0]).K[0])); */ | |||
/* -> not employed */ | |||
/**************** homogeneous solution */ | |||
/* solve eigenvalue problem */ | |||
D : -Lambda*(1/T)^2*M[0] + K[0]; | |||
D : subst(params, D); | |||
charPoly : determinant(D); | |||
/* eigenvalues */ | |||
eigval : solve(subst(abbrev,charPoly)=0,Lambda); | |||
eigval : subst(abbrev, eigval); | |||
/* save for later ....*/ | |||
eigvalList : makelist(subst(eigval[j],[%lambda[j]=%i*sqrt(Lambda)]),j,1,I); | |||
/* eigenvectors */ | |||
prop: [rnk = rank(ratsimp(expand(subst(eigval[1],subst(abbrev,D))))), | |||
nly = nullity(ratsimp(expand(subst(eigval[1],subst(abbrev,D)))))]; | |||
/* approach with "nullspace" works only for small problems .... */ | |||
if I<4 then | |||
(eigvec : makelist(apply (addcol, args (nullspace( | |||
ratsimp(expand(subst(abbrev,subst(eigval[i],D))))))),i,1,I)) | |||
else | |||
(eigvec : [], | |||
for i:1 thru I do | |||
(Ared : submatrix(I,ratsimp(expand(subst(abbrev,subst(eigval[i],D/(E*A/l[0])))))), | |||
bred : -float(col(Ared,I)), | |||
Ared : float(submatrix(Ared,I)), | |||
ev : addrow(linsolve_by_lu(Ared,bred)[1],[1]), | |||
eigvec : append(eigvec,[ev]))); | |||
/* norm eigenvectors (to be of length "1" */ | |||
eigvec : float(ratsimp(makelist(eigvec[i]/sqrt(eigvec[i].eigvec[i]),i,1,I))); | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
<!-------------------------------------------------------------------------------->{{MyCodeBlock|title=Adapt to Initial Conditions | <!-------------------------------------------------------------------------------->{{MyCodeBlock|title=Adapt to Initial Conditions | ||
|text= | |text= | ||
Diese vier reell-wertigen Integrationskonstanten bekommen wir aus vier Anfangsbedingungen für die beiden Massen, hier für ''I''=2 | |||
::<math>\begin{array}{l}U_1(0) = 0\\U_2(0) = 0\\ \dot{U}_1(0) = 0\\\dot{U}_2(0) = 0\end{array}</math>. | |||
Wir finden | |||
::<math>\displaystyle {{c}_{R,1}}=-2.5\;\frac{g\;\ell_i^2\;\varrho}{E},\;{{c}_{I,1}}=0,\;{{c}_{R,2}}=-0.074\;\frac{g\;\ell_i^2\;\varrho}{E},\;{{c}_{I,2}}=0</math>. | |||
und damit | |||
::<math>\underline{Q}_{h}(t) = \left(\begin{array}{r}-0.75\\-1.0\end{array}\right) + \left(\begin{array}{r}-0.73\\-1.0\end{array}\right)\cdot \cos(6.4\,\tau) + \left(\begin{array}{r}-0.021\\0.03\end{array}\right)\cdot \cos(23\,\tau)</math>. | |||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
1+1 | /***************************************************************************/ | ||
/* t o t a l ( c o m p o s e d ) s o l u t i o n */ | |||
/***************************************************************************/ | |||
/* adapt to initial values w[1](0)=0, w[2](0)=0 */ | |||
Q[h] : sum(subst(eigval[j],subst([%lambda[j]=%i*sqrt(Lambda),i=j], | |||
(c[Re,j]+%i*c[Im,j])*eigvec[j]*%e^(%lambda[j]*tau))),j,1,I); | |||
/* update Q[t]*/ | |||
Q[t] : ''(Q[t]); | |||
/* adapt to initial values */ | |||
intcons : flatten(makelist([c[Re,i],c[Im,i]], i, 1, I)); | |||
intcond : float(append(makelist(subst([tau=0], Q[t] )[i][1]=0,i,1,I), | |||
makelist(subst([tau=0],diff(Q[t],tau))[i][1]=0,i,1,I))); | |||
/* integration constants: */ | |||
sol[2] : ratsimp(solve(realpart(intcond),intcons)[1]); | |||
Q[t] : float(realpart(expand(subst(params,subst(sol[2],Q[t]/u[s])))))$ | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
<!-------------------------------------------------------------------------------->{{MyCodeBlock|title=Post-Processing | <!--------------------------------------------------------------------------------->{{MyCodeBlock|title=Post-Processing | ||
|text= | |text= | ||
[[Datei:FEAF-11.png|mini|''I=2'': Auslenkung ''u<sub>1</sub>(t), u<sub>2</sub>(t)''.]] | Die [[Randwertprobleme/Methoden zur Lösung von Randwertproblemen/Finite Elemente Methode|FEM]]-Lösung im Zeitbereich, angepasst an die Anfangsbedingungen, sieht nun so aus: | ||
[[Datei:FEAF-12.png|mini|''I=5'': Aulenkungen ''u<sub>i</sub>(t)''.]] | <table> | ||
<tr><td>[[Datei:FEAF-11.png|mini|''I=2'': Auslenkung ''u<sub>1</sub>(t), u<sub>2</sub>(t)''.]]</td> | |||
<td>[[Datei:FEAF-12.png|mini|''I=5'': Aulenkungen ''u<sub>i</sub>(t)''.]]</td></tr> | |||
</table> | |||
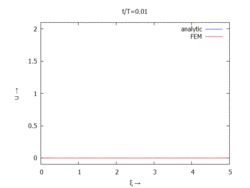
[[Datei:FEAF-21-animated.gif|''I=2'': Animation der Verschiebung des Endpuntkes.]] | Interessant ist die Auftragung von analytischer und FEM-Lösung als Animation über der Zeit: Man erkennt, wie die FE-Lösung sowohl Form als auch Zeitverlauf der analytischer Lösung erfasst, man erkennt jedoch auch, wie die FE-Lösung - Aufgrund ihrer höheren Eigenfrequenz - der analytischen Lösung vorauseilt. | ||
[[Datei:FEAF-22-animated.gif|''I=5'': Animation der Verschiebung des Endpunktes.]] | <table> | ||
<tr><td>[[Datei:FEAF-21-animated.gif|250px|''I=2'': Animation der Verschiebung des Endpuntkes.]]</td> | |||
<td>[[Datei:FEAF-22-animated.gif|250px|''I=5'': Animation der Verschiebung des Endpunktes.]]</td></tr> | |||
</table> | |||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
1+1 | |||
/* plot results */ | |||
legends: append([legend], makelist(simplode(["U[",i,"]"]),i,1,I)); | |||
plot2d(makelist(Q[t][i][1],i,1,I),[tau,0,4], legends, | |||
[xlabel, "τ/1 →"], [ylabel, "U/u[s] →"]); | |||
/* analytiv and FEM Solution */ | |||
analytic : append(sol[1], | |||
[omega[0]*t = sqrt(ratsimp(subst(abbrev,(subst(sol[1],omega[0]^2*T^2)))))*tau, | |||
x=l[0]*xi]); | |||
sol[3] : append([ratsimp(subst([x=xi*l[0]],subst(params,subst(u[p],u(x)/u[s]))))], | |||
makelist(subst([i=j],subst(u[p],subst(analytic,U[i]*sin(kappa*x)*cos(omega[0]*t)))),j,1,10)); | |||
timeFcts : makelist(subst(eigvalList[i],%e^(%lambda[i]*tau)),i,1,I); | |||
Q[l] : subst(params,append([Q[p]/u[s]], | |||
realpart(makelist(coeff(subst(sol[2],Q[h]),timeFcts[i])/u[s]*timeFcts[i],i,1,I)))); | |||
sol[4] : append( [[0,0]], makelist([i, Q[t][i][1]],i,1,I)); | |||
toPlot: [subst([xi=xi/I], sum(sol[3][i],i,1,length(sol[3]))), | |||
[discrete, sol[4]]]; | |||
NSteps : 19$ | |||
fpprintprec: 4$ | |||
for j:0 thru 10*NSteps-1 do | |||
(tstep : simplode([if j<10 then "00" elseif j<100 then "0" else "",j]), | |||
plot2d(subst([tau=j/NSteps],toPlot),[xi,0,I], [y,-0.1,2.1], | |||
[title, simplode(["t/T=",float(j/NSteps+0.01)])], [legend, "analytic", "FEM"], | |||
[style, [lines,1,1], [lines,1,2]], [xlabel, "ξ →"], [ylabel, "u →"], | |||
[png_file,simplode([workdir,"FEM-",I,"-step-",tstep,".png"])]))$ | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
Aktuelle Version vom 9. März 2021, 11:18 Uhr
Aufgabenstellung
Wir erkunden hier das Thema "Schwingungen von Kontinua" und bauen dabei auf die Ergebnisse zur Berechnung
auf.
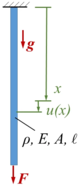
Gesucht ist die Längsschwingung des Stabes beim Loslassen aus seiner unverformten Referenzlage. Dabei arbeiten wir mit der Methode der Finiten Elemente zum Aufstellen der Bewegungsgleichungen. Die Integeationskonstanten der Lösung passen wir an die Anfangsbedingungen
- keine Anfangs-Auslenkung
- keine Anfangs-Geschwindigkeit
an.
Lösung mit Maxima
Header
Für die mathematische Behandlung - insbesondere der Auflösung quadratischer Gleichungen - setzen wir in Maxima voraus, dass
- .
Später brauchen wir für die dimensionslose Formulierung noch eine Bezugszeit tBez und eine Bezugslänge lBez.
Dazu nehmen wir eine "Anleihe" bei der analytischen Lösung des Schwingungsproblems (vgl. Aufgabe SKER):
| Analytische Lösung: homohener Lösungsanteil | Analytische Lösung: partikularer Lösungsanteil |
|---|---|
|
Die partielle Bewegungsgleichung des Stabes hat Lösungen
die für und unsere Randbedingungen erfüllen. Für die langsamste Eigenmode ist
und wir wählen
|
Der partikulare Lösungsanteil ist
Die statische Auslenkung am unteren Ende ist demnach
Wir wählen
|
Modell-Parameter
Für die Diskretisierung wählen wir als Anzahl der Finiten Elemente
und damit je Element
- .
Wir wählen lineare Ansatzfunktionen je Element, also
Die abhängigen Koordinaten des FEM-Modells sind dann zunächst - bis zum Einarbeiten der Randbedingungen -
- .
/*******************************************************/
/* MAXIMA script */
/* version: wxMaxima 16.04.2 */
/* author: Andreas Baumgart */
/* last updated: 2018-01-07 */
/* ref: FEM, PVMPE using two coordinates */
/* description: solve by principle virt. Work */
/*******************************************************/
/* settings */
workdir: "C:\\Users\\X...X\\plots\\";
/* assumptions */
assume(E>0,A>0,l[0]>0);
/* start: include these results */
/* from the analytical solution - see "solved problems": SKER */
sol[1] : [kappa=(2*%pi*i-%pi)/(2*l[0]),omega[0]^2=(4*%pi^2*E*i^2-4*%pi^2*E*i+%pi^2*E)/(4*l[0]^2*rho)]$
u[p] : [u(x)=-(g*rho*x^2-2*l[0]*g*rho*x)/(2*E),
U[i]=-32/(8*%pi^3*i^3-12*%pi^3*i^2+6*%pi^3*i-%pi^3)]$
abbrev : [omega[0,0] =(2*%pi)/T,
omega[0,0]^2=(%pi^2*E)/(4*l[0]^2*rho),
omega[0,0]=(%pi*sqrt(E))/(2*l[0]*sqrt(rho)),
T=(4*l[0]*sqrt(rho))/sqrt(E)]$
params : [t=T*tau,u[s]=(l[0]^2*g*rho)/(2*E)]$
/* end: include these results */
/* choose number of finite elements :*/
I : 2;
params: append(params, [l[i] = l[0]/I]);
/* coordinates */
Q[t]: makelist( U[i](t),i,1,I);
/* tial function */
phi : [1-xi, xi];
Equilibrium Conditions
Die Gleichgewichtsbedingung mit dem Prinzip der virtuellen Verrückungen setzen sich additiv aus
- ,
zusammen - also den virtuellen Arbeiten je Element zuzüglich von virtuellen Arbeiten am Rand. In unserem Beispiel ist allerdings
Je Element sind die virtuelle Formänderungsenergie (vgl. Finite Elemente Methode)
mit der Element-Steifigkeitsmatrix
- .
Und je Element sind die virtuelle Arbeit der D'Alembert'schen Trägheitskraft
mit der Element-Massenmatrix
- .
Analog folgt für die virtuelle Arbeit der Gewichtskraft
mit
- .
Die System-Matrizen komponieren wir nun durch Hinzuaddieren der Anteile je Element.
Beispiel: die Gesamt-Steifigkeitsmatrix für I=4:
Die Beiträge der vier Elemente sind hier in rot, grün, blau und schwarz eingefärbt.
In Matrix-Schreibweise lautet die Bewegungsgleichung des Gesamt-Systems jetzt:
- .
/*elemente mass matrix */
M[i] : rho*A*l[i]*makelist(
makelist(integrate(
phi[j]*phi[k], xi,0,1) ,j,1,2),
k,1,2);
/*elemente stiffness matrix */
K[i] : E*A/l[i]*makelist(
makelist(integrate(
diff(phi[j],xi)*diff(phi[k],xi),xi,0,1) ,j,1,2),
k,1,2);
/*elemente load col-matrix */
G[i] : rho*A*l[i]*g*makelist(integrate(phi[j], xi,0,1) ,j,1,2);/* compose total system matrices */
M[0] : zeromatrix(I+1,I+1)$
K[0] : zeromatrix(I+1,I+1)$
G[0] : zeromatrix(I+1, 1)$
for e:1 thru I do
for row:1 thru 2 do
(for col:1 thru 2 do
(K[0][(e-1)+row][(e-1)+col] : K[0][(e-1)+row][(e-1)+col] + K[i][row][col],
M[0][(e-1)+row][(e-1)+col] : M[0][(e-1)+row][(e-1)+col] + M[i][row][col]),
G[0][(e-1)+row][1] : G[0][(e-1)+row][1] + G[i][row])$
/* insert boundary conditions */
M[0] : submatrix(1,M[0],1);
K[0] : submatrix(1,K[0],1);
G[0] : submatrix(1,G[0] );
/* control print-out */
print(M[0],"∙",transpose(diff(Q[t],t,2)),"+",K[0],"∙",transpose(Q[t]),"=",G[0])$
Solving
Die Lösung des Anfangswertproblems setzt sich aus zwei Teilen zusammen:
- der partikularen Lösung, die die Rechte Seite "G" erfüllt und
- der homogenen Lösung, die die Rechte Seite "0" erfüllt.
Die Gesamtlösung Qt setzt sich nun - bei diesem linearen System - additiv aus partikularer Qp und Qh homogener Lösung zusammen:
- .
/**************** total solution */
Q[t] : Q[p] + Q[h];
Right-Hand-Side Approach
Die rechte Seite der Bewegungsgleichung G ist nicht zeitabhängig - sie ist statisch. Also ist auch die Lösung Qp statisch, wir suchen nach der Lösung des Gleichungssystems
und die ist
Mit us also
- .
/***************************************************************************/
/* p a r t i c u l a r s o l u t i o n */
/***************************************************************************/
Q[p] : linsolve_by_lu(K[0],G[0])[1];
Homogeneous Solution
Zur Lösung der homogenen Bewegungsgleichung
setzen wir an
und erhalten das Eigenwertproblem
mit
| den Eigenwerten | und |
| den Eigenvektoren | . |
Die Berechnung der Eigenwerte λ wird einfacher mit
und wir transformieren parallel die Bewegungsgleichungen auf die dimensionslose Zeit
- mit ,
also
- .
Wir finden zwei Eigenwerte aus der Bedingung :
und
- .
Für die Matrix
stellen wir fest:
Die Matrix hat
- einen Rang (rank) von 1 - es gibt eine linear abhängige Zeile im Gleichungssystem und - entsprechend -
- einen Rangabfall (nullity) von 1.
Die Eigenvektoren spannen nun den Nullraum (nullspace) der Matrix auf. Normmert auf die Länge 1 sind das
- für λ1:
und
- für λ2:
.
Die homogene Lösung der Bewegungsgleichung lautet damit
mit den Integrationskonstanten c1 und c2. Durch die komplexen Eigenwerte sind die beiden Integrationskonstanten nun auch komplexwertig, also
- .
/***************************************************************************/
/* h o m o g e n e o u s s o l u t i o n */
/***************************************************************************/
/* direct approach will usually not work for systems with now > 5 */
/* load(eigen); eigensystem: uniteigenvectors(subst(params, invert(M[0]).K[0])); */
/* -> not employed */
/**************** homogeneous solution */
/* solve eigenvalue problem */
D : -Lambda*(1/T)^2*M[0] + K[0];
D : subst(params, D);
charPoly : determinant(D);
/* eigenvalues */
eigval : solve(subst(abbrev,charPoly)=0,Lambda);
eigval : subst(abbrev, eigval);
/* save for later ....*/
eigvalList : makelist(subst(eigval[j],[%lambda[j]=%i*sqrt(Lambda)]),j,1,I);
/* eigenvectors */
prop: [rnk = rank(ratsimp(expand(subst(eigval[1],subst(abbrev,D))))),
nly = nullity(ratsimp(expand(subst(eigval[1],subst(abbrev,D)))))];
/* approach with "nullspace" works only for small problems .... */
if I<4 then
(eigvec : makelist(apply (addcol, args (nullspace(
ratsimp(expand(subst(abbrev,subst(eigval[i],D))))))),i,1,I))
else
(eigvec : [],
for i:1 thru I do
(Ared : submatrix(I,ratsimp(expand(subst(abbrev,subst(eigval[i],D/(E*A/l[0])))))),
bred : -float(col(Ared,I)),
Ared : float(submatrix(Ared,I)),
ev : addrow(linsolve_by_lu(Ared,bred)[1],[1]),
eigvec : append(eigvec,[ev])));
/* norm eigenvectors (to be of length "1" */
eigvec : float(ratsimp(makelist(eigvec[i]/sqrt(eigvec[i].eigvec[i]),i,1,I)));
Adapt to Initial Conditions
Diese vier reell-wertigen Integrationskonstanten bekommen wir aus vier Anfangsbedingungen für die beiden Massen, hier für I=2
- .
Wir finden
- .
und damit
- .
/***************************************************************************/
/* t o t a l ( c o m p o s e d ) s o l u t i o n */
/***************************************************************************/
/* adapt to initial values w[1](0)=0, w[2](0)=0 */
Q[h] : sum(subst(eigval[j],subst([%lambda[j]=%i*sqrt(Lambda),i=j],
(c[Re,j]+%i*c[Im,j])*eigvec[j]*%e^(%lambda[j]*tau))),j,1,I);
/* update Q[t]*/
Q[t] : ''(Q[t]);
/* adapt to initial values */
intcons : flatten(makelist([c[Re,i],c[Im,i]], i, 1, I));
intcond : float(append(makelist(subst([tau=0], Q[t] )[i][1]=0,i,1,I),
makelist(subst([tau=0],diff(Q[t],tau))[i][1]=0,i,1,I)));
/* integration constants: */
sol[2] : ratsimp(solve(realpart(intcond),intcons)[1]);
Q[t] : float(realpart(expand(subst(params,subst(sol[2],Q[t]/u[s])))))$
Post-Processing
Die FEM-Lösung im Zeitbereich, angepasst an die Anfangsbedingungen, sieht nun so aus:
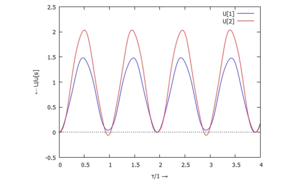 |
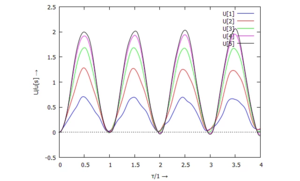 |
Interessant ist die Auftragung von analytischer und FEM-Lösung als Animation über der Zeit: Man erkennt, wie die FE-Lösung sowohl Form als auch Zeitverlauf der analytischer Lösung erfasst, man erkennt jedoch auch, wie die FE-Lösung - Aufgrund ihrer höheren Eigenfrequenz - der analytischen Lösung vorauseilt.
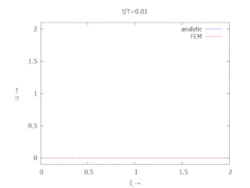 |
 |
/* plot results */
legends: append([legend], makelist(simplode(["U[",i,"]"]),i,1,I));
plot2d(makelist(Q[t][i][1],i,1,I),[tau,0,4], legends,
[xlabel, "τ/1 →"], [ylabel, "U/u[s] →"]);
/* analytiv and FEM Solution */
analytic : append(sol[1],
[omega[0]*t = sqrt(ratsimp(subst(abbrev,(subst(sol[1],omega[0]^2*T^2)))))*tau,
x=l[0]*xi]);
sol[3] : append([ratsimp(subst([x=xi*l[0]],subst(params,subst(u[p],u(x)/u[s]))))],
makelist(subst([i=j],subst(u[p],subst(analytic,U[i]*sin(kappa*x)*cos(omega[0]*t)))),j,1,10));
timeFcts : makelist(subst(eigvalList[i],%e^(%lambda[i]*tau)),i,1,I);
Q[l] : subst(params,append([Q[p]/u[s]],
realpart(makelist(coeff(subst(sol[2],Q[h]),timeFcts[i])/u[s]*timeFcts[i],i,1,I))));
sol[4] : append( [[0,0]], makelist([i, Q[t][i][1]],i,1,I));
toPlot: [subst([xi=xi/I], sum(sol[3][i],i,1,length(sol[3]))),
[discrete, sol[4]]];
NSteps : 19$
fpprintprec: 4$
for j:0 thru 10*NSteps-1 do
(tstep : simplode([if j<10 then "00" elseif j<100 then "0" else "",j]),
plot2d(subst([tau=j/NSteps],toPlot),[xi,0,I], [y,-0.1,2.1],
[title, simplode(["t/T=",float(j/NSteps+0.01)])], [legend, "analytic", "FEM"],
[style, [lines,1,1], [lines,1,2]], [xlabel, "ξ →"], [ylabel, "u →"],
[png_file,simplode([workdir,"FEM-",I,"-step-",tstep,".png"])]))$
Links
- ...
Literature
- ...