Werkzeuge/Lösungsbausteine der Mathematik/Gewöhnliche lineare Gleichungssysteme: Unterschied zwischen den Versionen
KKeine Bearbeitungszusammenfassung |
|||
| (10 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 88: | Zeile 88: | ||
Matrizen mit besondern Eigenschaften sind | Matrizen mit besondern Eigenschaften sind | ||
<ul> | |||
<math> \underline{\underline{1}} := \left(\begin{array}{cccc} 1& 0& \ldots & 0\\ 0& 1& \ldots & 0\\ \vdots &\vdots & \ddots & \vdots\\ 0& 0& \ldots & 1 \end{array}\right)</math>. Hier sind alle Diagonalelemente 1 und die restlichen Elemente 0. Oft wird E für diese Matrix verwendet, das kollidiert dann in der Mechanik mit der Matrix für den Zusammenhang zwischen Spannungen und Dehnungen eines isotropischen Materials (Hooks Gesetz / Spannungs-Dehnungs-Beziehung). | <li>die Einheitsmatrix:<br/> | ||
<math> \underline{\underline{1}} := \left(\begin{array}{cccc} 1& 0& \ldots & 0\\ 0& 1& \ldots & 0\\ \vdots &\vdots & \ddots & \vdots\\ 0& 0& \ldots & 1 \end{array}\right)</math>.<br/> | |||
Hier sind alle Diagonalelemente 1 und die restlichen Elemente 0. Oft wird E für diese Matrix verwendet, das kollidiert dann in der Mechanik mit der Matrix für den Zusammenhang zwischen Spannungen und Dehnungen eines isotropischen Materials ([[wikipedia:Hooke's_law|Hooks Gesetz]] / [[Sources/Lexikon/Spannungs-Dehnungs-Beziehung (Stress-Strain-Relation)|Spannungs-Dehnungs-Beziehung]]).</li> | |||
<li>die Nullmatrix ''0'':<br/> | |||
<math>\underline{\underline{ 0 }}</math><br/> | |||
alle Elemente der Matrix sind 0.</li> | |||
<li>Die Dreiecksmatrix:<br/>Hier sind alle Elemente ober- oder unterhalb der Haupt-Diagonalen 0.</li> | |||
<li>symmetrische Matrizen:<br/> Hier ist<br/><math>a_{i,j} = a_{j,i}</math>.</li> | |||
<li>Zeilenmatrix, Spaltenmatrix: Dies sind Matrizen, die nur eine Zeile oder nur eine Spalte besitzen.</li> | |||
</ul> | |||
{{Vorlage:MyWarning|title=Achtung|text=In der Mathematik und Mechanik werden hier unterschiedliche Begriffe verwendet. Die Mathematik bezeichnet eine Matrix mit nur einer Spalte oder Zeile als Vektor. Auch in Matlab heißt eine solche Matrix "Vektor". Für Ingenieure ist das keine gute Wahl: bei uns sind Vektoren gerichtete und orientierte Größen im Raum, keine Tabelle mit Objekten. | {{Vorlage:MyWarning|title=Achtung|text=In der Mathematik und Mechanik werden hier unterschiedliche Begriffe verwendet. Die Mathematik bezeichnet eine Matrix mit nur einer Spalte oder Zeile als Vektor. Auch in Matlab heißt eine solche Matrix "[[Sources/Lexikon/Vektor|Vektor]]". Für Ingenieure ist das keine gute Wahl: bei uns sind Vektoren gerichtete und orientierte Größen im Raum, keine Tabelle mit Objekten. | ||
Achtung}} | Achtung}} | ||
| Zeile 101: | Zeile 106: | ||
Ein Gleichungssystem heißt inhomogen, wenn die rechte Seite des Gleichungssystems ''b'' keine Null-Spaltenmatrix - kurz: nicht Null - ist. | Ein Gleichungssystem heißt inhomogen, wenn die rechte Seite des Gleichungssystems ''b'' keine Null-Spaltenmatrix - kurz: nicht Null - ist. | ||
Ein inhomogenes Gleichungssystem hat nur dann Lösungen, wenn die Spalten und Zeilen der Systemmatrix ''A'' linear unabhängig sind. Das prüft man mit über die Determinante | Ein inhomogenes Gleichungssystem hat nur dann Lösungen, wenn die Spalten und Zeilen der Systemmatrix ''A'' linear unabhängig sind. Das prüft man mit über die [[Sources/Lexikon/Determinante|Determinante]]. | ||
Lösungsbeispiele sind: | Lösungsbeispiele sind: | ||
{| class="wikitable" | {| class="wikitable" | ||
|+ | |+ | ||
!'''Matlab''' | !style="width:50%"|'''Matlab''' | ||
!'''Maxima''' | !'''Maxima''' | ||
|- | |- | ||
|[[Datei:GewöhnlicheLineareGleichungssysteme-Matlab.png| | |style="vertical-align:top"|[[Datei:GewöhnlicheLineareGleichungssysteme-Matlab.png|left|129px|<code>x = linsovle(A,b)</code>]] | ||
|[[Datei:GewöhnlicheLineareGleichungssysteme-linsolve by lu.png|mini|x : linsolve_by_lu(A,b);]] | |style="vertical-align:top"|[[Datei:GewöhnlicheLineareGleichungssysteme-linsolve by lu.png|left|mini|x : linsolve_by_lu(A,b);]] | ||
|- | |- | ||
| | |'''Code''':<br/> <code>x = linsolve(A,b)</code> | ||
|'''Code''':<br/> <code>x : linsolve_by_lu(A,b);</code> | |||
|} | |} | ||
| Zeile 135: | Zeile 132: | ||
= Inverse Matrix = | = Inverse Matrix = | ||
Die inverse einer Matrix ''A<sup>-1</sup>'' erfüllt | Die inverse einer Matrix ''A<sup>-1</sup>'' erfüllt | ||
::<math>\underline{\underline{A}}\cdot\underline{\underline{A}}^{-1} = \underline{\underline{1}}</math>. | |||
Für Anwendungen der Mechanik brauchen wir sie nicht. | Für Anwendungen der Mechanik brauchen wir sie nicht. | ||
| Zeile 140: | Zeile 139: | ||
Insbesondere ist | Insbesondere ist | ||
[[Datei:GewöhnlicheLineareGleichungssysteme-invM.png|left]] | ::[[Datei:GewöhnlicheLineareGleichungssysteme-invM.png|left]] | ||
<br clear="all"/> | |||
im numerischen Kontext verboten. Denn Matrizen zu invertieren ist | im numerischen Kontext verboten. Denn Matrizen zu invertieren ist | ||
Aktuelle Version vom 18. Februar 2021, 15:37 Uhr
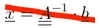
Ein lineares Gleichungssystem sind Gleichungen der Form
- .
Die gesuchten Größen xi treten nur linear in den Gleichungen auf, also nicht z.B. als xi2 oder √xi. Die Koeffizienten ai,j und die "rechte Seite" bi sind bekannte Größen.
In der Technischen Mechanik sind die unbekannten Größen üblicherweise
Matrix-Schreibweise
Für unsere Anwendungen brauchen wir genau so viele Gleichungen wie Unbekannte, also ist üblicherweise m=n. Struktur bringen wir in diese unübersichtliche Anordnung, indem wir sie als
formulieren: wir schreiben die Konstanten bi, die Unbekannten xi und deren Koeffizienten ai,j getrennt voneinander hin.
Diese rechteckige Anordnung unserer Größen nennen wir Matrizen (Singular: Matrix). Im Allgemeinen sind diese Matrizen einfach nur Tabellen, in die wir Objekte hineinschreiben. Einen physikalischen Sinn erhalten sie erst aus dem Kontext der linearen Gleichungen. Mit diesen Matrizen werden wir nach den Regeln der Linearen Algebra umgehen, sie miteinander addieren, subtrahieren und multiplizieren. Damit das in abstrakter Form übersichtlich wird, führen wir eine besondere Nomenklatur für die Abkürzungen von Matrizen ein: Mit
- ,
und
kürzen wir dann jedes lineare Gleichungssystem als
ab.
Bezeichnungen
Wir brauchen ein paar Begriffe für den Umgang mit Matrizen:
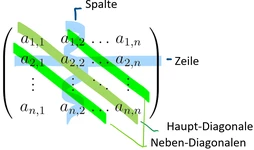
Wir kennzeichnen Matrizen:
Matrizen mit besondern Eigenschaften sind
- die Einheitsmatrix:
.
Hier sind alle Diagonalelemente 1 und die restlichen Elemente 0. Oft wird E für diese Matrix verwendet, das kollidiert dann in der Mechanik mit der Matrix für den Zusammenhang zwischen Spannungen und Dehnungen eines isotropischen Materials (Hooks Gesetz / Spannungs-Dehnungs-Beziehung). - die Nullmatrix 0:
alle Elemente der Matrix sind 0. - Die Dreiecksmatrix:
Hier sind alle Elemente ober- oder unterhalb der Haupt-Diagonalen 0. - symmetrische Matrizen:
Hier ist
. - Zeilenmatrix, Spaltenmatrix: Dies sind Matrizen, die nur eine Zeile oder nur eine Spalte besitzen.
| 🧨 Achtung: |
| In der Mathematik und Mechanik werden hier unterschiedliche Begriffe verwendet. Die Mathematik bezeichnet eine Matrix mit nur einer Spalte oder Zeile als Vektor. Auch in Matlab heißt eine solche Matrix "Vektor". Für Ingenieure ist das keine gute Wahl: bei uns sind Vektoren gerichtete und orientierte Größen im Raum, keine Tabelle mit Objekten. Achtung |
Lösung von inhomogenen Gleichungssystemen
Ein Gleichungssystem heißt inhomogen, wenn die rechte Seite des Gleichungssystems b keine Null-Spaltenmatrix - kurz: nicht Null - ist.
Ein inhomogenes Gleichungssystem hat nur dann Lösungen, wenn die Spalten und Zeilen der Systemmatrix A linear unabhängig sind. Das prüft man mit über die Determinante.
Lösungsbeispiele sind:
| Matlab | Maxima |
|---|---|
 x = linsovle(A,b) |
 |
Code:x = linsolve(A,b)
|
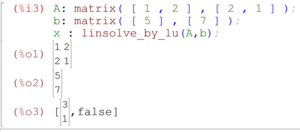
Code:x : linsolve_by_lu(A,b);
|
Lösung von homogenen Gleichungssystemen
Ein Gleichungssystem heißt homogen, wenn b = 0 also
Ein homogenes Gleichungssystem hat nur dann nichttriviale (= von Null verschiedene) Lösungen, wenn Spalten und Zeilen der Systemmatrix A linear abhängig sind. Das prüft man über die Determinante.
Damit ist die Lösung nicht eindeutig bestimmt - es gibt in den Lösungen immer mindestens eine Konstante, die frei gewählt werden kann.
Inverse Matrix
Die inverse einer Matrix A-1 erfüllt
- .
Für Anwendungen der Mechanik brauchen wir sie nicht.
Insbesondere ist
im numerischen Kontext verboten. Denn Matrizen zu invertieren ist
- teuer und
- ungenau.