Gelöste Aufgaben/StaF: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| (12 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 17: | Zeile 17: | ||
<onlyinclude> | <onlyinclude> | ||
[[Datei: | [[Datei:StaB-01.PNG|150px|left|mini|Stabwerk mit in den Knoten fest verbundenen Stäben.]] | ||
Gesucht ist ein Vergleich zwischen der klassischen Stabwerkstheorie und einer Herangehensweise, bei der wir eine feste Verbindung der Stäbe in den Knoten ansetzten. Grundlage des Modells ist die FEM-Lösung der Felddifferentialgleichung im Vergleich zur Lösung in Problemstellung | Gesucht ist ein Vergleich zwischen der klassischen Stabwerkstheorie und einer Herangehensweise, bei der wir eine feste Verbindung der Stäbe in den Knoten ansetzten. Grundlage des Modells ist die FEM-Lösung der Felddifferentialgleichung im Vergleich zur Lösung in Problemstellung „[[Gelöste_Aufgaben/StaB|StaB]]“. | ||
</onlyinclude> | </onlyinclude> | ||
Wir stellen das Modell des Stabwerks mit dem Prinzip der virtuellen Verrückungen auf und vergleichen, wie sich diese von der Herangehensweise aus | Wir stellen das Modell des Stabwerks mit dem Prinzip der virtuellen Verrückungen auf und vergleichen, wie sich diese von der Herangehensweise aus „Aufgabe [[Gelöste_Aufgaben/StaB|StaB]]“ mit der analytischen Lösung unterscheidet. | ||
== Lösung mit Maxima == | == Lösung mit Maxima == | ||
Wir nutzen das Computer-Algebra-System Maxima zur Lösung. Das macht hier Sinn, weil wir die Herangehensweise mit der aus Stab vergleichen wollen – für die wir ebenfalls Maxima eingesetzt haben. | Wir nutzen das Computer-Algebra-System Maxima zur Lösung. Das macht hier Sinn, weil wir die Herangehensweise mit der aus Stab vergleichen wollen – für die wir ebenfalls Maxima eingesetzt haben. | ||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Declarations | |||
|text= | |||
Wir übernehmen alle Vereinbarungen und Parameter aus der Problemformulierung „[https://numpedia.rzbt.haw-hamburg.de/index.php?title=Gel%C3%B6ste_Aufgaben/Stab Stab]“. | Wir übernehmen alle Vereinbarungen und Parameter aus der Problemformulierung „[https://numpedia.rzbt.haw-hamburg.de/index.php?title=Gel%C3%B6ste_Aufgaben/Stab Stab]“. | ||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
/*******************************************************/ | |||
/* MAXIMA script */ | |||
/* version: wxMaxima 21.05.2 */ | |||
/* author: Andreas Baumgart */ | |||
/* last updated: 2024-09-20 */ | |||
/* ref: NMM, Labor 2, dimensionsbehaftete */ | |||
/* Vorgehensweise */ | |||
/* description: finds the FEM solution for */ | |||
/* lab problem #2 */ | |||
/*******************************************************/ | |||
=== | assume(A>0,H>h,h>0, a>0); | ||
/*-----------------------------------------------------*/ | |||
/* Euler-Matrix */ | |||
DR(α) := matrix([ cos(α),sin(α), 0], | |||
[-sin(α),cos(α), 0], | |||
[ 0 , 0 , 1]); | |||
/* inverse of Euler-Matrix */ | |||
DI(α) := transpose(DR(α)); | |||
/* compose transforation matrix for rod (two ends ....)*/ | |||
DE(α) := matrix([ cos(α),-sin(α), 0, 0 , 0 , 0], | |||
[ sin(α), cos(α), 0, 0 , 0 , 0], | |||
[ 0 , 0 , 1, 0 , 0 , 0], | |||
[ 0 , 0 , 0, cos(α),-sin(α), 0], | |||
[ 0 , 0 , 0, sin(α), cos(α), 0], | |||
[ 0 , 0 , 0, 0 , 0 , 1]); | |||
/* for each rod, define | |||
* angle α, and | |||
* node-IDs | |||
at its start and end */ | |||
index : [[ 0 ,[1,3]], /* rod #1*/ | |||
[α[2],[2,3]], /* rod #2*/ | |||
[α[3],[3,4]], /* rod #3*/ | |||
[ 0 ,[2,4]] /* rod #4*/]; | |||
/* node - reference locations */ | |||
nodes: [[0,0],[0,sqrt(3)/2],[1/2,0],[0,sqrt(3)/2]]$ | |||
/*-----------------------------------------------------*/ | |||
/* system parameters */ | |||
params: [ℓ[1]=ℓ[0]/2, ℓ[2]=ℓ[0], ℓ[3]=ℓ[0], ℓ[4]=ℓ[0], | |||
α[2]=%pi/3,α[3]= -%pi/3, | |||
EA = E*A, EI = E*I, I=η*A^2/12]; | |||
moreParams: [A = a^2, ℓ[0]= 100*a]; | |||
</syntaxhighlight> | |||
}} | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Gleichgewichtsbedingungen | |||
|text= | |||
Für die Gleichgewichtsbedingung nach dem [https://numpedia.rzbt.haw-hamburg.de/index.php?title=Werkzeuge/Gleichgewichtsbedingungen/Arbeitsprinzipe_der_Analytischen_Mechanik/Prinzip_der_virtuellen_Verr%C3%BCckungen Prinzip der virtuellen Verrückungen] | Für die Gleichgewichtsbedingung nach dem [https://numpedia.rzbt.haw-hamburg.de/index.php?title=Werkzeuge/Gleichgewichtsbedingungen/Arbeitsprinzipe_der_Analytischen_Mechanik/Prinzip_der_virtuellen_Verr%C3%BCckungen Prinzip der virtuellen Verrückungen] | ||
::<math> | ::<math> | ||
| Zeile 38: | Zeile 92: | ||
benötigen wir die virtuelle Formänderungsenergie <math>\delta \Pi</math> und die virtuelle Arbeit der äußeren Kraft <math>\delta W^a</math> der äußeren Kräfte und Momente. | benötigen wir die virtuelle Formänderungsenergie <math>\delta \Pi</math> und die virtuelle Arbeit der äußeren Kraft <math>\delta W^a</math> der äußeren Kräfte und Momente. | ||
Mit den Konventionen für die Knoten-Verschiebungen aus [ | Mit den Konventionen für die Knoten-Verschiebungen aus Aufgabe [[Gelöste_Aufgaben/StaB|StaB]] ist | ||
::<math> | ::<math> | ||
\delta W^a = | \delta W^a = +\delta W_{4,0} \cdot F | ||
</math>. | </math>. | ||
Für <math>\delta \Pi</math> gilt | Für <math>\delta \Pi</math> gilt | ||
| Zeile 48: | Zeile 102: | ||
mit den virtuellen Formänderungsarbeiten der vier Stäbe. | mit den virtuellen Formänderungsarbeiten der vier Stäbe. | ||
Dabei haben wir Anteile der Arbeit aus der | Dabei haben wir Anteile der Arbeit aus der [https://numpedia.rzbt.haw-hamburg.de/index.php?title=Sources/Anleitungen/FEM-Formulierung_f%C3%BCr_den_Euler-Bernoulli-Balken Biegung] und der Längs-Dehnung des Stabes. | ||
Für den Stab ''k'' mit den Knoten ''I'' und ''J'' haben wir als Koodinaten der Knoten | Für den Stab ''k'' mit den Knoten ''I'' und ''J'' haben wir als Koodinaten der Knoten | ||
| Zeile 117: | Zeile 171: | ||
\end{pmatrix} | \end{pmatrix} | ||
</math> | </math> | ||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
/*-----------------------------------------------------*/ | |||
/* nodal coordinates */ | |||
nodalCoord : flatten(makelist([U[k,0],W[k,0],Φ[k,0]],k,1,4)); | |||
/*****************************************************/ | |||
/* Element-Striffness Matrix in local coordinates */ | |||
kI : (EI/ℓ[i]^3)*matrix([ 0, 0 , 0 , 0, 0 , 0 ], | |||
[ 0, 12 , 6*ℓ[i], 0, -12 , 6*ℓ[i]], | |||
[ 0,6*ℓ[i],4*ℓ[i]^2, 0,-6*ℓ[i],2*ℓ[i]^2], | |||
[ 0, 0 , 0 , 0, 0 , 0 ], | |||
[ 0, -12 , -6*ℓ[i], 0, 12 , -6*ℓ[i]], | |||
[ 0,6*ℓ[i],2*ℓ[i]^2, 0,-6*ℓ[i],4*ℓ[i]^2])+ | |||
(EA/ ℓ[i] )*matrix([ 1, 0 , 0 ,-1, 0 , 0 ], | |||
[ 0, 0 , 0 , 0, 0 , 0 ], | |||
[ 0, 0 , 0 , 0, 0 , 0 ], | |||
[-1, 0 , 0 , 1, 0 , 0 ], | |||
[ 0, 0 , 0 , 0, 0 , 0 ], | |||
[ 0, 0 , 0 , 0, 0 , 0 ]); | |||
</syntaxhighlight> | |||
}} | |||
<!--------------------------------------------------------------------------------> | |||
In den Ausdrücken der virtuellen Formänderungsenergie stehen die Koordinaten des lokalen Koordinatensystems von ''k''. Die müssen wir, wie in [ | {{MyCodeBlock|title=Transformation der Koordinaten in das globale System | ||
|text= | |||
In den Ausdrücken der virtuellen Formänderungsenergie stehen die Koordinaten des lokalen Koordinatensystems von ''k''. Die müssen wir, wie in Aufgabe [[Gel%C3%B6ste_Aufgaben/StaB|StaB]] mit der Euler-Drehmatrix ineinander überführen. | |||
Dafür haben wir | Dafür haben wir | ||
::<math> | ::<math> | ||
\left(\begin{array}{c}U_{I,0}\\W_{I,0}\\\Phi_{I,0}\end{array}\right) = | \left(\begin{array}{c}U_{I,0}\\W_{I,0}\\\Phi_{I,0}\end{array}\right) = | ||
\underline{\underline{D}}_R(\ | \underline{\underline{D}}_R(\alpha_k)\cdot | ||
\left(\begin{array}{c}U_{I,k}\\W_{I,k}\\\Phi_{I,k}\end{array}\right) | \left(\begin{array}{c}U_{I,k}\\W_{I,k}\\\Phi_{I,k}\end{array}\right) | ||
</math> | </math> | ||
mit der Transformationsmatrix | mit der Transformationsmatrix | ||
::<math> | ::<math> | ||
\underline{\underline{D}}_R(\ | \underline{\underline{D}}_R(\alpha_k) = | ||
\left(\begin{array}{c} \cos(\ | \left(\begin{array}{c} \cos(\alpha_k)& \sin(\alpha_k)& 0\\ | ||
-\sin(\ | -\sin(\alpha_k)& \cos(\alpha_k)& 0\\ | ||
0 & 0 & 1\end{array}\right) | 0 & 0 & 1\end{array}\right). | ||
</math> | |||
Es ist praktisch, an dieser Stelle die Abkürzung | |||
::<math> | |||
\underline{q}_{I,0} = \left(\begin{array}{c}U_{I,0}\\W_{I,0}\\\Phi_{I,0}\end{array}\right) | |||
</math> | </math> | ||
für die Koordinaten eines Knoten im Referenzsystem einzuführen. Also ist | |||
::<math> | ::<math> | ||
\underline{\underline{D}} | \left(\begin{array}{c}U_{I,k}\\W_{I,k}\\\Phi_{I,k}\end{array}\right) = \underline{\underline{D}}_R^T(\alpha_k)\cdot \underline{q}_{I,0} . | ||
\left(\begin{array}{ | </math> | ||
\underline{\underline{0}} & \underline{\underline{D}}^ | |||
Damit wir für die Elementsteifigkeitsmatrix - mit beiden Anfangs- und Endknoten des Elements - vom "0"-System ins "k"-System transformieren, brauchen wir die neue Transformations-Matrix | |||
::<math> | |||
\underline{\underline{T}}(\alpha_k) := | |||
\left(\begin{array}{cc} \underline{\underline{D}}_R^T(\alpha_k)& \underline{\underline{0}}\\ | |||
\underline{\underline{0}} & \underline{\underline{D}}_R^T(\alpha_k) | |||
\end{array}\right) | \end{array}\right) | ||
</math> | </math> | ||
Mit diesen | Mit diesen ist | ||
::<math> | ::<math> | ||
\delta\Pi = \sum_{k=1}^4 \delta \underline{Q}_{k,0}^T\cdot | \delta\Pi = \sum_{k=1}^4 \delta \underline{Q}_{k,0}^T\cdot | ||
\underbrace{ | \underbrace{ | ||
\underline{\underline{ | \underline{\underline{T}}^T(\alpha_k)\cdot | ||
\underline{\underline{K}}_{k,k}\cdot | \underline{\underline{K}}_{k,k}\cdot | ||
\underline{\underline{ | \underline{\underline{T}}(\alpha_k)}_{:= | ||
\underline{\underline{K}}_{k,0} }\cdot | \underline{\underline{K}}_{k,0} }\cdot | ||
\underline{Q}_{k,0} | \underline{Q}_{k,0} | ||
</math> | </math> | ||
Wir sammeln alle Koordianten der Knoten im ''0''-System in | Die resultierenden Element-Steifigkeitsmatrizen sind im folgenden aufgeschreiben: | ||
<math>\underline{Q}_{0}</math> und schreiben die Gleichgewichtsbedingungen in der Form | |||
<table class="wikitable mw-collapsible mw-collapsed" style="background-color:white; float: none; margin-right:14px;"> | |||
<tr><th>Element-Steigigkeitsmatrizen mit globalen Koordinaten</th></tr> | |||
<tr><th>Element #1</th></tr> | |||
<tr><td> | |||
<math> | |||
\underline{\underline{K}}_{1,0} = \begin{pmatrix}\frac{8 {{A}^{2}} E \eta }{{\ell_{0}^{3}}} & 0 & \frac{2 {{A}^{2}} E \eta }{{\ell_{0}^{2}}} & -\left( \frac{8 {{A}^{2}} E \eta }{{\ell_{0}^{3}}}\right) & 0 & \frac{2 {{A}^{2}} E \eta }{{\ell_{0}^{2}}}\\ | |||
0 & \frac{2 A E}{{\ell_0}} & 0 & 0 & -\left( \frac{2 A E}{{\ell_0}}\right) & 0\\ | |||
\frac{2 {{A}^{2}} E \eta }{{\ell_{0}^{2}}} & 0 & \frac{2 {{A}^{2}} E \eta }{3 {\ell_0}} & -\left( \frac{2 {{A}^{2}} E \eta }{{\ell_{0}^{2}}}\right) & 0 & \frac{{{A}^{2}} E \eta }{3 {\ell_0}}\\ | |||
-\left( \frac{8 {{A}^{2}} E \eta }{{\ell_{0}^{3}}}\right) & 0 & -\left( \frac{2 {{A}^{2}} E \eta }{{\ell_{0}^{2}}}\right) & \frac{8 {{A}^{2}} E \eta }{{\ell_{0}^{3}}} & 0 & -\left( \frac{2 {{A}^{2}} E \eta }{{\ell_{0}^{2}}}\right) \\ | |||
0 & -\left( \frac{2 A E}{{\ell_0}}\right) & 0 & 0 & \frac{2 A E}{{\ell_0}} & 0\\ | |||
\frac{2 {{A}^{2}} E \eta }{{\ell_{0}^{2}}} & 0 & \frac{{{A}^{2}} E \eta }{3 {\ell_0}} & -\left( \frac{2 {{A}^{2}} E \eta }{{\ell_{0}^{2}}}\right) & 0 & \frac{2 {{A}^{2}} E \eta }{3 {\ell_0}}\end{pmatrix} | |||
</math> | |||
</td></tr> | |||
<tr><th>Element #2</th></tr> | |||
<tr><td> | |||
<math> | |||
\underline{\underline{K}}_{2,0} = \begin{pmatrix}\frac{{{A}^{2}} E \eta +3 {\ell_{0}^{2}} A E}{4 {\ell_{0}^{3}}} & \frac{\sqrt{3} {{A}^{2}} E \eta -\sqrt{3} {\ell_{0}^{2}} A E}{4 {\ell_{0}^{3}}} & \frac{{{A}^{2}} E \eta }{4 {\ell_{0}^{2}}} & -\left( \frac{{{A}^{2}} E \eta +3 {\ell_{0}^{2}} A E}{4 {\ell_{0}^{3}}}\right) & -\left( \frac{\sqrt{3} {{A}^{2}} E \eta -\sqrt{3} {\ell_{0}^{2}} A E}{4 {\ell_{0}^{3}}}\right) & \frac{{{A}^{2}} E \eta }{4 {\ell_{0}^{2}}}\\ | |||
\frac{\sqrt{3} {{A}^{2}} E \eta -\sqrt{3} {\ell_{0}^{2}} A E}{4 {\ell_{0}^{3}}} & \frac{3 {{A}^{2}} E \eta +{\ell_{0}^{2}} A E}{4 {\ell_{0}^{3}}} & \frac{\sqrt{3} {{A}^{2}} E \eta }{4 {\ell_{0}^{2}}} & -\left( \frac{\sqrt{3} {{A}^{2}} E \eta -\sqrt{3} {\ell_{0}^{2}} A E}{4 {\ell_{0}^{3}}}\right) & -\left( \frac{3 {{A}^{2}} E \eta +{\ell_{0}^{2}} A E}{4 {\ell_{0}^{3}}}\right) & \frac{\sqrt{3} {{A}^{2}} E \eta }{4 {\ell_{0}^{2}}}\\ | |||
\frac{{{A}^{2}} E \eta }{4 {\ell_{0}^{2}}} & \frac{\sqrt{3} {{A}^{2}} E \eta }{4 {\ell_{0}^{2}}} & \frac{{{A}^{2}} E \eta }{3 {\ell_0}} & -\left( \frac{{{A}^{2}} E \eta }{4 {\ell_{0}^{2}}}\right) & -\left( \frac{\sqrt{3} {{A}^{2}} E \eta }{4 {\ell_{0}^{2}}}\right) & \frac{{{A}^{2}} E \eta }{6 {\ell_0}}\\ | |||
-\left( \frac{{{A}^{2}} E \eta +3 {\ell_{0}^{2}} A E}{4 {\ell_{0}^{3}}}\right) & -\left( \frac{\sqrt{3} {{A}^{2}} E \eta -\sqrt{3} {\ell_{0}^{2}} A E}{4 {\ell_{0}^{3}}}\right) & -\left( \frac{{{A}^{2}} E \eta }{4 {\ell_{0}^{2}}}\right) & \frac{{{A}^{2}} E \eta +3 {\ell_{0}^{2}} A E}{4 {\ell_{0}^{3}}} & \frac{\sqrt{3} {{A}^{2}} E \eta -\sqrt{3} {\ell_{0}^{2}} A E}{4 {\ell_{0}^{3}}} & -\left( \frac{{{A}^{2}} E \eta }{4 {\ell_{0}^{2}}}\right) \\ | |||
-\left( \frac{\sqrt{3} {{A}^{2}} E \eta -\sqrt{3} {\ell_{0}^{2}} A E}{4 {\ell_{0}^{3}}}\right) & -\left( \frac{3 {{A}^{2}} E \eta +{\ell_{0}^{2}} A E}{4 {\ell_{0}^{3}}}\right) & -\left( \frac{\sqrt{3} {{A}^{2}} E \eta }{4 {\ell_{0}^{2}}}\right) & \frac{\sqrt{3} {{A}^{2}} E \eta -\sqrt{3} {\ell_{0}^{2}} A E}{4 {\ell_{0}^{3}}} & \frac{3 {{A}^{2}} E \eta +{\ell_{0}^{2}} A E}{4 {\ell_{0}^{3}}} & -\left( \frac{\sqrt{3} {{A}^{2}} E \eta }{4 {\ell_{0}^{2}}}\right) \\ | |||
\frac{{{A}^{2}} E \eta }{4 {\ell_{0}^{2}}} & \frac{\sqrt{3} {{A}^{2}} E \eta }{4 {\ell_{0}^{2}}} & \frac{{{A}^{2}} E \eta }{6 {\ell_0}} & -\left( \frac{{{A}^{2}} E \eta }{4 {\ell_{0}^{2}}}\right) & -\left( \frac{\sqrt{3} {{A}^{2}} E \eta }{4 {\ell_{0}^{2}}}\right) & \frac{{{A}^{2}} E \eta }{3 {\ell_0}}\end{pmatrix} | |||
</math> | |||
</td></tr> | |||
<tr><th>Element #3</th></tr> | |||
<tr><td> | |||
<math> | |||
\underline{\underline{K}}_{3,0} = \begin{pmatrix}\frac{{{A}^{2}} E \eta +3 {\ell_{0}^{2}} A E}{4 {\ell_{0}^{3}}} & -\left( \frac{\sqrt{3} {{A}^{2}} E \eta -\sqrt{3} {\ell_{0}^{2}} A E}{4 {\ell_{0}^{3}}}\right) & \frac{{{A}^{2}} E \eta }{4 {\ell_{0}^{2}}} & -\left( \frac{{{A}^{2}} E \eta +3 {\ell_{0}^{2}} A E}{4 {\ell_{0}^{3}}}\right) & \frac{\sqrt{3} {{A}^{2}} E \eta -\sqrt{3} {\ell_{0}^{2}} A E}{4 {\ell_{0}^{3}}} & \frac{{{A}^{2}} E \eta }{4 {\ell_{0}^{2}}}\\ | |||
-\left( \frac{\sqrt{3} {{A}^{2}} E \eta -\sqrt{3} {\ell_{0}^{2}} A E}{4 {\ell_{0}^{3}}}\right) & \frac{3 {{A}^{2}} E \eta +{\ell_{0}^{2}} A E}{4 {\ell_{0}^{3}}} & -\left( \frac{\sqrt{3} {{A}^{2}} E \eta }{4 {\ell_{0}^{2}}}\right) & \frac{\sqrt{3} {{A}^{2}} E \eta -\sqrt{3} {\ell_{0}^{2}} A E}{4 {\ell_{0}^{3}}} & -\left( \frac{3 {{A}^{2}} E \eta +{\ell_{0}^{2}} A E}{4 {\ell_{0}^{3}}}\right) & -\left( \frac{\sqrt{3} {{A}^{2}} E \eta }{4 {\ell_{0}^{2}}}\right) \\ | |||
\frac{{{A}^{2}} E \eta }{4 {\ell_{0}^{2}}} & -\left( \frac{\sqrt{3} {{A}^{2}} E \eta }{4 {\ell_{0}^{2}}}\right) & \frac{{{A}^{2}} E \eta }{3 {\ell_0}} & -\left( \frac{{{A}^{2}} E \eta }{4 {\ell_{0}^{2}}}\right) & \frac{\sqrt{3} {{A}^{2}} E \eta }{4 {\ell_{0}^{2}}} & \frac{{{A}^{2}} E \eta }{6 {\ell_0}}\\ | |||
-\left( \frac{{{A}^{2}} E \eta +3 {\ell_{0}^{2}} A E}{4 {\ell_{0}^{3}}}\right) & \frac{\sqrt{3} {{A}^{2}} E \eta -\sqrt{3} {\ell_{0}^{2}} A E}{4 {\ell_{0}^{3}}} & -\left( \frac{{{A}^{2}} E \eta }{4 {\ell_{0}^{2}}}\right) & \frac{{{A}^{2}} E \eta +3 {\ell_{0}^{2}} A E}{4 {\ell_{0}^{3}}} & -\left( \frac{\sqrt{3} {{A}^{2}} E \eta -\sqrt{3} {\ell_{0}^{2}} A E}{4 {\ell_{0}^{3}}}\right) & -\left( \frac{{{A}^{2}} E \eta }{4 {\ell_{0}^{2}}}\right) \\ | |||
\frac{\sqrt{3} {{A}^{2}} E \eta -\sqrt{3} {\ell_{0}^{2}} A E}{4 {\ell_{0}^{3}}} & -\left( \frac{3 {{A}^{2}} E \eta +{\ell_{0}^{2}} A E}{4 {\ell_{0}^{3}}}\right) & \frac{\sqrt{3} {{A}^{2}} E \eta }{4 {\ell_{0}^{2}}} & -\left( \frac{\sqrt{3} {{A}^{2}} E \eta -\sqrt{3} {\ell_{0}^{2}} A E}{4 {\ell_{0}^{3}}}\right) & \frac{3 {{A}^{2}} E \eta +{\ell_{0}^{2}} A E}{4 {\ell_{0}^{3}}} & \frac{\sqrt{3} {{A}^{2}} E \eta }{4 {\ell_{0}^{2}}}\\ | |||
\frac{{{A}^{2}} E \eta }{4 {\ell_{0}^{2}}} & -\left( \frac{\sqrt{3} {{A}^{2}} E \eta }{4 {\ell_{0}^{2}}}\right) & \frac{{{A}^{2}} E \eta }{6 {\ell_0}} & -\left( \frac{{{A}^{2}} E \eta }{4 {\ell_{0}^{2}}}\right) & \frac{\sqrt{3} {{A}^{2}} E \eta }{4 {\ell_{0}^{2}}} & \frac{{{A}^{2}} E \eta }{3 {\ell_0}}\end{pmatrix} | |||
</math> | |||
</td></tr> | |||
<tr><th>Element #4</th></tr> | |||
<tr><td> | |||
<math> | |||
\underline{\underline{K}}_{4,0} = \begin{pmatrix}\frac{{{A}^{2}} E \eta }{{\ell_{0}^{3}}} & 0 & \frac{{{A}^{2}} E \eta }{2 {\ell_{0}^{2}}} & -\left( \frac{{{A}^{2}} E \eta }{{\ell_{0}^{3}}}\right) & 0 & \frac{{{A}^{2}} E \eta }{2 {\ell_{0}^{2}}}\\ | |||
0 & \frac{A E}{{\ell_0}} & 0 & 0 & -\left( \frac{A E}{{\ell_0}}\right) & 0\\ | |||
\frac{{{A}^{2}} E \eta }{2 {\ell_{0}^{2}}} & 0 & \frac{{{A}^{2}} E \eta }{3 {\ell_0}} & -\left( \frac{{{A}^{2}} E \eta }{2 {\ell_{0}^{2}}}\right) & 0 & \frac{{{A}^{2}} E \eta }{6 {\ell_0}}\\ | |||
-\left( \frac{{{A}^{2}} E \eta }{{\ell_{0}^{3}}}\right) & 0 & -\left( \frac{{{A}^{2}} E \eta }{2 {\ell_{0}^{2}}}\right) & \frac{{{A}^{2}} E \eta }{{\ell_{0}^{3}}} & 0 & -\left( \frac{{{A}^{2}} E \eta }{2 {\ell_{0}^{2}}}\right) \\ | |||
0 & -\left( \frac{A E}{{\ell_0}}\right) & 0 & 0 & \frac{A E}{{\ell_0}} & 0\\ | |||
\frac{{{A}^{2}} E \eta }{2 {\ell_{0}^{2}}} & 0 & \frac{{{A}^{2}} E \eta }{6 {\ell_0}} & -\left( \frac{{{A}^{2}} E \eta }{2 {\ell_{0}^{2}}}\right) & 0 & \frac{{{A}^{2}} E \eta }{3 {\ell_0}}\end{pmatrix} | |||
</math> | |||
</td></tr> | |||
</table> | |||
Wir sammeln nun alle Koordianten der Knoten im ''0''-System in | |||
::<math>\underline{Q}_{0}^T = \left(\underline{q}_{1,0}^T, \underline{q}_{2,0}^T, \underline{q}_{3,0}^T, \underline{q}_{4,0}^T \right)</math> | |||
und schreiben die Gleichgewichtsbedingungen in der Form | |||
::<math> | ::<math> | ||
\delta\underline{Q}_{0}^T\cdot\left(\underline{\underline{K}}_{0}\cdot\underline{Q}_{0} | \delta W = \delta\underline{Q}_{0}^T\cdot\left(\underline{\underline{K}}_{0}\cdot\underline{Q}_{0} | ||
- \underline{P}\right) = 0 | - \underline{P}\right) \stackrel{!}{=} 0 | ||
</math> | </math> | ||
an. | |||
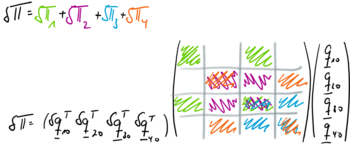
Dabei kommen die Beiträge zur Gesamt-Steifigkeitsmatrix (hier noch in der Fassung ohne Berücksichtigung der Randbedingungen) aus den vier Beiträgen der virtuellen Formänderungsenergie - die wir hier farblich gekennzeichnet haben: | |||
::[[Datei:StaF-11.png|350px|none|Einsortieren der Anteile der virtuellen Formänderungsenergie nach den Knoten.]] | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
/* apply transformation to global coordinates */ | |||
elemStiffMat: ratsimp(subst(params,makelist(transpose(DE(index[k][1])).subst(i=k,kI).DE(index[k][1]),k,1,4)))$ | |||
for i:1 thru 4 do | |||
print(k[i],"=",elemStiffMat[i])$ | |||
K: zeromatrix(length(nodalCoord),length(nodalCoord))$ | |||
for elem: 1 thru 4 do | |||
(pivot:append(3*(index[elem][2][1]-1)*[1,1,1], | |||
3*(index[elem][2][2]-1)*[1,1,1])+[1,2,3,1,2,3], | |||
for row: 1 thru 6 do | |||
for col: 1 thru 6 do | |||
K[pivot[row],pivot[col]] : K[pivot[row],pivot[col]]+elemStiffMat[elem][row,col])$ | |||
B: zeromatrix(length(nodalCoord),1)$ | |||
B[11,1]:F$ | |||
</syntaxhighlight> | |||
}} | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Einarbeitung der Randbedingungen | |||
|text= | |||
Die Randbedingungen arbeiten wir hier durch das Streichen der passenden Zeilen für <math>\delta U_{1,0},\delta W_{1,0},\delta U_{2,0},\delta W_{2,0}</math> sowie der passenden Spalten für <math>U_{1,0},W_{1,0},U_{2,0},W_{2,0}</math> ein. | |||
Das resultierende Gleichungssystem ist dies: | Das resultierende Gleichungssystem ist dies: | ||
| Zeile 174: | Zeile 337: | ||
\cdot | \cdot | ||
\begin{pmatrix} | \begin{pmatrix} | ||
{{\Phi }_{1,0}}\\ | {{\Phi }_{1,0}}\\ | ||
{{\Phi }_{2,0}}\\ | {{\Phi }_{2,0}}\\ | ||
{W_{3,0}}\\ | {W_{3,0}}\\ | ||
| Zeile 199: | Zeile 358: | ||
\end{pmatrix} | \end{pmatrix} | ||
</math> | </math> | ||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
/*-----------------------------------*/ | |||
/* boundary conditions */ | |||
K: submatrix(1,2,4,5,K,1,2,4,5)$ | |||
X: submatrix(1,2,4,5,transpose(nodalCoord))$ | |||
B: submatrix(1,2,4,5,B)$ | |||
print(K,"*",X,"=",B)$ | |||
</syntaxhighlight> | |||
}} | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Solving | |||
|text= | |||
Das Ergebnis ist - für die gleichen Parameter wie in Aufgabe [[Gel%C3%B6ste_Aufgaben/StaB|StaB]]: | |||
::<math> | ::<math> | ||
\begin{array}{l} | |||
U_{1,0}=0\\ | |||
W_{1,0}=0\\ | |||
\Phi_{1,0}=3.97 \frac{F}{E a^2}\\ | |||
U_{2,0}=0\\ | |||
W_{2,0}=0\\ | |||
\Phi_{2,0}=2.45 \frac{F}{E a^2}\\ | |||
U_{3,0}=57.7 \frac{F}{E a}\\ | |||
W_{3,0}=1.67\cdot 10^2 \frac{F}{E a}\\ | |||
\Phi_{3,0}=2.06 \frac{F}{E a^2}\\ | |||
U_{4,0}=-57.7 \frac{F}{E a}\\ | |||
W_{4,0}= 3.67\cdot 10^2 \frac{F}{E a}\\ | |||
\Phi_{4,0}=3.12 \frac{F}{E a^2} | |||
\end{array} | |||
</math> | </math> | ||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
/*-----------------------------------*/ | |||
/* solving */ | |||
sol: ratsimp(linsolve_by_lu(K,B)[1]); | |||
sol: append(makelist([U[1,0],W[1,0],U[2,0],W[2,0]][i]=0,i,1,4),makelist(X[i][1]=sol[i][1],i,1,length(X))); | |||
sol: makelist(nodalCoord[i]=subst(sol,nodalCoord[i]),i,1,length(nodalCoord)); | |||
fpprintprec: 3; | |||
print(transpose(float(subst(η=1,subst(moreParams,sol)))))$ | |||
</syntaxhighlight> | |||
}} | |||
<!--------------------------------------------------------------------------------> | <!--------------------------------------------------------------------------------> | ||
{{MyCodeBlock|title= | {{MyCodeBlock|title=Post-Processing | ||
|text= | |text= | ||
Mit diesen Ergebnissen können wir nun das Stabwerk in seiner verformten Konfiguration zeichnen. | |||
[[Datei:StaF-21.png|350px|right|mini|Stabwerk in verformter Konfiguration.]] | |||
Für die Darstellung müssen wir die Koodinaten der Verschiebung in die lokalen Koordinatensysteme zurücktransformieren - und das geht wieder über die Euler-Drehmatrizen (s.o.). | |||
Da die Koordinaten der Verschiebung im globalen Koordinatensystem die gleichen sind wie in Aufgabe [[Gelöste_Aufgaben/StaB|StaB]], sind auch die Verläufe der Schnittlasten in den Stäben identisch - wir brauchen also die Ergebnisse nicht noch einmal aufzutragen. | |||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
1+1 | /*-----------------------------------*/ | ||
/*-----------------------------------------------------*/ | |||
/* post-processing: show deformed structure */ | |||
/* employ these Trial-Functions - shared from FEM */ | |||
φ : [ (ξ-1)^2*(2*ξ+1), | |||
ℓ[i]* ξ *( ξ-1)^2, | |||
- ξ^2 *(2*ξ-3), | |||
ℓ[i]* ξ^2 *( ξ-1)]; | |||
/* construct u[i](x[i]),w[i](x[i]) */ | |||
/* step 1: re-construct local nodal-coordinates (DI(α))*/ | |||
/* step 2: use trial function to derive u[i],w[i] */ | |||
/* step 3: transform into global coordinates (DR(α)) */ | |||
sol: ratsimp(subst([η=1],subst(moreParams,sol)))$ | |||
fct:[]$ | |||
for e:1 thru 4 do | |||
(I: index[e][2][1], | |||
J: index[e][2][2], | |||
locals: [subst(params,matrix([U[I,e]],[W[I,e]],[Φ[I,e]])=DI(index[e][1]).matrix([U[I,0]],[W[I,0]],[Φ[I,0]])), | |||
subst(params,matrix([U[J,e]],[W[J,e]],[Φ[J,e]])=DI(index[e][1]).matrix([U[J,0]],[W[J,0]],[Φ[J,0]]))], | |||
trafo: flatten(makelist(makelist(lhs(locals[j])[i][1]=rhs(locals[j])[i][1],i,1,3),j,1,2)), | |||
/* ξ for x-Axis ..... */ | |||
localFct:matrix([ξ*ℓ[i]/ℓ[0] + U[I,e]*(1-ξ)+ U[J,e] *ξ ], | |||
[ W[I,e]*φ[1] + Φ[I,e]*φ[2]+W[J,e]*φ[3]+Φ[J,e]*φ[4]],[1]), | |||
localFct: subst(trafo,localFct), | |||
localFct: subst(params,subst([i=e],DR(index[e][1]).localFct)), | |||
fct: append(fct,[flatten(makelist(localFct[i],i,1,2))]))$ | |||
/* choose scale of deflection */ | |||
scale: [E=1000*F/a]; | |||
fct: float(expand(subst([scale],subst(moreParams,subst(params,subst(sol,fct)))))); | |||
/* and plot ..... */ | |||
toPlot: makelist([parametric, nodes[i][1] + fct[i][1], | |||
nodes[i][2] + fct[i][2], [ξ,0,1]],i,1,4); | |||
plot2d(toPlot, [legend,"Stab 1","Stab 2","Stab 3","Stab 4"]); | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
<hr/> | <hr/> | ||
'''Links''' | '''Links''' | ||
* | * * [[Gelöste_Aufgaben/StaB|Gelöste_Aufgaben / StaB]] | ||
'''Literature''' | '''Literature''' | ||
* ... | * ... | ||
Aktuelle Version vom 27. November 2024, 08:06 Uhr
Aufgabenstellung
Wir untersuchen die Belastung eines ebenen Stabwerks. Die Stäbe haben wie skizziert die Länge ℓ bzw. ℓ/2. Die Struktur wird mit der Kraft F belastet.
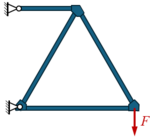
Gesucht ist ein Vergleich zwischen der klassischen Stabwerkstheorie und einer Herangehensweise, bei der wir eine feste Verbindung der Stäbe in den Knoten ansetzten. Grundlage des Modells ist die FEM-Lösung der Felddifferentialgleichung im Vergleich zur Lösung in Problemstellung „StaB“.
Wir stellen das Modell des Stabwerks mit dem Prinzip der virtuellen Verrückungen auf und vergleichen, wie sich diese von der Herangehensweise aus „Aufgabe StaB“ mit der analytischen Lösung unterscheidet.
Lösung mit Maxima
Wir nutzen das Computer-Algebra-System Maxima zur Lösung. Das macht hier Sinn, weil wir die Herangehensweise mit der aus Stab vergleichen wollen – für die wir ebenfalls Maxima eingesetzt haben.
Declarations
Wir übernehmen alle Vereinbarungen und Parameter aus der Problemformulierung „Stab“.
/*******************************************************/
/* MAXIMA script */
/* version: wxMaxima 21.05.2 */
/* author: Andreas Baumgart */
/* last updated: 2024-09-20 */
/* ref: NMM, Labor 2, dimensionsbehaftete */
/* Vorgehensweise */
/* description: finds the FEM solution for */
/* lab problem #2 */
/*******************************************************/
assume(A>0,H>h,h>0, a>0);
/*-----------------------------------------------------*/
/* Euler-Matrix */
DR(α) := matrix([ cos(α),sin(α), 0],
[-sin(α),cos(α), 0],
[ 0 , 0 , 1]);
/* inverse of Euler-Matrix */
DI(α) := transpose(DR(α));
/* compose transforation matrix for rod (two ends ....)*/
DE(α) := matrix([ cos(α),-sin(α), 0, 0 , 0 , 0],
[ sin(α), cos(α), 0, 0 , 0 , 0],
[ 0 , 0 , 1, 0 , 0 , 0],
[ 0 , 0 , 0, cos(α),-sin(α), 0],
[ 0 , 0 , 0, sin(α), cos(α), 0],
[ 0 , 0 , 0, 0 , 0 , 1]);
/* for each rod, define
* angle α, and
* node-IDs
at its start and end */
index : [[ 0 ,[1,3]], /* rod #1*/
[α[2],[2,3]], /* rod #2*/
[α[3],[3,4]], /* rod #3*/
[ 0 ,[2,4]] /* rod #4*/];
/* node - reference locations */
nodes: [[0,0],[0,sqrt(3)/2],[1/2,0],[0,sqrt(3)/2]]$
/*-----------------------------------------------------*/
/* system parameters */
params: [ℓ[1]=ℓ[0]/2, ℓ[2]=ℓ[0], ℓ[3]=ℓ[0], ℓ[4]=ℓ[0],
α[2]=%pi/3,α[3]= -%pi/3,
EA = E*A, EI = E*I, I=η*A^2/12];
moreParams: [A = a^2, ℓ[0]= 100*a];
Gleichgewichtsbedingungen
Für die Gleichgewichtsbedingung nach dem Prinzip der virtuellen Verrückungen
benötigen wir die virtuelle Formänderungsenergie und die virtuelle Arbeit der äußeren Kraft der äußeren Kräfte und Momente.
Mit den Konventionen für die Knoten-Verschiebungen aus Aufgabe StaB ist
- .
Für gilt
mit den virtuellen Formänderungsarbeiten der vier Stäbe.
Dabei haben wir Anteile der Arbeit aus der Biegung und der Längs-Dehnung des Stabes.
Für den Stab k mit den Knoten I und J haben wir als Koodinaten der Knoten
- und .
Damit haben wir
Für den Stab k definieren wir
- sowie
und finden damit
mit der Element-Steifigkeitsmatrix des Elements k im k-Koordinatensystem
/*-----------------------------------------------------*/
/* nodal coordinates */
nodalCoord : flatten(makelist([U[k,0],W[k,0],Φ[k,0]],k,1,4));
/*****************************************************/
/* Element-Striffness Matrix in local coordinates */
kI : (EI/ℓ[i]^3)*matrix([ 0, 0 , 0 , 0, 0 , 0 ],
[ 0, 12 , 6*ℓ[i], 0, -12 , 6*ℓ[i]],
[ 0,6*ℓ[i],4*ℓ[i]^2, 0,-6*ℓ[i],2*ℓ[i]^2],
[ 0, 0 , 0 , 0, 0 , 0 ],
[ 0, -12 , -6*ℓ[i], 0, 12 , -6*ℓ[i]],
[ 0,6*ℓ[i],2*ℓ[i]^2, 0,-6*ℓ[i],4*ℓ[i]^2])+
(EA/ ℓ[i] )*matrix([ 1, 0 , 0 ,-1, 0 , 0 ],
[ 0, 0 , 0 , 0, 0 , 0 ],
[ 0, 0 , 0 , 0, 0 , 0 ],
[-1, 0 , 0 , 1, 0 , 0 ],
[ 0, 0 , 0 , 0, 0 , 0 ],
[ 0, 0 , 0 , 0, 0 , 0 ]);
Transformation der Koordinaten in das globale System
In den Ausdrücken der virtuellen Formänderungsenergie stehen die Koordinaten des lokalen Koordinatensystems von k. Die müssen wir, wie in Aufgabe StaB mit der Euler-Drehmatrix ineinander überführen.
Dafür haben wir
mit der Transformationsmatrix
Es ist praktisch, an dieser Stelle die Abkürzung
für die Koordinaten eines Knoten im Referenzsystem einzuführen. Also ist
Damit wir für die Elementsteifigkeitsmatrix - mit beiden Anfangs- und Endknoten des Elements - vom "0"-System ins "k"-System transformieren, brauchen wir die neue Transformations-Matrix
Mit diesen ist
Die resultierenden Element-Steifigkeitsmatrizen sind im folgenden aufgeschreiben:
| Element-Steigigkeitsmatrizen mit globalen Koordinaten |
|---|
| Element #1 |
|
|
| Element #2 |
|
|
| Element #3 |
|
|
| Element #4 |
|
|
Wir sammeln nun alle Koordianten der Knoten im 0-System in
und schreiben die Gleichgewichtsbedingungen in der Form
an. Dabei kommen die Beiträge zur Gesamt-Steifigkeitsmatrix (hier noch in der Fassung ohne Berücksichtigung der Randbedingungen) aus den vier Beiträgen der virtuellen Formänderungsenergie - die wir hier farblich gekennzeichnet haben:
/* apply transformation to global coordinates */
elemStiffMat: ratsimp(subst(params,makelist(transpose(DE(index[k][1])).subst(i=k,kI).DE(index[k][1]),k,1,4)))$
for i:1 thru 4 do
print(k[i],"=",elemStiffMat[i])$
K: zeromatrix(length(nodalCoord),length(nodalCoord))$
for elem: 1 thru 4 do
(pivot:append(3*(index[elem][2][1]-1)*[1,1,1],
3*(index[elem][2][2]-1)*[1,1,1])+[1,2,3,1,2,3],
for row: 1 thru 6 do
for col: 1 thru 6 do
K[pivot[row],pivot[col]] : K[pivot[row],pivot[col]]+elemStiffMat[elem][row,col])$
B: zeromatrix(length(nodalCoord),1)$
B[11,1]:F$
Einarbeitung der Randbedingungen
Die Randbedingungen arbeiten wir hier durch das Streichen der passenden Zeilen für sowie der passenden Spalten für ein.
Das resultierende Gleichungssystem ist dies:
/*-----------------------------------*/
/* boundary conditions */
K: submatrix(1,2,4,5,K,1,2,4,5)$
X: submatrix(1,2,4,5,transpose(nodalCoord))$
B: submatrix(1,2,4,5,B)$
print(K,"*",X,"=",B)$
Solving
Das Ergebnis ist - für die gleichen Parameter wie in Aufgabe StaB:
/*-----------------------------------*/
/* solving */
sol: ratsimp(linsolve_by_lu(K,B)[1]);
sol: append(makelist([U[1,0],W[1,0],U[2,0],W[2,0]][i]=0,i,1,4),makelist(X[i][1]=sol[i][1],i,1,length(X)));
sol: makelist(nodalCoord[i]=subst(sol,nodalCoord[i]),i,1,length(nodalCoord));
fpprintprec: 3;
print(transpose(float(subst(η=1,subst(moreParams,sol)))))$
Post-Processing
Mit diesen Ergebnissen können wir nun das Stabwerk in seiner verformten Konfiguration zeichnen.
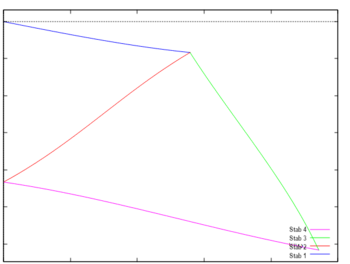
Für die Darstellung müssen wir die Koodinaten der Verschiebung in die lokalen Koordinatensysteme zurücktransformieren - und das geht wieder über die Euler-Drehmatrizen (s.o.).
Da die Koordinaten der Verschiebung im globalen Koordinatensystem die gleichen sind wie in Aufgabe StaB, sind auch die Verläufe der Schnittlasten in den Stäben identisch - wir brauchen also die Ergebnisse nicht noch einmal aufzutragen.
/*-----------------------------------*/
/*-----------------------------------------------------*/
/* post-processing: show deformed structure */
/* employ these Trial-Functions - shared from FEM */
φ : [ (ξ-1)^2*(2*ξ+1),
ℓ[i]* ξ *( ξ-1)^2,
- ξ^2 *(2*ξ-3),
ℓ[i]* ξ^2 *( ξ-1)];
/* construct u[i](x[i]),w[i](x[i]) */
/* step 1: re-construct local nodal-coordinates (DI(α))*/
/* step 2: use trial function to derive u[i],w[i] */
/* step 3: transform into global coordinates (DR(α)) */
sol: ratsimp(subst([η=1],subst(moreParams,sol)))$
fct:[]$
for e:1 thru 4 do
(I: index[e][2][1],
J: index[e][2][2],
locals: [subst(params,matrix([U[I,e]],[W[I,e]],[Φ[I,e]])=DI(index[e][1]).matrix([U[I,0]],[W[I,0]],[Φ[I,0]])),
subst(params,matrix([U[J,e]],[W[J,e]],[Φ[J,e]])=DI(index[e][1]).matrix([U[J,0]],[W[J,0]],[Φ[J,0]]))],
trafo: flatten(makelist(makelist(lhs(locals[j])[i][1]=rhs(locals[j])[i][1],i,1,3),j,1,2)),
/* ξ for x-Axis ..... */
localFct:matrix([ξ*ℓ[i]/ℓ[0] + U[I,e]*(1-ξ)+ U[J,e] *ξ ],
[ W[I,e]*φ[1] + Φ[I,e]*φ[2]+W[J,e]*φ[3]+Φ[J,e]*φ[4]],[1]),
localFct: subst(trafo,localFct),
localFct: subst(params,subst([i=e],DR(index[e][1]).localFct)),
fct: append(fct,[flatten(makelist(localFct[i],i,1,2))]))$
/* choose scale of deflection */
scale: [E=1000*F/a];
fct: float(expand(subst([scale],subst(moreParams,subst(params,subst(sol,fct))))));
/* and plot ..... */
toPlot: makelist([parametric, nodes[i][1] + fct[i][1],
nodes[i][2] + fct[i][2], [ξ,0,1]],i,1,4);
plot2d(toPlot, [legend,"Stab 1","Stab 2","Stab 3","Stab 4"]);
Links
Literature
- ...